Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Tony Shannon on ↑(39)
Editorial. Page i
On a generalization of dual-generalized complex Fibonacci quaternions
Original research paper. Pages 635–646
Elif Tan and Umut Öcal
Full paper (PDF, 199 Kb) | Abstract
In this study, we introduce a new class of generalized quaternions whose components are dual-generalized complex Horadam numbers. We investigate some algebraic properties of them.
New approaches of (q,k)-Fibonacci–Pell sequences via linear difference equations. Applications
Original research paper. Pages 647–669
Irene Magalhães Craveiro, Elen Viviani Pereira Spreafico and Mustapha Rachidi
Full paper (PDF, 317 Kb) | Abstract
In this paper we establish some explicit formulas of (q,k)-Fibonacci–Pell sequences via linear difference equations of order 2 with variable coefficients, and explore some of their new properties. More precisely, our results are based on two approaches, namely, the determinantal and the nested sums approaches, and their closed relations. As applications, we investigate the q-analogue Cassini identities and examine a pair of Rogers–Ramanujan type identities.
Identities for Fibonacci and Lucas numbers
Original research paper. Pages 670–681
George Grossman, Aklilu Zeleke and Xinyun Zhu
Full paper (PDF, 169 Kb) | Abstract
In this paper several new identities are given for the Fibonacci and Lucas numbers. This is accomplished by by solving a class of non-homogeneous, linear recurrence relations.
Almost balancers, almost cobalancers, almost Lucas-balancers and almost Lucas-cobalancers
Original research paper. Pages 682–694
Ahmet Tekcan and Esra Zeynep Türkmen
Full paper (PDF, 230 Kb) | Abstract
In this work, the general terms of almost balancers, almost cobalancers, almost Lucas-balancers and almost Lucas-cobalancers of first and second type are determined in terms of balancing and Lucas-balancing numbers. Later some relations on all almost balancing numbers and all almost balancers are obtained. Further the general terms of all balancing numbers, Pell numbers and Pell–Lucas number are determined in terms of almost balancers, almost Lucas-balancers, almost cobalancers and almost Lucas-cobalancers of first and second type.
On sums with generalized harmonic numbers via Euler’s transform
Original research paper. Pages 695–704
Neşe Ömür, Sibel Koparal and Laid Elkhiri
Full paper (PDF, 218 Kb) | Abstract
In this paper, we define the generalized hyperharmonic numbers of order

,
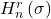
and get some identities involving these numbers by using Euler’s transform.
Perfect numbers, Wieferich primes and the solutions of 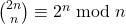
Original research paper. Pages 705–712
Gabriel Guedes and Ricardo Machado
Full paper (PDF, 302 Kb) | Abstract
In this article we focus on the solutions of a congruence equation:
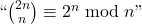
. Using the main result of this article and the SageMath software, we improve largely the number of known solutions. Furthermore, we prove that some famous numbers like even perfect numbers and Wieferich primes are connected to solutions of this equation.
Lower bounds on expressions dependent on functions φ(n), ψ(n) and σ(n)
Original research paper. Pages 713–716
Stoyan Dimitrov
Full paper (PDF, 247 Kb) | Abstract
The inequalities
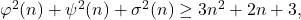
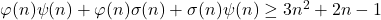
connecting
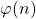
,
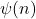
and
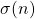
-functions are formulated and proved.
Note on the general monic quartic equation
Original research paper. Pages 717–723
Ioana Petkova
Full paper (PDF, 160 Kb) | Abstract
In this paper we present a new aproach for solving the general monic quartic equation. Moreover, we show that each quartic equation could be considered as a quasi-reciprocal equation, after a suitable translation of the variable.
Binary expansions of prime reciprocals
Original research paper. Pages 724–736
Brenda Navarro-Flores, José M. González-Barrios and Raúl Rueda
Full paper (PDF, 257 Kb) | Abstract
Prime numbers have been always of great interest. In this work, we explore the prime numbers from a sieve other than the Eratosthenes sieve. Given a prime number

, we consider the binary expansion of
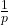
and, in particular, the size of the period of
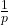
. We show some results that relate the size of the period to properties of the prime numbers.
The 2-adic valuation of the general degree-2 polynomial in 2 variables
Original research paper. Pages 737–751
Shubham
Full paper (PDF, 264 Kb) | Abstract
We define the

-adic valuation tree of a polynomial
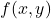
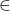
![Rendered by QuickLaTeX.com \mathbb{Z}[x,y]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-9d11f1f3256245b0abc739e0dfea7ece_l3.png)
by which we can find its

-adic valuation at any point. This work includes diverse
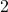
-adic valuation trees of certain degree-two polynomials in two variables. Among these, the
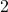
-adic valuation tree of
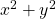
is most interesting. We use the observations from these trees to study the
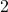
-adic valuation tree of the general degree-two polynomial in
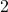
variables. We also study the
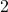
-adic valuation tree of the polynomial
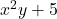
.
Notes on generalized and extended Leonardo numbers
Original research paper. Pages 752–773
Anthony G. Shannon, Peter J.-S. Shiue and Shen C. Huang
Full paper (PDF, 359 Kb) | Abstract
This paper both extends and generalizes recently published properties which have been developed by many authors for elements of the Leonardo sequence in the context of second-order recursive sequences. It does this by considering the difference equation properties of the homogeneous Fibonacci sequence and the non-homogeneous properties of their Leonardo sequence counterparts. This produces a number of new identities associated with a generalized Leonardo sequence and its associated algorithm, as well as some combinatorial results which lead into elegant properties of hyper-Fibonacci numbers in contrast to their ordinary Fibonacci number analogues, and as a convolution of Fibonacci and Leonardo numbers.
n-Rooks and n-queens problem on planar and modular chessboards with hexagonal cells
Original research paper. Pages 774–788
Eduard C. Taganap and Rainier D. Almuete
Full paper (PDF, 2044 Kb) | Abstract
We show the existence of solutions to the

-rooks problem and

-queens problem on chessboards with hexagonal cells, problems equivalent to certain three and six direction riders on ordinary chessboards. Translating the problems into graph theory problems, we determine the independence number (maximum size of independent set) of rooks graph and queens graph. We consider the

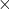

planar diamond-shaped H

with hexagonal cells, and the board H

as a flat torus T

. Here, a rook can execute moves on lines perpendicular to the six sides of the cell it is placed, and a queen can execute moves on those lines together with lines through the six corners of the cell it is placed.
New Fibonacci-type pulsated sequences
Original research paper. Pages 789–793
Lilija Atanassova and Velin Andonov
Full paper (PDF, 165 Kb) | Abstract
In this paper, we define generalized hyperharmonic numbers of order
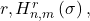
for
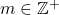
and give some applications by using generating functions of these
numbers. For example, for
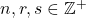
such that
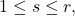
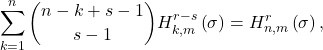
and
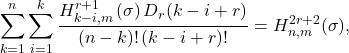
where 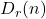 is an
is an  -derangement number.
-derangement number.
The Wiener, hyper-Wiener, Harary and SK indices of the P(Zpk·qr) power graph
Original research paper. Pages 794–803
Volkan Aşkin
Full paper (PDF, 758 Kb) | Abstract
The undirected
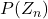
power graph of a finite group of
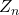
is a connected graph, the set of vertices of which is
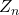
. Here
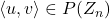
are two diverse adjacent vertices if and only if
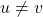
and
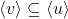
or
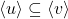
. We will shortly name the undirected
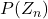
power graph as the power graph
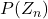
. The Wiener, hyper-Wiener, Harary and SK indices of the
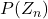
power graph are in order as follows
![Rendered by QuickLaTeX.com \[\frac{1}{2}\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,d\left( u,v \right), \ \frac{1}{2}\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,d\left( u,v \right)+\frac{1}{2}\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,{{d}^{2}}\left(u,v \right),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-79cfee7d98565f67478202080da96c58_l3.png)
![Rendered by QuickLaTeX.com \[\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,\frac{1}{d\left(u,v \right)} \mbox{ and } \frac{1}{2}\underset{uv\in E\left( G \right)}{\mathop \sum }\,\left( {{d}_{u}}+{{d}_{v}} \right).\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-8805061951a956fe39350c7bd8147e44_l3.png)
In this article we focus more on the indices of 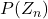 power graph by Wiener, hyper-Wiener, Harary and SK the definition of the power graph is presented and the results and theorems which we need in our discussion are provided in the introduction. Finally, the main point of the article is that we calculate the Wiener, hyper-Wiener, Harary and SK indices of the power graph
power graph by Wiener, hyper-Wiener, Harary and SK the definition of the power graph is presented and the results and theorems which we need in our discussion are provided in the introduction. Finally, the main point of the article is that we calculate the Wiener, hyper-Wiener, Harary and SK indices of the power graph 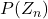 corresponding to the vertex
corresponding to the vertex 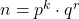 . These are as follows:
. These are as follows: 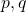 are distinct primes and
are distinct primes and 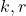 are nonnegative integers.
are nonnegative integers.
On generalized hyperharmonic numbers of order 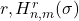
Original research paper. Pages 804–812
Sibel Koparal, Neşe Ömür and Laid Elkhiri
Full paper (PDF, 282 Kb) | Abstract
In this paper, we define generalized hyperharmonic numbers of order
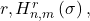
for
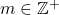
and give some applications by using generating functions of these
numbers. For example, for
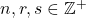
such that
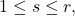
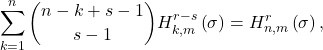
and
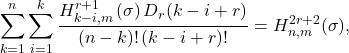
where 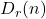 is an
is an  -derangement number.
-derangement number.
On a modification of Set(n)
Original research paper. Pages 813–819
Krassimir T. Atanassov and József Sándor
Full paper (PDF, 300 Kb) | Abstract
A modification of the set
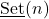
for a fixed natural number

is introduced in the form:
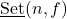
, where
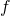
is an arithmetic function. The sets
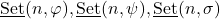
are discussed, where
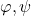
and
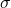
are Euler’s function, Dedekind’s function and the sum of the positive divisors of

, respectively.
Nontrivial lower bounds for the p-adic valuations of some type of rational numbers and an application for establishing the integrality of some rational sequences
Original research paper. Pages 820–826
Bakir Farhi
Full paper (PDF, 228 Kb) | Abstract
In this note, based on a certain functional equation of the dilogarithm function, we establish nontrivial lower bounds for the p-adic valuation (where p is a given prime number) of some type of rational numbers involving harmonic numbers. Then we use our estimate to derive the integrality of some sequences of rational numbers, which cannot be seen directly from their definitions.
The t-Fibonacci sequences in the 2-generator p-groups of nilpotency class 2
Original research paper. Pages 827–841
Elahe Mehraban, Ömur Deveci and Evren Hincal
Full paper (PDF, 320 Kb) | Abstract
In this paper, we consider the 2-generator p-groups of nilpotency class 2. We will discuss the lengths of the periods of the t-Fibonacci sequences in these groups.
Some geometric properties of the Padovan vectors in Euclidean 3-space
Original research paper. Pages 842–860
Serdar Korkmaz and Hatice Kuşak Samancı
Full paper (PDF, 743 Kb) | Abstract
Padovan numbers were defined by Stewart (1996) in honor of the modern architect Richard Padovan (1935) and were first discovered in 1924 by Gerard Cordonnier. Padovan numbers are a special status of Tribonacci numbers with initial conditions and general terms. The ratio between Padovan numbers is one of the important algebraic numbers because it produces plastic numbers. Up to now, various studies have been conducted on Padovan numbers and Padovan polynomial sequences. In this study, Padovan vectors are defined for the first time by using the Padovan Binet-like formula and reduction relation. Then, geometric properties of Padovan vectors such as inner product, norm, and vector products are analyzed. In the last part of the study, Padovan vectors were calculated with Binet formulas in the Geogebra program. In addition, the first ten Padovan numbers and Padovan vectors were calculated using the Binet formulas and shown as points and vectors in three-dimensional space. According to the Padovan vectors found, the Padovan curve was drawn in space for the first time by using the curve fitting feature of the Geogebra program. Thus, with our study, a geometric approach to Padovan number sequences was brought for the first time.
On tertions and other algebraic objects
Original research paper. Pages 861–880
Krassimir T. Atanassov
Full paper (PDF, 267 Kb) | Abstract
The concept of the object called “tertion” is discussed. Some operations over tertions are introduced and their properties are studied. The relationship between tertions, complex numbers are quaternions are discussed.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP4/30/2022.
Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]()
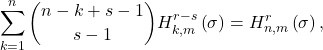
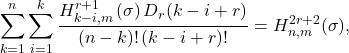
![]() is an
is an ![]() -derangement number.
-derangement number.![Rendered by QuickLaTeX.com \[\frac{1}{2}\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,d\left( u,v \right), \ \frac{1}{2}\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,d\left( u,v \right)+\frac{1}{2}\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,{{d}^{2}}\left(u,v \right),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-79cfee7d98565f67478202080da96c58_l3.png)
![Rendered by QuickLaTeX.com \[\underset{\left\{ u,v \right\}\subseteq V\left( G \right)}{\mathop \sum }\,\frac{1}{d\left(u,v \right)} \mbox{ and } \frac{1}{2}\underset{uv\in E\left( G \right)}{\mathop \sum }\,\left( {{d}_{u}}+{{d}_{v}} \right).\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-8805061951a956fe39350c7bd8147e44_l3.png)
![]() power graph by Wiener, hyper-Wiener, Harary and SK the definition of the power graph is presented and the results and theorems which we need in our discussion are provided in the introduction. Finally, the main point of the article is that we calculate the Wiener, hyper-Wiener, Harary and SK indices of the power graph
power graph by Wiener, hyper-Wiener, Harary and SK the definition of the power graph is presented and the results and theorems which we need in our discussion are provided in the introduction. Finally, the main point of the article is that we calculate the Wiener, hyper-Wiener, Harary and SK indices of the power graph ![]() corresponding to the vertex
corresponding to the vertex ![]() . These are as follows:
. These are as follows: ![]() are distinct primes and
are distinct primes and ![]() are nonnegative integers.
are nonnegative integers.![]()
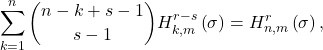
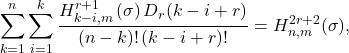
![]() is an
is an ![]() -derangement number.
-derangement number.

