Notes on generalized and extended Leonardo numbers

Anthony G. Shannon, Peter J.-S. Shiue and Shen C. Huang
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 751–773
DOI: 10.7546/nntdm.2023.29.4.752-773
Full paper (PDF, 359 Kb)

Details

Authors and affiliations

Anthony G. Shannon
Warrane College, University of New South Wales
Kensington, NSW 2033, Australia

Peter J.-S. Shiue
Department of Mathematical Sciences, University of Nevada, Las Vegas
4505 S Maryland Pkwy, Las Vegas, NV 89154, USA

Shen C. Huang
Department of Mathematical Sciences, University of Nevada, Las Vegas
4505 S Maryland Pkwy, Las Vegas, NV 89154, USA

Abstract

This paper both extends and generalizes recently published properties which have been developed by many authors for elements of the Leonardo sequence in the context of second-order recursive sequences. It does this by considering the difference equation properties of the homogeneous Fibonacci sequence and the non-homogeneous properties of their Leonardo sequence counterparts. This produces a number of new identities associated with a generalized Leonardo sequence and its associated algorithm, as well as some combinatorial results which lead into elegant properties of hyper-Fibonacci numbers in contrast to their ordinary Fibonacci number analogues, and as a convolution of Fibonacci and Leonardo numbers.

Keywords

• Binet formulas
• Leonardo sequences
• Generalized Leonardo sequence
• Extended Leonardo sequence
• Fibonacci sequences
• Hyper-Fibonacci sequences
• Recurrence relations
• Undetermined coefficients

2020 Mathematics Subject Classification

• 05A19
• 11B37
• 11B39

References

1. Alp, Y. (2023). Hybrid hyper-Fibonacci and hyper-Lucas numbers. Notes on Number Theory and Discrete Mathematics, 29(1), 154–170.
2. Bahs¸i, M. & Solak, S. (2016). A symmetric algorithm for golden ratio in hyper-Horadam numbers. Chinese Journal of Mathematics, Article ID 4361582.
3. Bicknell-Johnson, M.& Bergum, G. E. (1988). The generalized Fibonacci numbers 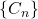, 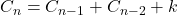. Applications of Fibonacci Numbers: Proceedings of The Second International Conference on Fibonacci Numbers and Their Applications. San Jose State University, California, USA, Springer, 193–205.
4. Catarino, P. M., & Borges, A. (2019). On Leonardo Numbers. Acta Mathematica
   Universitatis Comenianae, 89(1), 75–86.
5. Chu, H. V., Irmak, N., Miller, S. J., Szalay, L., & Zhang, S. X. Schreier multisets and the s-step Fibonacci sequences (in press)
6. Dil, A., & Mező, I. (2008). A symmetric algorithm for hyperharmonic and Fibonacci numbers. Applied Mathematics and Computation, 206(2), 942–951.
7. He, T.-X., & Shiue, P. J.-S. (2009). On sequences of numbers and polynomials defined by linear recurrence relations of order 2. International Journal of Mathematics and Mathematical Sciences, 21, Article ID 709386.
8. Horadam, A. F. (1966). Generalization of two theorems of K. Subba Rao. Bulletin of Calcutta Mathematical Society, 58(1), 23–29.
9. Horadam, A. F. (1965). Basic properties of a certain generalized sequence of numbers. The Fibonacci Quarterly, 3(3), 161–176.
10. Jarden, D. (1996). Recurring Sequences. Jerusalem: Riveon Lematematika, 95–102.
11. Komatsu, T.,& Szalay, L. (2018). A new formula for hyper-Fibonacci numbers, and the number of occurrences. Turkish Journal of Mathematics, 42(3), 993–1004.
12. Koshy, T. (2019). Fibonacci and Lucas Numbers with Applications (Volume 2), John Wiley & Sons.
13. Kuhapatanakul, K., & Chobsorn, J. (2022). On the generalized Leonardo numbers. Integers, 22, A48.
14. Lind, D. A. (1965). On a class of non-linear binomial sums. The Fibonacci Quarterly, 3(4), 292–298.
15. Ollerton, R. L., & Shannon, A. G. (1998). Some Properties of Generalized Pascal Squares and Triangles. The Fibonacci Quarterly, 36(2), 98–109.
16. Shannon, A. G. (1977). Tribonacci numbers and Pascal’s pyramid. The Fibonacci Quarterly, 15(3), 268–275.
17. Shannon, A. G. (2019). A note on generalized Leonardo numbers. Notes on Number Theory and Discrete Mathematics, 25(3), 97–101.
18. Shannon, A. G., & Deveci, Ö. (2022). A note on generalized and extended Leonardo sequences. Notes on Number Theory and Discrete Mathematics, 28(1), 109–114.
19. Shattuck, M. (2022). Combinatorial proofs of identities for the generalized Leonardo numbers. Notes on Number Theory and Discrete Mathematics, 28(4), 778–790.

Manuscript history

• Received: 19 September 2023
• Accepted: 30 October 2023
• Online First: 27 November 2023

Copyright information

Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).