Shubham
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 737–751
DOI: 10.7546/nntdm.2023.29.4.737-751
Full paper (PDF, 264 Kb)
Details
Authors and affiliations
Shubham ![]()
![]()
School of Physical Sciences, Jawaharlal Nehru University
New Delhi, India
Abstract
We define the ![]() -adic valuation tree of a polynomial
-adic valuation tree of a polynomial ![]()
![]()
![]() by which we can find its
by which we can find its ![]() -adic valuation at any point. This work includes diverse
-adic valuation at any point. This work includes diverse ![]() -adic valuation trees of certain degree-two polynomials in two variables. Among these, the
-adic valuation trees of certain degree-two polynomials in two variables. Among these, the ![]() -adic valuation tree of
-adic valuation tree of ![]() is most interesting. We use the observations from these trees to study the
is most interesting. We use the observations from these trees to study the ![]() -adic valuation tree of the general degree-two polynomial in
-adic valuation tree of the general degree-two polynomial in ![]() variables. We also study the
variables. We also study the ![]() -adic valuation tree of the polynomial
-adic valuation tree of the polynomial ![]() .
.
Keywords
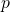 -adic valuation
-adic valuation- Valuation tree
- Polynomial sequences
2020 Mathematics Subject Classification
- 11B99
- 11D88
- 11B83
References
- Amdeberhan, T., De Angelis, V., & Moll, V. H. (2013). Complementary Bell numbers: Arithmetical properties and Wilf’s conjecture. Advances in Combinatorics, 23–56, Springer.
- Amdeberhan, T., Manna, D., & Moll, V. H. (2008). The 2-adic valuation of Stirling numbers. Experimental Mathematics, 17, 69–82.
- Berribeztia, A., Medina, L., Moll, A., Moll, V., & Noble, L. (2010). The p-adic valuation of Stirling numbers. Journal for Algebra and Number Theory Academia, 1, 1–30.
- Borwein, J. M., & Crandall, R. (2013). Closed forms: what they are and why we care. Notices of The American Mathematical Society, 60, 50–65.
- Brucal–Hallare, M., Goedhart, E. G., Riley, R. M., Sharma, V., & Thompson, B. (2021). Solving quadratic and cubic Diophantine equations using 2-adic valuation trees. Available online at: https://doi.org/10.48550/arXiv.2105.03352.
- Byrnes, A., Fink, J., Lavigne, G., Nogues, I., Rajasekaran, S., Yuan, A., Almodovar, L., Guan, X., Kesarwani, A., Medina, L., Rowland, E., & Moll, V. H. (2019). A closed-form solution might be given by a tree. Valuations of quadratic polynomials. Scientia, Series A: Mathematical Sciences, 29 11–28.
- Caicedo, J. B., Moll, V. H., Ram´ırez, J. L., & Villamizar, D. (2019). Extensions of set partitions and permutations. Electronic Journal of Combinatorics, 26(2), Article Number P2.20.
- Chow, T. Y. (1999). What is a closed-form number? American Mathematical Monthly, 106(5), 440–448.
- Conrad, K. A multivariable Hensel’s lemma. Available online at: https://kconrad.
math.uconn.edu/blurbs/gradnumthy/multivarhensel.pdf. - Gouvêa, F. Q. (2020). p-adic Numbers: An Introduction (Universitext). (3rd ed.). Springer.
- Legendre, A. M. (1830). Théorie des Nombres. Firmin Didot Freres, Paris.
- Sun, X., & Moll, V. H. (2010). A binary tree representation for the 2-adic valuation of a sequence arising from a rational integral. Integers, 10(2), 211–222.
Manuscript history
- Received: 1 February 2023
- Revised: 14 October 2023
- Accepted: 25 November 2023
- Online First: 26 November 2023
Copyright information
![]() Ⓒ 2023 by the Author.
Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Shubham (2023). The 2-adic valuation of the general degree-2 polynomial in 2 variables. Notes on Number Theory and Discrete Mathematics, 29(4), 737-751, DOI: 10.7546/nntdm.2023.29.4.737-751.


