Volume 31 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
The quaternion-type cyclic-balancing sequence in groups
Original research paper. Pages 201–210
Nazmiye Yılmaz, Esra Kırmızı Çetinalp and Ömür Deveci
Full paper (PDF, 232 Kb) | Abstract
In this research, several types of definitions of the quaternion-type cyclic-balancing sequence are presented. The Cassini formula and generating function of these sequences are also obtained for all types. The quaternion-type cyclic-balancing sequences modulo
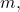
the first step to transferring this topic to group theory, are examined. These sequences in finite groups are then defined. Eventually, the lengths of periods for these sequences of the generalized quaternion group are calculated.
A new approach to tridiagonal matrices related to the Sylvester–Kac matrix
Original research paper. Pages 211–227
Efruz Özlem Mersin and Mustafa Bahşi
Full paper (PDF, 307 Kb) | Abstract
The Sylvester–Kac matrix, a well-known tridiagonal matrix, has been extensively studied for over a century, with various generalizations explored in the literature. This paper introduces a new type of tridiagonal matrix, where the matrix entries are defined by an integer sequence, setting it apart from the classical Sylvester–Kac matrix. The aim of this paper is to investigate several fundamental properties of this generalized matrix, including its algebraic structure, determinant, inverse, LU decomposition, characteristic polynomial, and various norms.
Alternative solutions to the Legendre’s equation 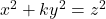
Original research paper. Pages 228–235
Kanwara Mukkhata and Sompong Chuysurichay
Full paper (PDF, 243 Kb) | Abstract
In this paper, we aim to provide alternative solutions of the Legendre’s equation
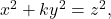
where

is a square-free positive integer. The results also lead to solutions of the well-known Pythagorean triples and Eisenstein triples.
Bivariate Leonardo polynomials and Riordan arrays
Original research paper. Pages 236–250
Yasemin Alp and E. Gökçen Koçer
Full paper (PDF, 234 Kb) | Abstract
In this paper, bivariate Leonardo polynomials are defined, which are closely related to bivariate Fibonacci polynomials. Bivariate Leonardo polynomials are generalizations of the Leonardo polynomials and Leonardo numbers. Some properties and identities (Cassini, Catalan, Honsberger, d’Ocagne) for the bivariate Leonardo polynomials are obtained. Then, the Riordan arrays are defined by using bivariate Leonardo polynomials.
Elementary proof of W. Schulte’s conjecture
Original research paper. Pages 251–255
Djamel Himane
Full paper (PDF, 187 Kb) | Abstract
In the On-Line Encyclopedia of Integer Sequences, we find the sequence
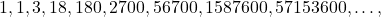
which is given by the formula
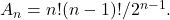
On the same page, Werner Schulte conjectured that for all
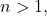

divides
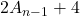
if and only if

is prime. In this paper, we employ elementary methods to provide a simple proof of this conjecture.
Common values of two k-generalized Pell sequences
Original research paper. Pages 256–268
Zafer Şiar, Florian Luca and Faith Shadow Zottor
Full paper (PDF, 275 Kb) | Abstract
Let
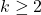
and let
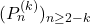
be the

-generalized Pell sequence defined by
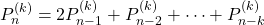
for 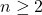 with initial conditions
with initial conditions
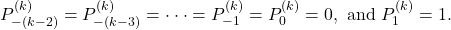
In this study, we look at the equation 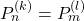 in positive integers
in positive integers 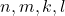 such that
such that 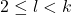 and show that it has only trivial solution, namely
and show that it has only trivial solution, namely 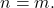
An algorithm for complex factorization of the bi-periodic Fibonacci and Lucas polynomials
Original research paper. Pages 269–279
Baijuan Shi and Can Kızılateş
Full paper (PDF, 225 Kb) | Abstract
In this paper, we consider the factorization of generalized sequences, by employing a method based on trigonometric identities. The new method is of reduced complexity and represents an improvement compared to existing results. We establish a connection between the bi-periodic Fibonacci and Lucas polynomials and tridiagonal matrices, which exploits the calculation of eigenvalues of associated tridiagonal matrices.
Weighted sum of the sixth powers of Horadam numbers
Original research paper. Pages 280–288
Kunle Adegoke, Chiachen Hsu and Olawanle Layeni
Full paper (PDF, 175 Kb) | Abstract
Ohtsuka and Nakamura found simple formulas for
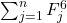
and
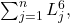
where
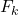
and
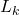
are the

-th Fibonacci and Lucas numbers, respectively. In this note we extend their results to a general second order sequence by deriving a formula for
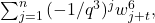
where
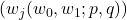
is the Horadam sequence defined by
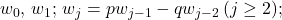
where
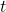
is an arbitrary integer and
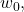
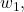

and
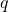
are arbitrary complex numbers, with
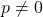
and
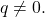
As a by-product we establish a divisibility property for the generalized Fibonacci sequence.
Identical equations for multiplicative functions
Original research paper. Pages 289–298
Pentti Haukkanen
Full paper (PDF, 210 Kb) | Abstract
We examine identical equations for multiplicative functions and certain special cases, such as totients and quadratics. We confine ourselves to identical equations expressing the value
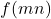
(or the value
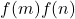
) nontrivially in terms of the values
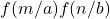
and
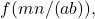
where
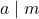
and
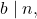
and holding for all
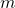
and
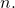
Particular attention is paid to Busche–Ramanujan type identities. We characterize all functions that satisfy the identical equations. Quasi-multiplicative functions are central to this discussion.
On an inequality about Euler’s totient function
Original research paper. Pages 299–304
Cheng-Ting Wang
Full paper (PDF, 273 Kb) | Abstract
In this paper, we show that when
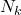
is a primorial and
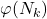
is Euler’s totient function, the inequality
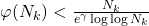
holds for all positive integer
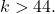
On arithmetic Heilbronn supercharacters
Original research paper. Pages 305–310
Mircea Cimpoeaș
Full paper (PDF, 197 Kb) | Abstract
In this note, we introduce arithmetic Heilbronn supercharacters that generalize the notions of arithmetic Heilbronn characters and Heilbronn supercharacters and discuss several properties of them.
On the generalized p-periodic linear recursive sequences via the Fibonacci–Horner decomposition of the matrix powers
Original research paper. Pages 311–325
Mustapha Rachidi, László Szalay and Fatih Yilmaz
Full paper (PDF, 293 Kb) | Abstract
In this study, we investigate the matrix formulation of the generalized

-periodic linear recursive sequences. To reach our goal, we consider the properties of the Fibonacci–Horner decomposition of the matrix powers and those of the weighted linear recursive sequence of Fibonacci type. We provide the linear, the combinatorial, and the analytic representations of the generalized

-periodic linear recursive sequences. For illustrating our general results, properties of some special cases are studied and numerical example are furnished.
Floor and ceiling functions for Pell numbers
Original research paper. Pages 326–334
İsmail Sulan and Mustafa Aşçı
Full paper (PDF, 201 Kb) | Abstract
The analytical study of the Pell number and the role of floor and ceiling functions into their computation is examined. Closed expressions of Pell numbers were initially derived using Binet’s formula, followed by an asymptotic behavior study of the sequence using this formula. Taking into account the decreasing trend in the term
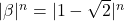
for large values of

, a formula that closely approximates Pell numbers has been developed. In this context, relationships between numbers are clarified using floor and ceiling functions. The accuracy with which various theorems and lemmas mathematically prove these approximations is also included. The study also looks at limit processes with emphasis placed upon the determining influence that the ratio
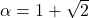
has on the growth rate of the sequence.
Two Fibonacci-like sequences
Original research paper. Pages 335–339
Krassimir T. Atanassov and Anthony G. Shannon
Full paper (PDF, 135 Kb) | Abstract
In the present paper we will discuss the two Fibonacci-like sequences
![Rendered by QuickLaTeX.com \[ s_{2k+1} = s_{2k} - s_{2k-1} + \cdots - s_1 + s_0\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-1974fa426f79c58a4c06d7c471ecd11f_l3.png)
with 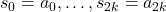 and
and
![Rendered by QuickLaTeX.com \[s_{2k+2} = s_{2k+1} - s_{2k} + \cdots + s_1 - s_0\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-12045a4fe5a973ff40147347f68407dc_l3.png)
with 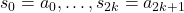 , where
, where 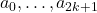 are arbitrary numbers.
are arbitrary numbers.
Examples and explicit formulas for 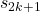 and
and 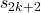 are given.
are given.
On robust multiplication method for higher even-dimensional rhotrices
Original research paper. Pages 340–360
A. O. Isere and T. O. Utoyo
Full paper (PDF, 269 Kb) | Abstract
Rhotrices (heart-oriented) are often multiplied either by heart-based or row-column multiplication method. The element-wise multiplication method for higher even-dimensional rhotrices has recently been introduced in [9]. However, this type of multiplication method, though simple, is less robust. Hence, we present a multiplication method called “Robust Multiplication Method” (RMM) for higher even-dimensional rhotrices (hl-rhotrices), and a number of rediscovered properties of hl-rhotrices. Analysis and examples of RMM for some hl-rhotrices are presented for demonstration purposes.
On certain inequalities for φ, ψ, σ and related functions, III
Original research paper. Pages 361–369
József Sándor and Karol Gryszka
Full paper (PDF, 193 Kb) | Abstract
We obtain generalizations of certain results from [2] and [4]. The unitary variants are also considered. Some new arithmetic functions and their inequalities are also considered.
Non-Fisherian generalized Fibonacci numbers
Original research paper. Pages 370–389
Thor Martinsen
Full paper (PDF, 283 Kb) | Abstract
Using biology as inspiration, this paper explores a generalization of the Fibonacci sequence that involves gender biased sexual reproduction. The female, male, and total population numbers along with their associated recurrence relations are considered. We demonstrate that the generalized Fibonacci numbers being investigated are generalized third order Pell–Lucas numbers. Sequence properties, generating functions, and closed-form solutions for these new generalized Fibonacci numbers, as well as several identities involving Jacobsthal, Leonardo, and generalized Leonardo numbers are presented. The generalized Fibonacci number framework developed gives rise to many previously uncataloged sequences, and develops new connections between known sequences.
Almost repdigits in balancing and Lucas-balancing sequences
Original research paper. Pages 390–403
Manasi K. Sahukar and Hussain Basha
Full paper (PDF, 251 Kb) | Abstract
In this paper, we define the notion of almost repdigit as a positive integer whose digits are all equal except for at most one digit, and we search all terms of the balancing and Lucas-balancing sequences which are almost repdigits. In particular, the only almost repdigits in balancing sequence are 0, 1, 6, and the only almost repdigits in Lucas-balancing sequence are 1, 3, 17, 99, 577, 3363.
A note on newly introduced arithmetic functions φ+ and σ+
Original research paper. Pages 404–409
Sagar Mandal
Full paper (PDF, 235 Kb) | Abstract
In a recent paper [7], the authors introduced new arithmetic functions
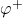
,
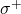
related to the classical functions
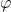
, and
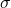
, respectively. In this note, we study the behavior of
![Rendered by QuickLaTeX.com \[\sum_{\substack{n\leq x\\ \omega(n)=2}}(\varphi^{+}-\varphi)(n),~~~\text{and}~~\sum_{\substack{n\leq x\\ \omega(n)=2}}(\sigma^{+}-\sigma)(n),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-e74e501cbc873c73673d1d7cad8f5ac0_l3.png)
for any real number 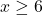 .
.
Extending the plane trigonometric proof of Fermat’s Last Theorem to the case n = 3
Original research paper. Pages 410–428
Giri Prabhakar
Full paper (PDF, 1756 Kb) | Abstract
We extend the plane trigonometric approach that we used to prove the case
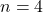
of Fermat’s Last Theorem, to the case
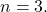
We show that all real positive triplets satisfying
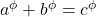
for
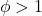
are triangles. As in the case of
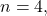
we equate the Pythagorean and Fermat descriptions of the triangles for a particular smaller side while fixing the other sides, with
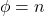
being any positive integer. We hence show the existence of Ferma
t–Pythagoras polynomials for
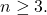
For the case
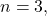
we explicitly derive an analytic expression for the roots of the polynomials. We prove from this expression that the real roots, which are equal to the length of the sides, are irrational.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP6/12/02.12.2024. Bulgarian National Science Fund bears no liability for the content of the published materials.
Volume 31 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]()
![]()
![]() with initial conditions
with initial conditions![]()
![]() in positive integers
in positive integers ![]() such that
such that ![]() and show that it has only trivial solution, namely
and show that it has only trivial solution, namely ![]()
![]()
![]() and
and![]()
![]() , where
, where ![]() are arbitrary numbers.
are arbitrary numbers.![]() and
and ![]() are given.
are given.![Rendered by QuickLaTeX.com \[\sum_{\substack{n\leq x\\ \omega(n)=2}}(\varphi^{+}-\varphi)(n),~~~\text{and}~~\sum_{\substack{n\leq x\\ \omega(n)=2}}(\sigma^{+}-\sigma)(n),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-e74e501cbc873c73673d1d7cad8f5ac0_l3.png)
![]() .
.

