Volume 31 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Editorial: A note on Papal Mathematics
Editorial. Pages 429–432
Anthony G. Shannon
Editorial (PDF, 393 Kb) | Abstract
Many recent media claims that Pope Leo XIV, Robert F. Prevost, born in the USA and elected in 2025 in succession to Pope Francis, is the first mathematician to become the Pope of the Catholic Church are questionable. That honour probably belongs to Pope Sylvester II (999–1003), Gerbert d’Aurillac, a Frenchman, educated in Moorish Spain which was then relatively advanced in mathematics and philosophy.
Fermatian row and column sums as a family of generalized integers
Original research paper. Pages 433–442
Anthony G. Shannon, Mine Uysal and Engin Özkan
Download paper (PDF, 1036 Kb) | Abstract
In this paper, we introduce some feature of the Fermatian numbers. The finite sum formulas of these numbers is calculate. The exponential generating function of Fermatian numbers is found and some of its identities is calculated. Another number sequence is obtained from the partial row sums of these numbers and these numbers were examined. At the same time, another polynomial has been defined as a generalization of these numbers, depending on powers of z.
A new symmetric weighing matrix SW(22,16)
Original research paper. Pages 443–447
Sheet Nihal Topno and Shyam Saurabh
Download paper (PDF, 180 Kb) | Abstract
The existence of symmetric weighing matrix

is settled in this note through a theorem and exhaustive search.
On sums of k-generalized Fibonacci and k-generalized Lucas numbers as first and second kinds of Thabit numbers
Original research paper. Pages 448–459
Hunar Sherzad Taher and Saroj Kumar Dash
Download paper (PDF, 307 Kb) | Abstract
Let
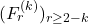
and
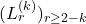
be generalizations of the Fibonacci and Lucas sequences, where
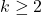
. For these sequences the initial

terms are

and

, and each subsequent term is the sum of the preceding

terms. In this paper, we determined all first and second kinds of Thabit numbers that can be expressed as the sums of

-Fibonacci and

-Lucas numbers. We employed the theory of linear forms in logarithms of algebraic numbers and a reduction method based on the continued fraction.
Solution of an odds inversion problem
Original research paper. Pages 460–470
Robert K. Moniot
Download paper (PDF, 228 Kb) | Abstract
Consider the problem of determining the possible numbers of balls of two different colors in an urn such that if two are drawn out at random, the odds that they are different colors are a given value. We present a general solution of this problem for all odds from nil to certainty. The solution methods use relatively simple concepts from number theory such as modular inverses and the Pell equation. We find upper bounds on the number of solutions and the magnitude of solutions for those cases that have at most a finite number of solutions. We also define solution classes for cases that have an infinite number of solutions, and identify cases having a determinate number of solution classes.
Recursive sufficiency for the Collatz conjecture and computational verification
Original research paper. Pages 471–480
Mohammad Ansari
Download paper (PDF, 216 Kb) | Abstract
We define the notion of recursive sufficiency for the Collatz conjecture and we use it to present some results concerning the computational verification of the conjecture. For any integer

and any recursively sufficient set
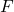
, it is proved that all integers in the interval
![Rendered by QuickLaTeX.com [1, N]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-50702b859111d0d777ecbf81b5bddffe_l3.png)
satisfy the conjecture if and only if
![Rendered by QuickLaTeX.com F\cap [1, N]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-179f48376d6318c1dc2afb44636e52b0_l3.png)
satisfies the conjecture. We offer a sequence of sieves for which the corresponding sequence of elimination percentages tends to
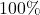
, and as a result, for any integer
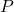
arbitrarily close to
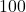
, we give a sieve whose elimination percentage is at least
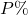
. Also, we prove that if
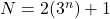
is the largest known integer for which all integers

satisfy the conjecture, then all integers
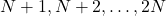
will satisfy the conjecture as well, and hence, they can be eliminated from the verification process.
The Bombieri–Vinogradov theorem for exponential sums over primes
Original research paper. Pages 481–493
Stoyan Dimitrov
Download paper (PDF, 262 Kb) | Abstract
In this paper, we revisit Lemma 18 from [2], which concerns a Bombieri–Vinogradov type theorem for exponential sums over primes. We provide a corrected version of the lemma, clarify the original arguments, and address certain inaccuracies present in the initial proof.
Gaps of size 2, 4, and (conditionally) 6 between successive odd composite numbers occur infinitely often
Original research paper. Pages 494–503
Joel E. Cohen and Dexter Senft
Download paper (PDF, 209 Kb) | Abstract
The infinite sequence of gaps (first differences) between successive odd composite numbers contains only the numbers 2, 4, and 6. We prove that, for any natural number k, the sequence of gaps contains infinitely many k-tuplets of consecutive gaps all equal to 2. Infinitely many gaps equal 4. The sequence of gaps includes infinitely many gap pairs (4, 4) if the sequence of positive primes has infinitely many pairs of successive primes that differ by 4 (cousin primes), which is unproved but holds under a conjecture of Hardy and Littlewood. Gap triplets (4, 4, 4) never occur. Infinitely many gaps equal 6 if and only if there are infinitely many twin primes. Moreover, gap pairs (6, 6) occur infinitely often if other conjectures of Hardy and Littlewood are true. Six of the 27 potential triplets of values of gaps between successive odd composite numbers never occur: (4, 4, 4), (6, 6, 6), (6, 4, 4), (4, 4, 6), (6, 2, 6), and (6, 4, 6).
On the special cases of Carmichael’s totient conjecture
Original research paper. Pages 504–534
Anthony G. Shannon, Peter J.-S. Shiue, Tian-Xiao He, and Christopher Saito
Download paper (PDF, 325 Kb) | Abstract
On an analytical study of the generalized Fibonacci polynomials
Original research paper. Pages 535–546
Leandro Rocha, Gabriel F. Pinheiro and Elen V. P. Spreafico
Download paper (PDF, 1264 Kb) | Abstract
In this work, we presented an analytical study of the generalized Fibonacci polynomial of order
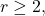
by using properties of the fundamental system associated with the generalized Fibonacci polynomial. We established the generating function and provided the asymptotic behavior for each system sequence. Moreover, the properties are extended to any generalized Fibonacci type, given the general case’s generating function and asymptotic behavior.
Binomial transform of the bivariate Fibonacci quaternion polynomials and its properties
Original research paper. Pages 547–562
Faruk Kaplan and Arzu Özkoç Öztürk
Download paper (PDF, 228 Kb) | Abstract
The primary aim of this work is to deal with binomial transforms of bivariate Fibonacci quaternion polynomial sequence. The binomial sequence of the bivariate Fibonacci quaternion polynomial is found, and then results are obtained for the recurrence relation, generating function and Binet formula. Furthermore, different types of sums are being sought for the polynomials. While working with bivariate Fibonacci quaternion polynomial sequence, we found the general formula for all sequences with quadratic recurrence relation, which includes the formulas in general terms for binomial transform. In the last part, matrix representations are derived for the corresponding binomial sequence.
Another six Fibonacci-like sequences
Original research paper. Pages 563–569
Karol Gryszka
Download paper (PDF, 182 Kb) | Abstract
We briefly describe six Fibonacci-like sequences or arbitrary order that give rise to a periodic or eventually periodic sequences. We provide some examples and demonstrate the explicit periods of these sequences.
New summation identities of hyperbolic k-Fibonacci and k-Lucas quaternions
Original research paper. Pages 570–582
A. D. Godase
Download paper (PDF, 199 Kb) | Abstract
In this paper, we introduce a set of identities involving hyperbolic

-Fibonacci quaternions and

-Lucas quaternions. Moreover, we derive summation identities for hyperbolic

-Fibonacci and

-Lucas quaternions by utilizing established properties of

-Fibonacci and

-Lucas numbers. These findings add valuable insight into the relationships between these quaternion sequences and offer valuable insights into their properties.
On a logarithmic inequality by Shenton and Kemp
Original research paper. Pages 583–587
József Sándor
Download paper (PDF, 191 Kb) | Abstract
We offer new proof and refinement of a double inequality for
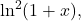
by L. R. Shenton and A. W. Kemp [11].
Affine–Hill cipher from Hadamard-type Fibonacci–Mersenne and Fibonacci-balancing p-sequences
Original research paper. Pages 588–606
Elahe Mehraban, T. Aaron Gulliver and Evren Hincal
Download paper (PDF, 229 Kb) | Abstract
In this paper, we define two new sequences using the generalized Mersenne numbers, Fibonacci

-numbers, and
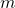
-balancing numbers. These sequences are constructed using the Hadamard-type product of their characteristic polynomials. The determinants and combinatorial and exponential representations of these new sequences are given. As an application, they are with used to generate keys for encryption for the Affine–Hill cipher using an elliptic curve and self-invertible matrix.
Graham’s number stable digits: An exact solution
Original research paper. Pages 607–616
Marco Ripà
Download paper (PDF, 1390 Kb) | Abstract
In the decimal numeral system, we prove that the well-known Graham’s number,
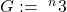
(i.e.,
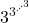
(

times)), and any base
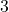
tetration whose hyperexponent is larger than

share the same
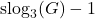
rightmost digits (where
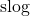
indicates the integer super-logarithm). This is an exact result since the
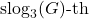
rightmost digit of

differs from the
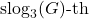
rightmost digit of
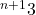
. Furthermore, we show that the
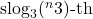
least significant digit of the difference between Graham’s number and any base
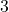
tetration whose integer hyperexponent exceeds

is
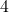
.
A note on solitary numbers
Original research paper. Pages 617–623
Sagar Mandal
Download paper (PDF, 191 Kb) | Abstract
Does 14 have a friend? Until now, this has been an open question. In this note, we prove that a potential friend
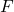
of 14 is an odd, non-square positive integer. 7 appears in the prime factorization of
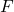
with an even exponent while at most two prime divisors of
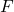
can have odd exponents in the prime factorization of
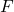
. If
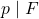
such that

is congruent to 7 modulo 8, then
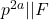
, for some positive integer

. Further, no prime divisor of
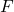
has an exponent congruent to 7 modulo 8 and no prime divisor can exceed
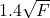
. The primes 3, 5 cannot appear simultaneously in the prime factorization of
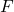
. If
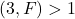
or
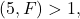
then
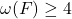
, otherwise
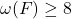
.
On circulant matrices with Fibonacci quaternions
Original research paper. Pages 624–634
Seda Yamaç Akbıyık, Fatih Yılmaz, Serhat Yıldırım, Umut Selvi
Download paper (PDF, 241 Kb) | Abstract
In literature, there exist many papers that compute determinants and some kinds of norms of circulant matrices involving some well-known number sequences. In this paper, we obtain an explicit formula for the determinant of a circulant matrix involving the well-known Fibonacci quaternions. Then, we obtain the Euclidean and spectral norms of these matrices.
Increasing sequences with decreasing prime factors
Original research paper. Pages 635–638
Noah Lebowitz-Lockard
Download paper (PDF, 180 Kb) | Abstract
We bound the length of the longest sequence of increasing numbers
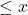
for which their smallest prime factors form a decreasing sequence. While the upper bound is unconditional, the lower bound relies on a conjecture about prime gaps.
Three versions of an inequality
Original research paper. Pages 639–645
Krassimir Atanassov
Download paper (PDF, 168 Kb) | Abstract
Three versions of the inequality
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n-1} \frac{1}{a_i(a_{i+1} + 1)} \geq \frac{n}{1 + \prod\limits_{i=1}^n a_i} - \frac{1}{a_{n}(a_1 + 1)}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-930ebb0ae69c4df242eae830fc45df2e_l3.png)
are formulated and proved, where 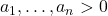 are real numbers. An open problem is formulated.
are real numbers. An open problem is formulated.
Congruences for the Apéry numbers modulo p3
Original research paper. Pages 646–657
Zhi-Hong Sun
Download paper (PDF, 262 Kb) | Abstract
On special integer linear combinations of terms of rational cycles for the generalized 3x+1 problem
Original research paper. Pages 658–666
Yagub N. Aliyev
Download paper (PDF, 264 Kb) | Abstract
In the paper, some special linear combinations of the terms of rational cycles of generalized Collatz sequences are studied. It is proved that for specific choice of the coefficients these linear combinations are integers. The discussed results are demonstrated on some examples. In some particular cases the obtained results can be used to explain some patterns of digits in p-adic representations of the terms of the rational cycles.
On a new congruence in the Catalan triangle
Original research paper. Pages 667–682
Jovan Mikić
Download paper (PDF, 246 Kb) | Abstract
For
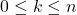
, the number
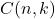
represents the number of all lattice paths in the plane from the point
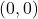
to the point
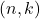
, using steps
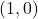
and
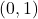
, that never rise above the main diagonal
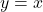
. The Fuss–Catalan number of order three
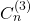
represents the number of all lattice paths in the plane from the point
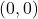
to the point
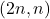
, using steps
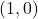
and
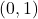
, that do not rise above the line
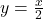
. The generalized Schröder number
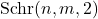
of order two represents the number of all lattice paths in the plane from the point
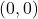
to the point
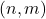
, using steps
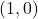
,
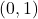
, and
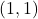
, that never go below the line
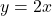
. We present a new alternating convolution formula for the numbers
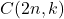
multiplied by a power of a binomial coefficient. Using a new class of binomial sums that we call
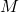
sums, we prove that this sum is divisible by
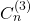
and by the central binomial coefficient
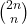
. We do this by examining the numbers
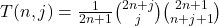
, for which we present a new combinatorial interpretation, connecting them to the generalized Schröder numbers of order two.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP6/12/02.12.2024. Bulgarian National Science Fund bears no liability for the content of the published materials.
Volume 31 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![Rendered by QuickLaTeX.com \[\udots\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-735edd36d5cd191065af2f4aba48d6b8_l3.png)
![]() Our main consideration will be the set
Our main consideration will be the set ![]() . In identifying
. In identifying ![]() for
for ![]() and
and ![]() , where
, where ![]() and
and ![]() are distinct prime numbers, we find that Carmichael’s conjecture holds for those select cases, provide an algorithm, and some related results. The conjecture remains an open problem in number theory [9].
are distinct prime numbers, we find that Carmichael’s conjecture holds for those select cases, provide an algorithm, and some related results. The conjecture remains an open problem in number theory [9].![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n-1} \frac{1}{a_i(a_{i+1} + 1)} \geq \frac{n}{1 + \prod\limits_{i=1}^n a_i} - \frac{1}{a_{n}(a_1 + 1)}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-930ebb0ae69c4df242eae830fc45df2e_l3.png)
![]() are real numbers. An open problem is formulated.
are real numbers. An open problem is formulated.![Rendered by QuickLaTeX.com \[A'_{\frac{p-1}2}\equiv \frac{p^2}{3\binom{(p-3)/2}{(p-3)/4}^2}\pmod {p^3}.\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-fdae4d8aee86359b44ad26545f0cc076_l3.png)
![]() be given by
be given by ![]()
![]() and
and ![]() We also establish the congruences for
We also establish the congruences for ![]() and
and ![]() where
where ![]() is an odd prime.
is an odd prime.![]()


