Volume 31 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Theta function identities involving fourth power
Original research paper. Pages 683–688
Praveenkumar, Siddaraju, R. Rangarajan
Download paper (PDF, 184 Kb) | Abstract
On page 241 of his Second Notebook, Ramanujan recorded one of his theta function identity, which involves the ratio of the fourth power of theta functions with respect to
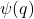
. In this article, we give a new proof for this theta function identity. Also, we give a new proof of another identity with respect to
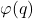
established by B. C. Berndt and we establish two new theta function identities analogous to Ramanujan’s theta function identities.
Infinite series containing quotients of central binomial coefficients
Original research paper. Pages 689–695
Zhiling Fan
Download paper (PDF, 200 Kb) | Abstract
By making use of the Wallis’ integral formulae and integration by parts, two classes of infinite series are evaluated, in closed form, in terms of
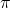
and Riemann zeta function.
On split Narayana and Narayana–Lucas hybrid quaternions
Original research paper. Pages 696–717
Pankaj Kumar and Shilpa Kapoor
Download paper (PDF, 268 Kb) | Abstract
In this paper, we introduce the novel concepts of split Narayana quaternions and split Narayana–Lucas quaternions within the innovative framework of hybrid numbers. We explore their deep connections with Narayana and Narayana–Lucas quaternions, uncovering new perspectives in this mathematical domain. Furthermore, we establish several fundamental properties, including recurrence relations, Binet formulas, generating functions, exponential generating functions, and other significant identities associated with these newly defined quaternions. Finally, to better illustrate these theoretical findings, we also provide a numerical simulation of split Narayana quaternions and split Narayana–Lucas hybrid quaternions.
On the equation 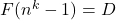
Original research paper. Pages 718–727
I. Kátai, B. M. M. Khanh, B. M. Phong
Download paper (PDF, 225 Kb) | Abstract
We prove that if
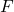
is a completely multiplicative function and
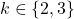
such that the equation
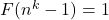
holds for every
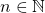
,
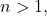
then
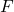
is the identity function. A similar result is proved for the equation
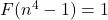
assuming a suitable conjecture concerning prime numbers. The equation
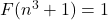
is also studied.
On some classes of binary matrices
Original research paper. Pages 728–735
Krasimir Yordzhev
Download paper (PDF, 202 Kb) | Abstract
The work considers the set
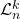
of all
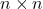
binary matrices having the same number of

units in each row and each column. The article specifically focuses on the matrices whose rows and columns are sorted lexicographically. We examine some particular cases and special properties of this matrices. Finally, we demonstrate the relationship between the Fibonacci numbers and the cardinality of two classes of
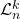
-matrices with lexicographically sorted rows and columns.
Three Diophantine equations concerning the polygonal numbers
Original research paper. Pages 736–746
Yong Zhang, Mei Jiang and Qiongzhi Tang
Download paper (PDF, 201 Kb) | Abstract
Many authors investigated the problem about the linear combination of two polygonal numbers is a perfect square, i.e., the Diophantine equation
![Rendered by QuickLaTeX.com \[mP_k(x)+nP_k(y)=z^2,\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-ea2346a3e20206a9c341d6b0cf859403_l3.png)
where 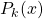 denotes the
denotes the 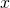 -th
-th  -polygonal number and
-polygonal number and 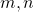 are positive integers. In this note, we continue the study of this problem in another direction and consider three Diophantine equations
are positive integers. In this note, we continue the study of this problem in another direction and consider three Diophantine equations
![Rendered by QuickLaTeX.com \[mP_k(x)-1=z^2,\quad mP_k(x)-nP_k(y)=z^2,\quad mP_k(x)-nP_k(y)=1.\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a5b8cc6be99fc9c396f48434d6acef24_l3.png)
By the theory of Pell equation and congruence, we obtain some conditions such that the above three Diophantine equations have infinitely many positive integer solutions.
(G,F)-points on ℚ-algebraic varieties
Original research paper. Pages 747–760
Yangcheng Li and Hongjian Li
Download paper (PDF, 223 Kb) | Abstract
Let
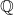
be the field of rational numbers, and let
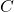
be an algebraically closed field containing
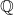
. Let
![Rendered by QuickLaTeX.com G\in \mathbb{Q}[x,y,z]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-f40fe73e09ea009b34050f7b25d73098_l3.png)
be a polynomial, then the zero set of

is
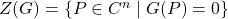
. A set

is called a
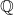
-algebraic variety if
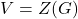
for some polynomial

in
![Rendered by QuickLaTeX.com \mathbb{Q}[x,y,z]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-dd5771523154ceaa719b4936c80a521c_l3.png)
. The set
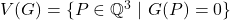
is called the set of
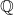
-rational points of
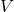
. Let
![Rendered by QuickLaTeX.com \[\begin{split} F:\quad &\mathbb{Q}^3\rightarrow \mathbb{Q}^3,\\ &(x,y,z)\mapsto (f(x),f(y),f(z)) \end{split}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-9d347a7203b02a3fd4a81a43b6fe3e72_l3.png)
be a vector function, where ![Rendered by QuickLaTeX.com f\in \mathbb{Q}[x]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-9b190e3db95644e2dccd803f6b46ab4b_l3.png) . It is easy to show that the function obtained by the composition of
. It is easy to show that the function obtained by the composition of  and
and 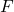 , denoted as
, denoted as 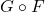 , is still in
, is still in ![Rendered by QuickLaTeX.com \mathbb{Q}[x,y,z]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-dd5771523154ceaa719b4936c80a521c_l3.png) . Moreover, let
. Moreover, let 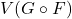 be the set of
be the set of  -rational points of the
-rational points of the  -algebraic variety corresponding to
-algebraic variety corresponding to 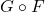 , i.e.,
, i.e., 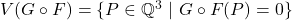 . A rational point
. A rational point 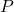 is called a
is called a 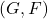 -point on
-point on 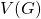 if
if 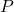 belongs to the intersection of
belongs to the intersection of 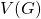 and
and 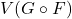 , that is
, that is 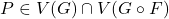 . Denote
. Denote 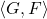 as the set consisting of all
as the set consisting of all 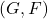 -points on
-points on 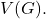 Obviously,
Obviously, 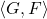 is the set of
is the set of  -rational points of a
-rational points of a  -algebraic variety, that is,
-algebraic variety, that is, 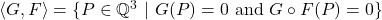 . In this paper, we consider the algebraic variety
. In this paper, we consider the algebraic variety 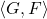 for some specific functions
for some specific functions  and
and 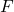 . For these specific functions
. For these specific functions  and
and 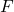 , we prove that
, we prove that 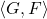 will be isomorphic to a certain elliptic curve. We also analyze some properties of these elliptic curves.
will be isomorphic to a certain elliptic curve. We also analyze some properties of these elliptic curves.
Relationship between alternating sums of powers of integers and sums of powers of integers
Original research paper. Pages 761–767
Minoru Yamamoto
Download paper (PDF, 188 Kb) | Abstract
In this note, we consider the alternating sums of powers of integers. We write alternating sum of powers of integers as the linear combination of sums of powers of integers. As the coefficients, the special value of the Euler polynomial appears.
On ψ-amicable numbers and their generalizations
Original research paper. Pages 768–775
Stoyan Dimitrov
Download paper (PDF, 197 Kb) | Abstract
In this article, we study the properties of ψ-amicable numbers. We prove that their asymptotic density relative to the positive integers is zero. We also propose generalizations of ψ-amicable numbers.
Proofs of some geometric conjectures on the power sum congruence modulo a prime
Original research paper. Pages 776–784
Pentti Haukkanen
Download paper (PDF, 257 Kb) | Abstract
A note on normal ordering of degenerate integral powers of number operator
Original research paper. Pages 785–791
Taekyun Kim, Dae San Kim and Kyo-Shin Hwang
Download paper (PDF, 140 Kb) | Abstract
This study derives the normal ordering expansion of degenerate integral powers of the number operator,
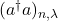
, using recurrence relations for the coefficients and an operator action on number states. Here
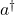
and

are respectively the boson creation and annihilation operators. We also determine the inverse of this normal ordering expansion. By analyzing diagonal coherent state elements of the degenerate integral powers of the number operator, we establish a combinatorial identity which yields a Dobinski-like formula for the degenerate Bell numbers at a specific value, connecting degenerate quantum operator calculus with combinatorics.
Cryptography using Fibonacci–Mersenne and Fibonacci-balancing p-sequences with a self-invertible matrix and the Affine–Hill cipher
Original research paper. Pages 792–818
Elahe Mehraban, T. Aaron Gulliver, Ömür Deveci and Evren Hincal
Download paper (PDF, 313 Kb) | Abstract
In this paper, we define two new sequences using the Fibonacci

-numbers, the generalized Mersenne numbers, and
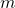
-balancing numbers. These sequences are obtained from the corresponding characteristic polynomials. The determinants and combinatorial and exponential representations of these new sequences are given. As an application, we provide two algorithms using these new sequences with self-invertible matrices and the Affine–Hill cipher.
On b-repdigit polygonal numbers
Original research paper. Pages 819–828
Adriana Mora and Eric Bravo
Download paper (PDF, 224 Kb) | Abstract
We prove a finiteness theorem concerning repdigits in base
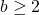
represented by a fixed quadratic polynomial. We also show that there is a finite number of polygonal numbers that are also
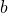
-repdigits for all
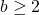
provided that
![Rendered by QuickLaTeX.com (b,s)\notin \left\{\left(\frac{8(s-2)}{(s-4)^{2}}d+1,s\right):s\in [3,13]-\{4\}\right\}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a22fb06036d4e5c5804cb081b6a59f53_l3.png)
, where
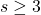
denotes the number of sides of the polygon and
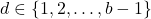
. We illustrate this result by finding all triangular, pentagonal and heptagonal numbers that are also
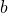
-repdigits for
![Rendered by QuickLaTeX.com b\in [2,9]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-98b8e5c1e300ead602d18ac4a2b6069d_l3.png)
. This paper is motivated by a previous work of Kafle, Luca, and Togbé who considered the same finiteness problem for
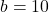
to find all pentagonal and heptagonal numbers that are also repdigits.
Alternating generalized Fibonacci sequences
Original research paper. Pages 829–838
Carlos M. da Fonseca and Paulo Saraiva
Download paper (PDF, 200 Kb) | Abstract
In a recent paper, K. T. Atanassov and A. G. Shannon introduced a Fibonacci-like sequence derived from the generalized Fibonacci sequence by incorporating alternating signs into the recurrence relation. They also proposed explicit formulas for this sequence. In this work, we present the generating function for the sequence using a matrix-based approach. Furthermore, we explore additional variations of the original definition.
Inequalities between some arithmetic functions, II
Original research paper. Pages 839–845
Krassimir Atanassov, József Sándor and Mladen Vassilev-Missana
Download paper (PDF, 212 Kb) | Abstract
As a continuation of Part I (see [1]), we offer new inequalities for classical arithmetic functions such as the Euler’s totient function, the Dedekind’s psi function, the sum of the positive divisors function, the number of divisors function, extended Jordan’s totient function, generalized Dedekind’s psi function.
On an infinite family of unipotent Sylvester–Kac-like matrices
Original research paper. Pages 846–850
Zhibin Du and Carlos M. da Fonseca
Download paper (PDF, 156 Kb) | Abstract
Classical Sylvester–Kac matrices are tridiagonal integral matrices with positive off-diagonal entries and fully integral spectra. Here, by relaxing the positivity requirement and using a lower Pascal triangle framework, we define, for each positive integer

, a unipotent Sylvester–Kac-like matrix in which

is the only eigenvalue. This construction highlights the connection to the original Sylvester–Kac matrices while introducing a new family of unipotent matrices with distinctive properties.
Power series expansions of arbitrary order functional difference equations
Original research paper. Pages 851–858
Anthony G. Shannon, Ömür Deveci and Özgür Erdağ
Download paper (PDF, 387 Kb) | Abstract
This paper looks at some real and complex generalizations of power series associated with some arbitrary order functional difference equations considered as generalizations and extensions of Fibonacci and Lucas numbers. It does this by drawing on, and interconnecting, some classic number theoretic results of Carlitz, Fasenmyer and Horadam.
Research on splitting quaternions with generalized Tribonacci hybrid number components
Original research paper. Pages 859–874
Yanni Yang and Yong Deng
Download paper (PDF, 250 Kb) | Abstract
This paper introduces the Generalized Tribonacci Hybrid Split Quaternion (GTHSQ), a novel split quaternion with coefficients derived from generalized Tribonacci hybrid numbers. This form unifies various existing number types, such as generalized hybrid Tribonacci numbers and Tribonacci numbers, offering a fresh perspective on quaternion theory. To systematically characterize GTHSQ, we develop a comprehensive mathematical framework. This includes defining GTHSQ through related number expressions, specifying its operational rules, and proving that it retains the third-order linear recurrence relation of generalized Tribonacci sequences. We derive its Binet-type formula and generating functions while exploring its core properties. Additionally, we extend classic combinatorial identities (Vajda, Catalan, Cassini) to GTHSQ, define the GTHSQ matrix, and analyze its product with the S-matrix—a generalized third-order linear recurrence sequence representation matrix—to obtain matrix and determinant expressions for GTHSQ. These findings verify the closed-form solution of GTHSQ in terms of combinatorial identities and matrix representation. Furthermore, we discuss potential applications of GTHSQ, including advancements in quaternion algebra, support for encryption algorithms in cryptography, and simplification of spatial transformations in physics, thereby providing new tools and insights for future research in quaternion theory and interdisciplinary studies.
Coefficients of symmetric power L-functions on integers under digital constraints
Original research paper. Pages 875–883
Khadija Mbarki
Download paper (PDF, 240 Kb) | Abstract
Let
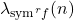
be the

-th coefficient in the Dirichlet series representing the symmetric power
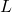
-function attached to a primitive form
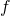
of weight

and level
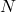
. In this paper, we give asymptotic formulas for the arithmetic mean of
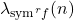
on integers under digital constraints related to the sum of digits function. Our results throw the light on the behavior of the classical function
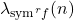
on integers in arithmetic progression related to the sum of digits function.
On q-generalized hyperharmonic numbers with two parameters
Original research paper. Pages 884–898
Neşe Ömür, Sibel Koparal and Ömer Duran
Download paper (PDF, 728 Kb) | Abstract
In this paper, we introduce
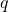
-generalized harmonic numbers with two parameters
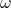
and
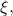
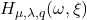
for integers
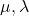
such that
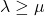
. With the help of these numbers, we define a new family of numbers which is called
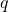
-generalized hyperharmonic numbers with two parameters
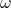
and
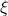
of order

,
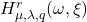
for integer

. Then, we consider special matrices whose entries are given by these numbers and give some matrix multiplications. Additionally, we derive some combinatorial identities for
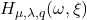
and
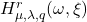
by matrix methods.
Divisibility and sequence properties of σ+ and φ+
Original research paper. Pages 899–907
Sagar Mandal
Download paper (PDF, 210 Kb) | Abstract
Inspired by Lehmer’s and Deaconescu’s conjectures, as well as various analogue problems concerning Euler’s totient function
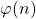
, Schemmel’s totient function
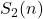
, Jordan totient function
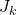
, and the unitary totient function
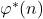
, we investigate analogous divisibility problems involving the functions
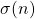
,
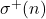
, and
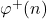
. Further, we establish some interesting properties of the sequences
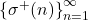
and
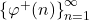
, in particular, we prove that each of these sequences contains infinitely many arithmetic progressions of length
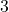
.
On the sum of partition norms and its connection to norms of partitions with parts greater than one
Original research paper. Pages 908–915
Meenakshi Rana, Harman Kaur and Abhimanyu Kumar
Download paper (PDF, 246 Kb) | Abstract
We study the
partition norm—the product of the parts of a partition—with emphasis on partitions whose parts all exceed 1. We obtain two bivariate recurrences for the sum of norms over partitions into distinct parts, including a refinement that separates the contributions of the part 1 and of the prime 2. To count partitions of

with parts greater than 1 having norm
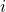
, we introduce the
restricted norm-counting function 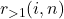
, give its two-parameter generating function, and derive recurrences and other relations. Finally, we formulate analogues of Goldbach’s and twin-prime conjectures in the language of partition norms.
Divisors and square-free divisors involving the floor function
Original research paper. Pages 916–923
B. Feng and J. Wu
Download paper (PDF, 224 Kb) | Abstract
Let
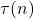
(respectively,
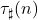
) be the number of divisors (respectively, square free divisors) of natural number

, and let
![Rendered by QuickLaTeX.com [t]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-bc8925955e6a7fe116540216f63105bd_l3.png)
be the integral part of real number
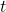
.
In this short note, we prove that for any
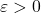
the asymptotic formula
![Rendered by QuickLaTeX.com \[\sum_{n\le x^{1/c}} g\Big(\Big[\frac{x}{n^c}\Big]\Big) = \Xi_{g, c} x^{1/c} + O_{\varepsilon}(x^{\theta_c^{\rm FW}+\varepsilon})\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-9b580b12b381a044eb880d1052a3f128_l3.png)
holds for 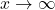 , where
, where 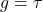 or
or 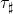 and
and
![Rendered by QuickLaTeX.com \[\Xi_{g, c} := \sum_{d=1}^{\infty} g(d)\bigg(\frac{1}{d^{1/c}} - \frac{1}{(d+1)^{1/c}}\bigg), \quad \theta_c^{\rm FW} := \begin{cases} \frac{2}{3c+2}, & \text{if $0<c\le \frac{2}{5}$}, \\\noalign{\vskip 1mm} \frac{5}{5c+6}, & \text{if $c\ge \frac{2}{5}$}\cdot \end{cases}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-37c3e2b92921e5ebc315d102533f61c4_l3.png)
This improves and generalises the corresponding results of Feng–Wu for 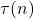 and of Zhang for
and of Zhang for 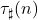 with
with 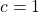 , respectively.
, respectively.
Transformations of Pythagorean triples generated by generalized Fibonacci numbers
Original research paper. Pages 924–928
Jathan Austin
Download paper (PDF, 189 Kb) | Abstract
We present matrices that transform Pythagorean triples arising from generalized Fibonacci sequences into other such triples. We also show that entries in the powers of such matrices can be expressed in terms of generalized Fibonacci sequences.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP6/12/02.12.2024. Bulgarian National Science Fund bears no liability for the content of the published materials.
Volume 31 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]()
![]()
![]() denotes the
denotes the ![]() -th
-th ![]() -polygonal number and
-polygonal number and ![]() are positive integers. In this note, we continue the study of this problem in another direction and consider three Diophantine equations
are positive integers. In this note, we continue the study of this problem in another direction and consider three Diophantine equations ![]()
![]()
![]() . It is easy to show that the function obtained by the composition of
. It is easy to show that the function obtained by the composition of ![]() and
and ![]() , denoted as
, denoted as ![]() , is still in
, is still in ![]() . Moreover, let
. Moreover, let ![]() be the set of
be the set of ![]() -rational points of the
-rational points of the ![]() -algebraic variety corresponding to
-algebraic variety corresponding to ![]() , i.e.,
, i.e., ![]() . A rational point
. A rational point ![]() is called a
is called a ![]() -point on
-point on ![]() if
if ![]() belongs to the intersection of
belongs to the intersection of ![]() and
and ![]() , that is
, that is ![]() . Denote
. Denote ![]() as the set consisting of all
as the set consisting of all ![]() -points on
-points on ![]() Obviously,
Obviously, ![]() is the set of
is the set of ![]() -rational points of a
-rational points of a ![]() -algebraic variety, that is,
-algebraic variety, that is, ![]() . In this paper, we consider the algebraic variety
. In this paper, we consider the algebraic variety ![]() for some specific functions
for some specific functions ![]() and
and ![]() . For these specific functions
. For these specific functions ![]() and
and ![]() , we prove that
, we prove that ![]() will be isomorphic to a certain elliptic curve. We also analyze some properties of these elliptic curves.
will be isomorphic to a certain elliptic curve. We also analyze some properties of these elliptic curves.![]()
![]() is a prime. For
is a prime. For ![]() , the nontrivial solutions lie on the “lines”
, the nontrivial solutions lie on the “lines” ![]() where
where ![]() ranges over the
ranges over the ![]() -th roots of
-th roots of ![]() modulo
modulo ![]() . The total number of solutions is
. The total number of solutions is ![]() if
if ![]() divides
divides ![]() , and
, and ![]() otherwise, where
otherwise, where ![]() . For each
. For each ![]() , the lines are equally spaced.
, the lines are equally spaced.![]()
![]() , where
, where ![]() or
or ![]() and
and![Rendered by QuickLaTeX.com \[\Xi_{g, c} := \sum_{d=1}^{\infty} g(d)\bigg(\frac{1}{d^{1/c}} - \frac{1}{(d+1)^{1/c}}\bigg), \quad \theta_c^{\rm FW} := \begin{cases} \frac{2}{3c+2}, & \text{if $0<c\le \frac{2}{5}$}, \\\noalign{\vskip 1mm} \frac{5}{5c+6}, & \text{if $c\ge \frac{2}{5}$}\cdot \end{cases}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-37c3e2b92921e5ebc315d102533f61c4_l3.png)
![]() and of Zhang for
and of Zhang for ![]() with
with ![]() , respectively.
, respectively.

