Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On the bivariate Padovan polynomials matrix
Original research paper. Pages 407–420
Orhan Dişkaya, Hamza Menken and Paula Maria Machado Cruz Catarino
Full paper (PDF, 237 Kb) | Abstract
In this paper, we intruduce the bivariate Padovan sequence we examine its various identities. We define the bivariate Padovan polynomials matrix. Then, we find the Binet formula, generating function and exponential generating function of the bivariate Padovan polynomials matrix. Also, we obtain a sum formula and its series representation.
A note on a generalization of Riordan’s combinatorial identity via a hypergeometric series approach
Original research paper. Pages 421–425
Dongkyu Lim
Full paper (PDF, 164 Kb) | Abstract
In this note, an attempt has been made to generalize the well-known and useful Riordan’s combinatorial identity via a hypergeometric series approach.
On vertex resolvability of a circular ladder of nonagons
Original research paper. Pages 426–444
Sunny Kumar Sharma and Vijay Kumar Bhat
Full paper (PDF, 288 Kb) | Abstract
Let
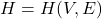
be a non-trivial simple connected graph with edge and vertex set
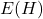
and
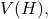
respectively. A subset
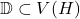
with distinct vertices is said to be a vertex resolving set in
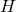
if for each pair of distinct vertices

and
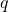
in
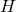
we have
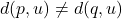
for some vertex
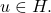
A resolving set
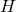
with minimum possible vertices is said to be a metric basis for
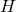
. The cardinality of metric basis is called the metric dimension of
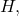
denoted by
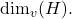
In this paper, we prove that the metric dimension is constant and equal to
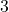
for certain closely related families of convex polytopes.
The mean value of the function 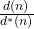 in arithmetic progressions
in arithmetic progressions
Original research paper. Pages 445–453
Ouarda Bouakkaz and Abdallah Derbal
Full paper (PDF, 304 Kb) | Abstract
Let
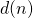
and
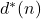
be, respectively, the number of divisors and the number of unitary divisors of an integer
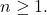
A divisor
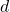
of an integer is to be said unitary if it is prime over
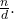
In this paper, we study the mean value of the function
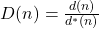
in the arithmetic progressions
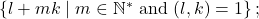
this leads back to the study of the real function
![Rendered by QuickLaTeX.com x\mapsto S(x;k,l)=\underset{n\equiv l[k]}{\sum\limits_{ n \leq x}} D(n).](https://nntdm.net/wp-content/ql-cache/quicklatex.com-f49276ea09f24f9f4ca13b6046a65abc_l3.png)
We prove that
![Rendered by QuickLaTeX.com \[S(x;k,l)=A(k)x +\mathcal{O}_{k}\left(x\exp \left( -\frac{\theta}{2}\sqrt{(2\ln x)(\ln\ln x)}\right) \right) \left( 0<\theta<1 \right),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-242123258b3de18b0a221041eac07e84_l3.png)
where 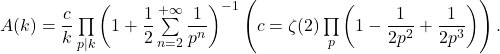
On certain inequalities for the prime counting function – Part III
Original research paper. Pages 454–461
József Sándor
Full paper (PDF, 259 Kb) | Abstract
As a continuation of [10] and [11], we offer some new inequalities for the prime counting function
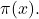
Particularly, a multiplicative analogue of the Hardy–Littlewood conjecture is provided. Improvements of the converse of Landau’s inequality are given. Some results on
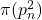
are offered,
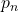
denoting the

-th prime number. Results on
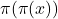
are also considered.
Narayana sequence and the Brocard–Ramanujan equation
Original research paper. Pages 462–473
Mustafa Ismail, Salah Eddine Rihane and M. Anwar
Full paper (PDF, 202 Kb) | Abstract
Let
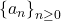
be the Narayana sequence defined by the recurrence
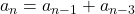
for all
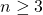
with intital values
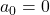
and
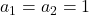
. In this paper, we fully characterize the
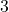
-adic valuation of
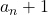
and
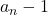
and then we find all positive integer solutions
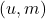
to the Brocard–Ramanujan equation
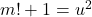
where
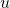
is a Narayana number.
Digits of powers of 2 in ternary numeral system
Original research paper. Pages 474–485
Yagub N. Aliyev
Full paper (PDF, 790 Kb) | Abstract
We study the digits of the powers of 2 in the ternary number system. We propose an algorithm for doubling numbers in ternary numeral system. Using this algorithm, we explain the appearance of “stairs” formed by 0s and 2s when the numbers
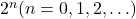
are written vertically so that for example the last digits are forming one column, the second last digits are forming another column, and so forth. We use the patterns formed by the leftmost digits, and the patterns formed by the rightmost digits to prove that the sizes of these blocks of 0s and 2s are unbounded. We also study how this regularity changes when the digits are taken between the left end and the right end of the numbers.
Explicit relations on the degenerate type 2-unified Apostol–Bernoulli, Euler and Genocchi polynomials and numbers
Original research paper. Pages 486–494
Burak Kurt
Full paper (PDF, 207 Kb) | Abstract
The main aim of this paper is to introduce and investigate the degenerate type 2-unified Apostol–Bernoulli, Euler and Genocchi polynomials by using monomiality principle and operational methods. We give explicit relations and some identities for the degenerate type 2-unified Apostol–Bernoulli, Euler and Genocchi polynomials.
Solution to a pair of linear, two-variable, Diophantine equations with coprime coefficients from balancing and Lucas-balancing numbers
Original research paper. Pages 495–502
R. K. Davala
Full paper (PDF, 222 Kb) | Abstract
Let
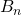
and
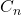
be the

-th balancing and Lucas-balancing numbers, respectively. We consider the Diophantine equations
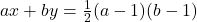
and
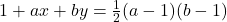
for
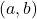
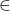
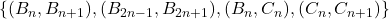
and present the non-negative integer solutions of the Diophantine equations in each case.
Coding theory on the generalized balancing sequence
Original research paper. Pages 503–524
Elahe Mehraban and Mansour Hashemi
Full paper (PDF, 278 Kb) | Abstract
In this paper, we introduce the generalized balancing sequence and its matrix. Then by using the generalized balancing matrix, we give a coding and decoding method.
Enumeration of cyclic vertices and components over the congruence 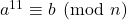
Original research paper. Pages 525–537
Sanjay Kumar Thakur, Pinkimani Goswami and Gautam Chandra Ray
Full paper (PDF, 3.6 Mb) | Abstract
For each positive integer

, we assign a digraph
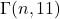
whose set of vertices is
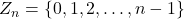
and there exists exactly one directed edge from the vertex

to the vertex
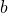
iff
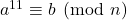
. Using the ideas of modular arithmetic, cyclic vertices are presented and established for
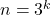
in the digraph
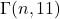
. Also, the number of cycles and the number of components in the digraph
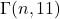
is presented for
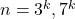
with the help of Carmichael’s lambda function. It is proved that for
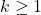
, the number of components in the digraph
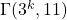
is
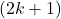
and for
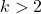
the digraph
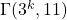
has
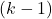
non-isomorphic cycles of length greater than
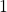
, whereas the number of components of the digraph
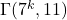
is
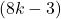
.
The 2-successive partial Bell polynomials
Original research paper. Pages 538–544
Meriem Tiachachat and Miloud Mihoubi
Full paper (PDF, 203 Kb) | Abstract
In this paper, we discuss a new class of partial Bell polynomials. The first section gives an overview of partial Bell polynomials and their related 2-successive Stirling numbers. In the second section, we introduce the concept of 2-successive partial Bell polynomials. We give an explicit formula for computing these polynomials and establish their generating function. In addition, we derive several recurrence relations that govern the behaviour of these polynomials. Furthermore, we study specific cases to illustrate the applicability and versatility of this new class of polynomials.
On ternary Dejean words avoiding 010
Original research paper. Pages 545–548
Pascal Ochem
Full paper (PDF, 187 Kb) | Abstract
Thue has shown the existence of three types of infinite square-free words over
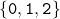
avoiding the factor
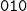
. They respectively avoid
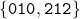
,
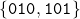
, and
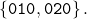
Also Dejean constructed an infinite
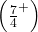
-free ternary word. A word is
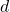
-directed if it does not contain both a factor of length
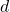
and its mirror image. We show that there exist exponentially many
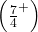
-free
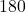
-directed ternary words avoiding
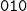
. Moreover, there does not exist an infinite
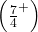
-free
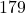
-directed ternary word avoiding
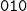
.
The Dirichlet divisor problem over square-free integers and unitary convolutions
Original research paper. Pages 549–556
André Pierro de Camargo
Full paper (PDF, 242 Kb) | Abstract
We obtain an asymptotic formula for the sum
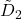
of the divisors of all square-free integers less than or equal to
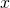
, with error term
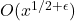
. This improves the error term
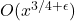
presented in [7] obtained via analytical methods. Our approach is elementary and it is based on the connections between the function
and unitary convolutions.
On a sequence derived from the Laplace transform of the characteristic polynomial of the Fibonacci sequence
Original research paper. Pages 557–563
Carlos M. da Fonseca and Anthony G. Shannon
Full paper (PDF, 350 Kb) | Abstract
Recently, based on the Laplace transform of the characteristic polynomial of the Fibonacci sequence, Deveci and Shannon established a new sequence and analysed some of its properties. They disclosed in particular the odd terms. In this short note, we provide a matricial representation for this sequence as well as one in terms of the Chebyshev polynomials of the second kind. The subsequence of the even terms is also disclosed.
The average value of a certain number-theoretic function over the primes
Original research paper. Pages 564–570
Louis Rubin
Full paper (PDF, 212 Kb) | Abstract
We consider functions
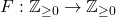
for which there exists a positive integer

such that two conditions hold:
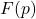
divides

for every prime

, and for each divisor
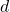
of

and every prime

, we have that
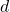
divides
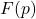
iff
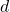
divides
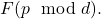
Following an approach of Khrennikov and Nilsson, we employ the prime number theorem for arithmetic progressions to derive an expression for the average value of such an
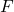
over all primes
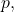
recovering a theorem of these authors as a special case. As an application, we compute the average number of

-periodic points of a multivariate power map defined on a product
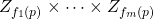
of cyclic groups, where
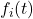
is a polynomial.
On properties of generalized Tridovan numbers
Original research paper. Pages 571–588
Yüksel Soykan, Nejla Özmen and Inci Okumuş
Full paper (PDF, 240 Kb) | Abstract
In this paper, we examine generalized Tridovan sequences and treat in detail two cases called Tridovan sequences and Tridovan–Lucas sequences. We present Binet’s formulas, generating functions, Simson formulas, and the summation formulas for these sequences. In addition, we give some identities and matrices related to these sequences.
Objects generated by an arbitrary natural number. Part 4: New aspects
Original research paper. Pages 589–597
Krassimir Atanassov
Full paper (PDF, 229 Kb) | Abstract
The set
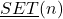
, generated by an arbitrary natural number

, was defined in [3]. There, and in [5,6], some arithmetic functions and arithmetic operators of a modal and topological types are defined over the elements of
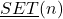
. Here, over the elements of
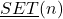
new arithmetic functions are defined and some of their basic properties are studied. Two standard modal topological structures over
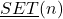
are described. Perspectives for future research are discussed.
On special exponential Diophantine equations
Original research paper. Pages 598–602
Tomáš Riemel
Full paper (PDF, 165 Kb) | Abstract
In this paper, we will focus on the study of a special type of exponential Diophantine equations, including a proof. The main contribution of this article is the mentioned type of equations, which can only be solved by the methods of elementary mathematics.
The group determinants for ℤn × H
Original research paper. Pages 603–619
Bishnu Paudel and Chris Pinner
Full paper (PDF, 293 Kb) | Abstract
Let
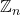
denote the cyclic group of order

. We show how the group determinant for
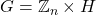
can be simply written in terms of the group determinant for
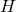
. We use this to get a complete description of the integer group determinants for
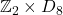
where
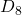
is the dihedral group of order
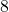
, and
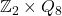
where
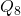
is the quaternion group of order
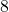
.
Topological structures induced by chromatic partitioning of vertex set of graphs
Original research paper. Pages 620–634
K. Lalithambigai and P. Gnanachandra
Full paper (PDF, 207 Kb) | Abstract
This paper presents a method of constructing topologies on vertex set of a graph

induced by chromatic partition of vertex set of the graph. It introduces colour lower approximation and colour upper approximation of vertex induced subgraphs and acquaints the open and closed sets of the topology generated by chromatic partition on the vertex set of graphs. It explores some of the properties of colour lower approximation and colour upper approximation of vertex induced subgraphs. It also establishes some new subgraphs based on the colour lower approximation and colour upper approximation and some of their properties have been studied.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP4/30/2022.
Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() in arithmetic progressions
in arithmetic progressions![Rendered by QuickLaTeX.com x\mapsto S(x;k,l)=\underset{n\equiv l[k]}{\sum\limits_{ n \leq x}} D(n).](https://nntdm.net/wp-content/ql-cache/quicklatex.com-f49276ea09f24f9f4ca13b6046a65abc_l3.png) We prove that
We prove that
![]()
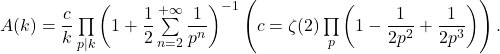
![]()


