Ouarda Bouakkaz and Abdallah Derbal
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 3, Pages 445–453
DOI: 10.7546/nntdm.2023.29.3.445-453
Full paper (PDF, 304 Kb)
Details
Authors and affiliations
Ouarda Bouakkaz ![]()
Laboratoire d’Equations aux Derivées Partielles Non linéaires et Histoire des Mathématiques,
Ecole Normale Supérieure, Vieux-Kouba Alger, Algérie
Abdallah Derbal ![]()
![]()
Laboratoire d’Equations aux Derivées Partielles Non linéaires et Histoire des Mathématiques,
Ecole Normale Supérieure, Vieux-Kouba Alger, Algérie
Abstract
Let ![]() and
and ![]() be, respectively, the number of divisors and the number of unitary divisors of an integer
be, respectively, the number of divisors and the number of unitary divisors of an integer ![]() A divisor
A divisor ![]() of an integer is to be said unitary if it is prime over
of an integer is to be said unitary if it is prime over ![]() In this paper, we study the mean value of the function
In this paper, we study the mean value of the function ![]() in the arithmetic progressions
in the arithmetic progressions ![]() this leads back to the study of the real function
this leads back to the study of the real function ![Rendered by QuickLaTeX.com x\mapsto S(x;k,l)=\underset{n\equiv l[k]}{\sum\limits_{ n \leq x}} D(n).](https://nntdm.net/wp-content/ql-cache/quicklatex.com-f49276ea09f24f9f4ca13b6046a65abc_l3.png) We prove that
We prove that
![]()
where 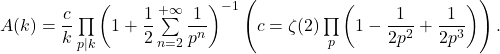
Keywords
- Divisors
- Unitary divisors of integer
- Riemann zeta function
- Dirichlet function
- Dirichlet characters modulo k
2020 Mathematics Subject Classification
- 11M32
- 11M06
- 11M38
- 11N05
- 11F68
References
- Apostol, T. M. (1976). Introduction to Analytic Number Theory. Springer-Verlag, New York, Heidelberg, Berlin.
- Balazard, M., & Tenenbaum, G. (1998). Sur la Repartition des Valeurs de la Fonction d’Euler. Composito Mathematica, 110, 239–250.
- Derbal, A. (2009). Une Forme Effective D’un Theoreme de Batemane Sur la fonction PHI D’Euler. Integers, 9, 735–744.
- Derbal, A. (2012). Ordre maximum d’une fonction liée aux diviseurs d’un nombre entier. Integers, 12, Article A44.
- Derbal, A., & Karras, M. (2016). Valeurs moyennes d’une fonction liée aux diviseurs d’un nombre entier. Comptes Rendus Mathematique, Acad. Sci. Paris, 354(6), 555–558.
- Ford, K. (2002). Vingradov’s integral and bounds for the Riemann zeta function. Proceedings of the London Mathematical Society, 85, 565–633.
- Parent, D. P. (1978). Exercices de Théorie des Nombres. Gauthier-Villars, Paris.
Manuscript history
- Received: 10 October 2022
- Revised: 13 March 2023
- Accepted: 16 June 2023
- Online First: 3 July 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Bouakkaz, O., & Derbal, A. (2023). The mean value of the function ![]() in arithmetic progressions. Notes on Number Theory and Discrete Mathematics, 29(3), 445-453, DOI: 10.7546/nntdm.2023.29.3.445-453.
in arithmetic progressions. Notes on Number Theory and Discrete Mathematics, 29(3), 445-453, DOI: 10.7546/nntdm.2023.29.3.445-453.


