Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Quotients of arithmetical functions under the Dirichlet convolution
Original research paper. Pages 185–194
Pentti Haukkanen
Full paper (PDF, 189 Kb) | Abstract
We study existence of a solution of the arithmetical equation
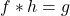
in
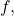
where

is the Dirichlet convolution of arithmetical functions
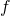
and
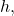
and derive an explicit expression for the solution. As applications we obtain expressions for the Möbius function
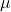
and the so-called totients. As applications we also present our results on the arithmetical equation
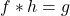
in the language of Cauchy convolution and further deconvolution in discrete linear systems.
A note on telephone numbers and their matrix generators
Original research paper. Pages 195–203
Francisco Regis Vieira Alves, Renata Passos Machado Vieira and Paula Maria Machado Cruz Catarino
Full paper (PDF, 150 Kb) | Abstract
In the present work, we indicate some matrix properties that allow us to determine new relationships involving telephone numbers and some products that allow us to obtain telephone terms, based on second-order matrices.
Some identities involving Chebyshev polynomials, Fibonacci polynomials and their derivatives
Original research paper. Pages 204–215
Jugal Kishore and Vipin Verma
Full paper (PDF, 186 Kb) | Abstract
In this paper, we will derive the explicit formulae for Chebyshev polynomials of the third and fourth kind with odd and even indices using the combinatorial method. Similar results are also deduced for their r-th derivatives. Finally, some identities involving Chebyshev polynomials of the third and fourth kind with even and odd indices and Fibonacci polynomials with negative indices are obtained.
Some new relations between T(a1,a2,a3,a4,a5; n) and N(a1,a2,a3,a4,a5; n)
Original research paper. Pages 216–225
Vandna and Mandeep Kaur
Full paper (PDF, 181 Kb) | Abstract
Let
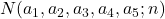
and
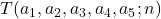
count the representations of

as
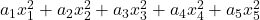
and
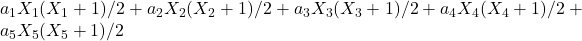
, respectively, where
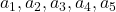
are positive integers,
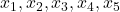
are integers and
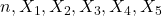
are nonnegative integers. In this paper, we establish some new relations between
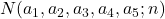
and
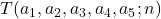
. Also, we prove that
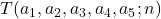
is a linear combination of
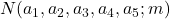
and
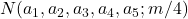
, where
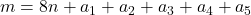
, for various values of
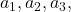
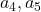
.
The quaternion-type cyclic-Fibonacci sequences in groups
Original research paper. Pages 226–240
Nazmiye Yilmaz, Esra Kırmızı Çetinalp and Ömür Deveci
Full paper (PDF, 267 Kb) | Abstract
In this paper, we define the six different quaternion-type cyclic-Fibonacci sequences and present some properties, such as, the Cassini formula and generating function. Then, we study quaternion-type cyclic-Fibonacci sequences modulo
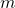
. Also we present the relationships between the lengths of periods of the quaternion-type cyclic-Fibonacci sequences of the first, second, third, fourth, fifth and sixth kinds modulo
m and the generating matrices of these sequences. Finally, we introduce the quaternion-type cyclic-Fibonacci sequences in finite groups. We calculate the lengths of periods for these sequences of the generalized quaternion groups and obtain quaternion-type cyclic-Fibonacci orbits of the quaternion groups
Q8 and
Q16 as applications of the results.
Representations of positive integers as sums of arithmetic progressions, I
Original research paper. Pages 241–259
Chungwu Ho, Tian-Xiao He and Peter J.-S. Shiue
Full paper (PDF, 267 Kb) | Abstract
This is the first part of a two-part paper. Our paper was motivated by two classical papers: A paper of Sir Charles Wheatstone published in 1844 on representing certain powers of an integer as sums of arithmetic progressions and a paper of J. J. Sylvester published in 1882 for determining the number of ways a positive integer can be represented as the sum of a sequence of consecutive integers. There have been many attempts to extend Sylvester Theorem to the number of representations for an integer as the sums of different types of sequences, including sums of certain arithmetic progressions. In this part of the paper, we will make yet one more extension: We will describe a procedure for computing the number of ways a positive integer can be represented as the sums of all possible arithmetic progressions, together with an example to illustrate how this procedure can be carried out. In the process of doing this, we will also give an extension of Wheatstone’s work. In the second part of the paper, we will continue on the problems initiated by Wheatstone by studying certain relationships among the representations for different powers of an integer as sums of arithmetic progressions.
Representations of positive integers as sums of arithmetic progressions, II
Original research paper. Pages 260–275
Chungwu Ho, Tian-Xiao He and Peter J.-S. Shiue
Full paper (PDF, 265 Kb) | Abstract
As mentioned in the first part of this paper, our paper was motivated by two classical papers on the representations of integers as sums of arithmetic progressions. One of them is a paper by Sir Charles Wheatstone and the other is a paper by James Joseph Sylvester. Part I of the paper, though contained some extensions of Wheatstone’s work, was primarily devoted to extensions of Sylvester’s Theorem. In this part of the paper, we will pay more attention on the problems initiated by of Wheatstone on the representations of powers of integers as sums of arithmetic progressions and the relationships among the representations for different powers of the integer. However, a large part in this portion of the paper will be devoted to the extension of a clever method recently introduced by S. B. Junaidu, A. Laradji, and A. Umar and the problems related to the extension. This is because that this extension, not only will be our main tool for study ing the relationships of the representations of different powers of an integer, but also seems to be interesting in its own right. In the process of doing this, we need to use a few results from the first part of the paper. On the other hand, some of our results in this part will also provide certain new information on the problems studied in the first part. However, for readers who are interested primarily in the results of this part, we have repeated some basic facts from Part I of the paper so that the reader can read this part independently from the first part.
New properties of divisors of natural number
Original research paper. Pages 276–283
Hamilton Brito da Silva
Full paper (PDF, 298 Kb) | Abstract
The divisors of a natural number are very important for several areas of mathematics, representing a promising field in number theory. This work sought to analyze new relations involving the divisors of natural numbers, extending them to prime numbers. These are relations that may have an interesting application for counting the number of divisors of any natural number and understanding the behavior of prime numbers. They are not a primality test, but they can be a possible tool for this and could also be useful for understanding the Riemann’s zeta function that is strongly linked to the distribution of prime numbers.
A class of solutions of the equation d(n2) = d(φ(n))
Original research paper. Pages 284–309
Zahra Amroune, Djamel Bellaouar and Abdelmadjid Boudaoud
Full paper (PDF, 309 Kb) | Abstract
For any positive integer

let
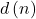
and
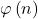
be the number of divisors of

and the Euler’s phi function of

, respectively. In this paper we present some notes on the equation
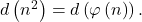
In fact, we characterize a class of solutions that have at most three distinct prime factors. Moreover, we show that Dickson’s conjecture implies that
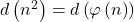
infinitely often.
Unrestricted Tribonacci and Tribonacci–Lucas quaternions
Original research paper. Pages 310–321
Gonca Kızılaslan and Leyla Karabulut
Full paper (PDF, 287 Kb) | Abstract
We define a generalization of Tribonacci and Tribonacci–Lucas quaternions with arbitrary Tribonacci numbers and Tribonacci–Lucas numbers coefficients, respectively. We get generating functions and Binet’s formulas for these quaternions. Furthermore, several sum formulas and a matrix representation are obtained.
On the k-Fibonacci and k-Lucas spinors
Original research paper. Pages 322–335
Munesh Kumari, Kalika Prasad and Robert Frontczak
Full paper (PDF, 285 Kb) | Abstract
In this paper, we introduce a new family of sequences called the k-Fibonacci and k-Lucas spinors. Starting with the Binet formulas we present their basic properties, such as Cassini’s identity, Catalan’s identity, d’Ocagne’s identity, Vajda’s identity, and Honsberger’s identity. In addition, we discuss their generating functions. Finally, we obtain sum formulae and relations between k-Fibonacci and k-Lucas spinors.
p-Analogue of biperiodic Pell and Pell–Lucas polynomials
Original research paper. Pages 336–347
Bahar Kuloğlu, Engin Özkan and Anthony G. Shannon
Full paper (PDF, 944 Kb) | Abstract
In this study, a binomial sum, unlike but analogous to the usual binomial sums, is expressed with a different definition and termed the p-integer sum. Based on this definition, p-analogue Pell and Pell–Lucas polynomials are established and the generating functions of these new polynomials are obtained. Some theorems and propositions depending on the generating functions are also expressed. Then, by association with these, the polynomials of so-called ‘incomplete’ number sequences have been obtained, and elegant summation relations provided. The paper has also been placed in the appropriate historical context for ease of further development.
On the multiplicative group generated by ![Rendered by QuickLaTeX.com \Big\{{[\sqrt {2}n]\over n}~\mid~n\in\mathbb{N} \Big\}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-69d71a993f082e99867985b1f8b06fee_l3.png) . V
. V
Original research paper. Pages 348–353
I. Kátai and B. M. Phong
Full paper (PDF, 291 Kb) | Abstract
Let
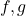
be completely multiplicative functions,
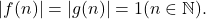
Assume that
![Rendered by QuickLaTeX.com \[{1\over {\log x}}\sum_{n\le x}{\vert g([\sqrt{2}n])-Cf(n)\vert\over n}\to 0 \quad (x\to\infty).\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-e8ea662ba97cdcb125d20fe471e79f98_l3.png)
Then
![Rendered by QuickLaTeX.com \[f(n)=g(n)=n^{i\tau},\quad C=(\sqrt{2})^{i\tau}, \tau\in \mathbb{R}.\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a2988dcf8e76b00dea69cca0b375c849_l3.png)
Intersection of Padovan and Tribonacci sequences
Original research paper. Pages 354–359
Nurretin Irmak and Abdullah Açikel
Full paper (PDF, 276 Kb) | Abstract
Assume that
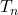
is the

-th term of Tribonacci sequence and
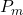
is the
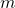
-th term of Padovan sequence. In this paper we solve the equation
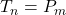
completely.
Recurrence relations connecting mock theta functions and restricted partition functions
Original research paper. Pages 360–371
M. Rana, H. Kaur and K. Garg
Full paper (PDF, 234 Kb) | Abstract
In this paper, we provide some recurrence relations connecting restricted partition functions and mock theta functions. Elementary manipulations are used including Jacobi triple product identity, Euler’s pentagonal number theorem, and Ramanujan’s theta functions for finding the recurrence relations.
A note on the length of some finite continued fractions
Original research paper. Pages 372–377
Khalil Ayadi and Chiheb Ben Bechir
Full paper (PDF, 225 Kb) | Abstract
In this paper, based on a 2008 result of Lasjaunias, we compute the lengths of simple continued fractions for some rational numbers whose numerators and denominators are explicitly given.
On certain arithmetical functions of exponents in the factorization of integers
Original research paper. Pages 378–388
József Sándor and Krassimir T. Atanassov
Full paper (PDF, 246 Kb) | Abstract
Some new results for the maximum and minimum exponents in factorizing integers are obtained. Related functions and generalized arithmetical functions are also introduced.
Hyperbolic Horadam hybrid functions
Original research paper. Pages 389–401
Efruz Özlem Mersin
Full paper (PDF, 213 Kb) | Abstract
The aim of this paper is to introduce the hybrid form of the hyperbolic Horadam function and to investigate some of its properties such as the generating function. Another aim is to define hyperbolic Horadam hybrid sine and cosine functions and their symmetrical forms. For newly defined functions, some properties such as the recursive relations, derivatives, Cassini and De Moivre type identities are examined. In addition, the quasi-sine Horadam hybrid function and three-dimensional Horadam hybrid spiral are defined.
A note on generating primitive Pythagorean triples using matrices
Original research paper. Pages 402–406
Jathan Austin
Full paper (PDF, 145 Kb) | Abstract
We present matrices that generate families of primitive Pythagorean triples that arise from generalized Fibonacci sequences. We then present similar results for generalized Lucas sequences and primitive Pythagorean triples.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP4/30/2022.
Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() . V
. V ![Rendered by QuickLaTeX.com \[{1\over {\log x}}\sum_{n\le x}{\vert g([\sqrt{2}n])-Cf(n)\vert\over n}\to 0 \quad (x\to\infty).\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-e8ea662ba97cdcb125d20fe471e79f98_l3.png)
![]()


