Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Pauli–Leonardo quaternions
Original research paper. Pages 1–16
Zehra İşbilir, Mahmut Akyiğit and Murat Tosun
Full paper (PDF, 267 Kb) | Abstract
In this study, we define Pauli–Leonardo quaternions by taking the coefficients of the Pauli quaternions as Leonardo numbers. We give the recurrence relation, Binet formula, generating function, exponential generating function, some special equalities, and the sum properties of these novel quaternions. In addition, we investigate the interrelations between Pauli–Leonardo quaternions and the Pauli–Fibonacci, Pauli–Lucas quaternions. Moreover, we create some algorithms that determine the terms of the Pauli–Leonardo quaternions. Finally, we generate the matrix representations of the Pauli–Leonardo quaternions and ℝ-linear transformations.
On distribution of the number of semisimple rings of order at most x in an arithmetic progression
Original research paper. Pages 17–23
Thorranin Thansri, Teerapat Srichan and Pinthira Tangsupphathawat
Full paper (PDF, 190 Kb) | Abstract
Let
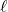
and
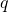
denote relatively prime positive integers. In this article, we derive the asymptotic formula for the summation
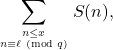
where 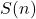 denotes the number of non-isomorphic finite semisimple rings with
denotes the number of non-isomorphic finite semisimple rings with  elements.
elements.
A note on the number an+ bn – dcn
Original research paper. Pages 24–29
Nguyen Viet Dung and Luu Ba Thang
Full paper (PDF, 216 Kb) | Abstract
We say that a positive integer
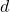
is special number of degree

if for every integer
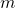
, there exist nonzero integers
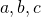
such that
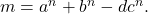
In this paper, we investigate some necessary conditions on

for existing a special number of degree
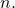
Two generalizations of Liouville λ function
Original research paper. Pages 30–39
André Pierro de Camargo
Full paper (PDF, 255 Kb) | Abstract
We study the properties of two classes of functions
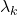
and
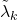
that generalize the Liouville
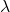
function, including some equivalencies between the Riemann hypothesis and some assertions about the asymptotic behavior of the summatory functions of
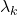
and
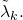
Similar results are obtained for the generalization of the Möbius function considered by Tanaka.
A study of the complexification process of the (s,t)-Perrin sequence
Original research paper. Pages 40–47
Renata Passos Machado Vieira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 181 Kb) | Abstract
The present article deals with the study of the generalized (s,t)-Perrin sequence in its complex process. Thus, from the one-dimensional model of the generalized (s,t)-Perrin sequence, imaginary units are inserted, starting with the insertion of unit i, called two-dimensional relations. Altogether, we have the n-dimensional relationships of the generalized (s,t)-Perrin sequence.
Transcendental properties of the certain mix infinite products
Original research paper. Pages 48–61
Eiji Miyanohara
Full paper (PDF, 264 Kb) | Abstract
Let
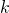
and
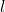
be two multiplicatively independent positive integers and
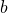
be an integer with
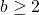
. Let
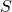
be a finite set of integers. Nishioka proved that for any algebraic number
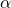
with
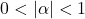
the infinite products
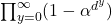
(
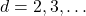
) are algebraically independent over
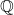
. As her result, for example, the transcendence of
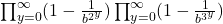
is deduced. On the other hand, Tachiya, Amou–Väänänen investigated the certain infinite products which satisfy infinite chains of Mahler functional equation. The special case of the result of Tachiya shows that the infinite product
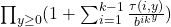
with
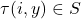
(
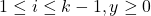
) is either rational or transcendental.
In this paper, we prove that the infinite product 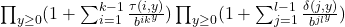 with
with 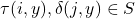
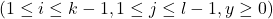 is either rational or transcendental. Moreover, we give sufficient conditions that
is either rational or transcendental. Moreover, we give sufficient conditions that 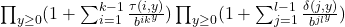 is transcendental.
is transcendental.
A primality test for Kpn + 1 numbers and a generalization of Safe primes and Sophie Germain primes
Original research paper. Pages 62–77
Abdelrahman Ramzy
Full paper (PDF, 335 Kb) | Abstract
In this paper, we provide a generalization of Proth’s theorem for integers of the form
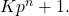
In particular, a primality test that requires a modular exponentiation (with a proper base

) similar to that of Fermat’s test without the computation of any GCD’s. We also provide two tests to increase the chances of proving the primality of
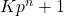
primes. As corollaries, we provide three families of integers
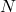
whose primality can be certified only by proving that
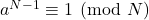
(Fermat’s test). One of these families is identical to Safe primes (since
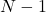
for these integers has large prime factor the same as Safe primes). Therefore, we considered them as a generalization of Safe primes and defined them as

-Safe primes. We address some questions regarding the distribution of those numbers and provide a conjecture about the distribution of their generative numbers

-Sophie Germain primes which seems to be true even if we are dealing with
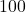
,
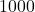
, or
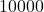
digits primes.
Sums involving the binomial coefficients, Bernoulli numbers of the second kind and harmonic numbers
Original research paper. Pages 78–97
Necdet Batır and Anthony Sofo
Full paper (PDF, 299 Kb) | Abstract
We offer a number of various finite and infinite sum identities involving the binomial coefficients, Bernoulli numbers of the second kind and harmonic numbers. For example, among many others, we prove
![Rendered by QuickLaTeX.com \[\displaystyle \sum_{k=0}^{n}\frac{(-1)^{k}h_{k}}{4^{k}} {{2k} \choose {k}}G_{n-k}=\frac{(-1)^{n-1}}{2^{2n-1}}{{2n-2} \choose {n-1}}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-d8a55db4281e9f43631243f9b2c0b991_l3.png)
and
![Rendered by QuickLaTeX.com \[\displaystyle \sum_{k=1}^{\infty}\frac{h_{k}}{k^{2}(2k-1)4^{k}} {{2k} \choose {k}}=2\pi +3\zeta(2)\log 2-3\zeta(2)-\frac{7}{2}\zeta(3),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-7686fb941e20c40fa5d553f9f1f548f5_l3.png)
where 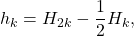
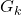 are Bernoulli numbers of the second kind, and
are Bernoulli numbers of the second kind, and 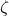 is the Riemann zeta function. We also give an alternate proof of the series representations for the constants
is the Riemann zeta function. We also give an alternate proof of the series representations for the constants 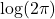 and
and 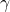 given by Blagouchine and Coppo.
given by Blagouchine and Coppo.
A generalized computation procedure for Ramanujan-type identities and cubic Shevelev sum
Original research paper. Pages 98–129
Peter J.-S. Shiue, Anthony G. Shannon, Shen C. Huang, Jorge E. Reyes
Full paper (PDF, 388 Kb) | Abstract
A generalized Computation procedure for construction of the Ramanujan-type from a given general cubic equation and a cosine Ramanujan-type identity is developed from detailed analyses of the properties of Ramanujan-type cubic equations. Examples are provided together with cubic Shevelev sums.
On certain equations and inequalities involving the arithmetical functions φ(n) and d(n) – II
Original research paper. Pages 130–136
József Sándor
Full paper (PDF, 229 Kb) | Abstract
In papers [3] and [5] we have studied certain equations and inequalities involving the arithmetical functions
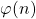
and
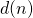
. In this paper we will consider some other equations. Some open problems will be stated, too.
Congruences for harmonic sums
Original research paper. Pages 137–146
Yining Yang and Peng Yang
Full paper (PDF, 237 Kb) | Abstract
Zhao found a curious congruence modulo
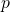
on harmonic sums. Xia and Cai generalized his congruence to a supercongruence modulo
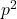
. In this paper, we improve the harmonic sums
![Rendered by QuickLaTeX.com \[ H_{p}(n)=\sum\limits_{\substack{l_{1}+l_{2}+\cdots+l_{n}=p\\ l_{1}, l_{2}, \ldots , l_{n}>0}} \frac{1}{l_{1} l_{2} \cdots l_{n}} \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-14ad129ba5296ac3f1728d6cf46703bf_l3.png)
to supercongruences modulo 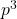 and
and 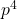 for odd and even where prime
for odd and even where prime 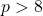 and
and 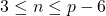 .
.
A note on edge irregularity strength of firefly graph
Original research paper. Pages 147–153
Umme Salma, H. M. Nagesh and D. Prahlad
Full paper (PDF, 1142 Kb) | Abstract
Let
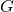
be a simple graph. A vertex labeling
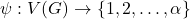
is called
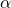
-labeling. For an edge
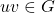
, the weight of
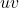
, written
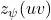
, is the sum of the labels of
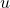
and

, i.e.,
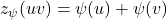
. A vertex
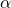
-labeling is said to be an edge irregular
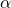
-labeling of
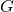
if for every two distinct edges

and
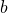
,
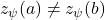
. The minimum
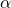
for which the graph
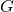
contains an edge irregular
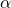
-labeling is known as the edge irregularity strength of
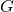
and is denoted by
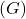
. In this paper, we find the exact value of edge irregularity strength of different cases of firefly graph
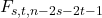
for any
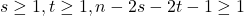
.
Hybrid hyper-Fibonacci and hyper-Lucas numbers
Original research paper. Pages 154–170
Yasemin Alp
Full paper (PDF, 311 Kb) | Abstract
Different number systems have been studied lately. Recently, many researchers have considered the hybrid numbers which are generalization of the complex, hyperbolic and dual number systems. In this paper, we define the hybrid hyper-Fibonacci and hyper-Lucas numbers. Furthermore, we obtain some algebraic properties of these numbers such as the recurrence relations, the generating functions, the Binet’s formulas, the summation formulas, the Catalan’s identity, the Cassini’s identity and the d’Ocagne’s identity.
Objects generated by an arbitrary natural number. Part 3: Standard modal-topological aspect
Original research paper. Pages 171–180
Krassimir Atanassov
Full paper (PDF, 262 Kb) | Abstract
The set
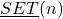
generated by an arbitrary natural number

, was defined in [3]. There, and in [4], some arithmetic functions and arithmetic operators of a modal type are defined over the elements of
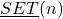
. Here, over the elements of
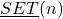
arithmetic operators of a topological type are defined and some of their basic properties are studied. Perspectives for future research are discussed.
Corrigendum to: “Some modular considerations regarding odd perfect numbers – Part II” [Notes on Number Theory and Discrete Mathematics, 2020, Vol. 26, No. 3, 8–24]
Corrigendum. Pages 181–184
Jose Arnaldo Bebita Dris and Immanuel Tobias San Diego
Full paper (PDF, 159 Kb) | Abstract
In [2], the authors proposed a theorem which they recently found out to contradict Chen and Luo’s results [1]. In the present paper, we provide the correct form of this theorem.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP4/30/2022.
Volume 29 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
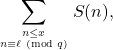
![]() denotes the number of non-isomorphic finite semisimple rings with
denotes the number of non-isomorphic finite semisimple rings with ![]() elements.
elements.![]() with
with ![]()
![]() is either rational or transcendental. Moreover, we give sufficient conditions that
is either rational or transcendental. Moreover, we give sufficient conditions that ![]() is transcendental.
is transcendental.![Rendered by QuickLaTeX.com \[\displaystyle \sum_{k=0}^{n}\frac{(-1)^{k}h_{k}}{4^{k}} {{2k} \choose {k}}G_{n-k}=\frac{(-1)^{n-1}}{2^{2n-1}}{{2n-2} \choose {n-1}}\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-d8a55db4281e9f43631243f9b2c0b991_l3.png)
![Rendered by QuickLaTeX.com \[\displaystyle \sum_{k=1}^{\infty}\frac{h_{k}}{k^{2}(2k-1)4^{k}} {{2k} \choose {k}}=2\pi +3\zeta(2)\log 2-3\zeta(2)-\frac{7}{2}\zeta(3),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-7686fb941e20c40fa5d553f9f1f548f5_l3.png)
![]()
![]() are Bernoulli numbers of the second kind, and
are Bernoulli numbers of the second kind, and ![]() is the Riemann zeta function. We also give an alternate proof of the series representations for the constants
is the Riemann zeta function. We also give an alternate proof of the series representations for the constants ![]() and
and ![]() given by Blagouchine and Coppo.
given by Blagouchine and Coppo.![Rendered by QuickLaTeX.com \[ H_{p}(n)=\sum\limits_{\substack{l_{1}+l_{2}+\cdots+l_{n}=p\\ l_{1}, l_{2}, \ldots , l_{n}>0}} \frac{1}{l_{1} l_{2} \cdots l_{n}} \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-14ad129ba5296ac3f1728d6cf46703bf_l3.png)
![]() and
and ![]() for odd and even where prime
for odd and even where prime ![]() and
and ![]() .
.

