Abdelrahman Ramzy
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 1, Pages 62–77
DOI: 10.7546/nntdm.2023.29.1.62-77
Full paper (PDF, 335 Kb)
Details
Authors and affiliations
Abdelrahman Ramzy ![]()
![]()
Department of Mathematics, Faculty of Education,
Al-Azhar University, Cairo, Egypt
Abstract
In this paper, we provide a generalization of Proth’s theorem for integers of the form ![]() In particular, a primality test that requires a modular exponentiation (with a proper base
In particular, a primality test that requires a modular exponentiation (with a proper base ![]() ) similar to that of Fermat’s test without the computation of any GCD’s. We also provide two tests to increase the chances of proving the primality of
) similar to that of Fermat’s test without the computation of any GCD’s. We also provide two tests to increase the chances of proving the primality of ![]() primes. As corollaries, we provide three families of integers
primes. As corollaries, we provide three families of integers ![]() whose primality can be certified only by proving that
whose primality can be certified only by proving that ![]() (Fermat’s test). One of these families is identical to Safe primes (since
(Fermat’s test). One of these families is identical to Safe primes (since ![]() for these integers has large prime factor the same as Safe primes). Therefore, we considered them as a generalization of Safe primes and defined them as
for these integers has large prime factor the same as Safe primes). Therefore, we considered them as a generalization of Safe primes and defined them as ![]() -Safe primes. We address some questions regarding the distribution of those numbers and provide a conjecture about the distribution of their generative numbers
-Safe primes. We address some questions regarding the distribution of those numbers and provide a conjecture about the distribution of their generative numbers ![]() -Sophie Germain primes which seems to be true even if we are dealing with
-Sophie Germain primes which seems to be true even if we are dealing with ![]() ,
, ![]() , or
, or ![]() digits primes.
digits primes.
Keywords
- Primality test
- Safe prime
- Sophie Germain prime
2020 Mathematics Subject Classification
- 11Y11
- 11N80
- 11N05
References
- Caldwell, C. K. (1997). An amazing prime heuristic. Preprint. Available online at: https://arxiv.org/abs/2103.04483v1.
- Grau, J. M., Oller-Marcén, A. M., & Sadornil, D. (2015). A primality test for
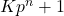 numbers, Mathematics of Computation, 84, 505–512.
numbers, Mathematics of Computation, 84, 505–512. - Hardy, G. H., & Littlewood J. E. (1923). Some problems of ‘partitio numerorum’ III. On the expression of a number as a sum of primes. Acta Mathematica, 44, 1–70.
- Korevaar, J. (2012). The prime pair conjecture of Hardy and Littlewood. Indagationes Mathematicae, 23, 269–299.
- Menezes, A. J., van Oorschot, P. C., & Vanstone, S. A. (1997). Handbook of Applied Cryptography. CRC Press, Boca Raton, FL.
- Ribenboim, P. (1996). The New Book Of Prime Number Records, 3rd ed. Springer, New York.
Manuscript history
- Received: 4 August 2022
- Revised: 6 January 2023
- Accepted: 19 February 2023
- Online First: 22 February 2023
Copyright information
![]() Ⓒ 2023 by the Author.
Ⓒ 2023 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Ramzy, A. (2023). A primality test for Kpn + 1 numbers and a generalization of Safe primes and Sophie Germain primes. Notes on Number Theory and Discrete Mathematics, 29(1), 62-77, DOI: 10.7546/nntdm.2023.29.1.62-77.


