Sibel Koparal, Neşe Ömür and Laid Elkhiri
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 29, 2023, Number 4, Pages 804–812
DOI: 10.7546/nntdm.2023.29.4.804-812
Full paper (PDF, 282 Kb)
Details
Authors and affiliations
Sibel Koparal ![]()
![]()
Department of Mathematics, University of Bursa Uludağ
16059 Nilufer, Bursa, Turkey
Neşe Ömür ![]()
![]()
Department of Mathematics, University of Kocaeli
41380 Izmit, Kocaeli, Turkey
Laid Elkhiri ![]()
![]()
Faculty of Material and Sciences, University of Tiaret
Algeria
Abstract
In this paper, we define generalized hyperharmonic numbers of order ![]() for
for ![]() and give some applications by using generating functions of these
and give some applications by using generating functions of these
numbers. For example, for ![]() such that
such that ![]()
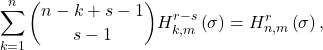
and
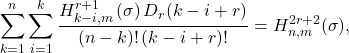
where ![]() is an
is an ![]() -derangement number.
-derangement number.
Keywords
- Sums
- Generalized harmonic numbers
- Generating function
2020 Mathematics Subject Classification
- 05A15
- 05A19
- 11B73
References
- Abouzahra, M., & Lewin, L. (1985). The polylogarithm in algebraic number fields. Journal of Number Theory, 21(2), 214–244.
- Adelberg, A. (2002). Kummer congruences for universal Bernoulli numbers and related congruences for poly-Bernoulli numbers. International Mathematical Journal, 1(1), 53–63.
- Choi, J., & Srivastava, H.M., (2011). Some summation formulas involving harmonic numbers and generalized harmonic numbers. Mathematical and Computer Modelling, 54, 2220–2234.
- Genčev, M. (2011). Binomial sums involving harmonic numbers. Mathematica Slovaca, 61(2), 215–226.
- Guo, D., & Chu, W. (2021). Summation formulae involving multiple harmonic numbers. Applicable Analysis and Discrete Mathematics, 15(1), 201–212.
- Koparal, S., Ömür, N., Sudemen, K.N. (2022). Some identities for derangement numbers. Miskolc Mathematical Notes, 23(2), 773–785.
- Ömür, N., & Koparal, S. (2022). Sums involving generalized harmonic and Daehee numbers. Notes on Number Theory and Discrete Mathematics, 28(1), 92–99.
- Ömür, N., & Bilgin, G. (2018). Some applications of the generalized hyperharmonic numbers of order
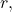
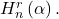 Advances and Applications in Mathematical Sciences, 17(9), 617–627.
Advances and Applications in Mathematical Sciences, 17(9), 617–627. - Ömür, N., & Koparal, S. (2018). On the matrices with the generalized hyperharmonic numbers of order r. Asian-European Journal of Mathematics, 11(3), Article ID 1850045.
- Spieß, J. (1990). Some identities involving harmonic numbers. Mathematics of Computation, 55(132), 839–863.
- Wang, C., Miska, P., & Mező, I. (2017). The r-derangement numbers. Discrete Mathematics, 340, 1681–1692.
Manuscript history
- Received: 26 February 2023
- Revised: 13 November 2023
- Accepted: 23 November 2023
- Online First: 30 November 2023
Copyright information
![]() Ⓒ 2023 by the Authors.
Ⓒ 2023 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Koparal, S., Ömür, N., & Elkhiri, L. (2023). On generalized hyperharmonic numbers of order ![]() . Notes on Number Theory and Discrete Mathematics, 29(4), 804-812, DOI: 10.7546/nntdm.2023.29.4.804-812.
. Notes on Number Theory and Discrete Mathematics, 29(4), 804-812, DOI: 10.7546/nntdm.2023.29.4.804-812.


