Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On the pulsating Padovan sequence
Original research paper. Pages 1–7
Orhan Dişkaya and Hamza Menken
Full paper (PDF, 182 Kb) | Abstract
A novel kind of Padovan sequence is introduced, and precise formulas for the form of its members are given and proven. Furthermore, the pulsating Padovan sequence in its most general form is introduced and the obtained identity is proved.
Discatenated and lacunary recurrences
Original research paper. Pages 8–19
Hakan Akkuş, Ömür Deveci, Engin Özkan and Anthony G. Shannon
Full paper (PDF, 944 Kb) | Abstract
Recursive sequences with gaps have been studied previously. This paper considers some elementary properties of such sequences where the gaps have been created on a regular basis from sequence to sequence – ‘discatenated’ (systematic gaps) and ‘lacunary’ (general gaps). In particular, their generating functions are developed in order to open up their general terms and relations with other properties.
Proving the existence of Euclidean knight’s tours on n × n × ⋯ × n chessboards for n < 4
Original research paper. Pages 20–33
Marco Ripà
Full paper (PDF, 1613 Kb) | Abstract
The Knight’s Tour problem consists of finding a Hamiltonian path for the knight on a given set of points so that the knight can visit exactly once every vertex of the mentioned set. In the present, we provide a 5-dimensional alternative to the well-known statement that it is not ever possible for a knight to visit once every vertex of
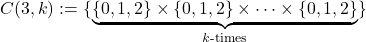
by performing a sequence of
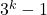
jumps of standard length, since the most accurate answer to the original question actually depends on which mathematical assumptions we are making at the beginning of the game when we decide to extend a planar chess piece to the third dimension and above.
Our counterintuitive outcome follows from the observation that we can alternatively define a 2D knight as a piece that moves from one square to another on the chessboard by covering a fixed Euclidean distance of
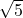
so that also the statement of Theorem 3 in [Erde, J., Golénia, B., & Golénia, S. (2012), The closed knight tour problem in higher dimensions, The Electronic Journal of Combinatorics, 19(4), #P9] does not hold anymore for such a Euclidean knight, as long as a 2 × 2 × ⋯ × 2 chessboard with at least 2
7 cells is given. Moreover, we construct a classical closed knight’s tour on
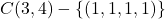
whose arrival is at a distance of 2 from
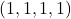
, and then we show a closed Euclidean knight’s tour on
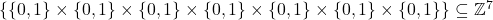
.
Some results on geometric circulant matrices involving the Leonardo numbers
Original research paper. Pages 34–46
Samet Arpacı and Fatih Yılmaz
Full paper (PDF, 316 Kb) | Abstract
In this study, by the motivation of the papers in the literature, we construct a special geometric circulant matrix
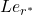
whose entries are the Leonardo numbers. Then, we investigate some linear algebraic properties of these matrices. More specifically, we present some bounds for the spectral norm, as well as Euclidean norm of this matrix form. For this purpose, we benefit from the spectacular properties of the Leonardo numbers. Furthermore, we throw light on the obtained results with examples. In addition to all these, we give two Matlab code in order to calculate the results related norms more easily and more accurately in a short time in the computer environment.
Second-order linear recurrences with identically distributed residues modulo pe
Original research paper. Pages 47–66
Lawrence Somer and Michal Křížek
Full paper (PDF, 257 Kb) | Abstract
Let

be an odd prime and let
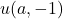
and
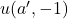
be two Lucas sequences whose discriminants have the same nonzero quadratic character modulo

and whose periods modulo

are equal. We prove that there is then an integer

such that for all
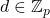
, the frequency with which
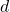
appears in a full period of
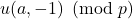
is the same frequency as
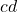
appears in
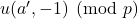
. Here
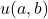
satisfies the recursion relation
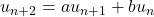
with initial terms
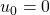
and
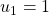
. Similar results are obtained for the companion Lucas sequences
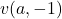
and
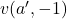
. This paper extends analogous statements for Lucas sequences of the form
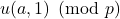
given in a previous article. We further generalize our results by showing for a certain class of primes

that if
,
, and
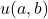
and
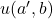
are Lucas sequences with the same period modulo

, then there exists an integer

such that for all residues
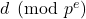
, the frequency with which
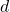
appears in
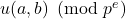
is the same frequency as
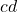
appears in
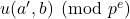
.
Generalization of the 2-Fibonacci sequences and their Binet formula
Original research paper. Pages 67–80
Timmy Ma, Richard Vernon and Gurdial Arora
Full paper (PDF, 256 Kb) | Abstract
We will explore the generalization of the four different 2-Fibonacci sequences defined by Atanassov. In particular, we will define recurrence relations to generate each part of a 2-Fibonacci sequence, discuss the generating function and Binet formula of each of these sequences, and provide the necessary and sufficient conditions to obtain each type of Binet formula.
Distance between consecutive elements of the multiplicative group of integers modulo n
Original research paper. Pages 81–99
Steven Brown
Full paper (PDF, 314 Kb) | Abstract
Some new properties of hyperbolic k-Fibonacci and k-Lucas octonions
Original research paper. Pages 100–110
A. D. Godase
Full paper (PDF, 218 Kb) | Abstract
The aim of this paper is to establish some novel identities for hyperbolic k-Fibonacci octonions and k-Lucas octonions. We prove these properties using the identities of k-Fibonacci and k-Lucas numbers, which we determined previously.
On certain arithmetical products involving the divisors of an integer
Original research paper. Pages 111–115
József Sándor
Full paper (PDF, 210 Kb) | Abstract
We study the arithmetical products
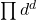
,
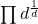
and
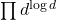
, where
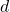
runs through the divisors of an integer
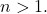
Sequences in finite fields yielding divisors of Mersenne, Fermat and Lehmer numbers, I
Original research paper. Pages 116–140
A. M. S. Ramasamy
Full paper (PDF, 347 Kb) | Abstract
The aim of this work is to present a method using the cyclic sequences
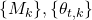
and
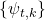
in the finite fields
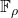
, with
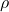
a prime, that yield divisors of Mersenne, Fermat and Lehmer numbers. The transformations
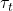
and
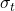
are introduced which lead to the proof of the cyclic nature of the sequences
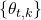
and
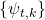
. Results on the roots of the
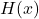
-polynomials in
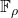
form the central theme of the study.
On the characterization of rectangular duals
Original research paper. Pages 141–149
Vinod Kumar and Krishnendra Shekhawat
Full paper (PDF, 181 Kb) | Abstract
A rectangular partition is a partition of a rectangle into a finite number of rectangles. A rectangular partition is generic if no four of its rectangles meet at the same point. A plane graph

is called a rectangularly dualizable graph if

can be represented as a rectangular partition such that each vertex is represented by a rectangle in the partition and each edge is represented by a common boundary segment shared by the corresponding rectangles. Then the rectangular partition is called a rectangular dual of the RDG. In this paper, we have found a minor error in a characterization for rectangular duals given by Koźmiński and Kinnen in 1985 without formal proof, and we fix this characterization with formal proof.
Generalized perfect numerical semigroups
Original research paper. Pages 150–162
Mohammad Zmmo and Nesrin Tutaş
Full paper (PDF, 461 Kb) | Abstract
In this work, we study the isolated gaps for generalized numerical semigroups, introduce generalized perfect numerical semigroups, and exemplify these semigroups. In particular, we reveal the effects of the perfectness condition on a generalized Weierstrass semigroup.
Characterization of prime and composite numbers using the notion of successive sum of integers and the consequence in primality testing
Original research paper. Pages 163–169
Fateh Mustapha Dehmeche, Douadi Mihoubi and Lahcene Ladjelat
Full paper (PDF, 579 Kb) | Abstract
In this paper, we give a characterization of primes and composite natural numbers using the notion of the sum of successive natural numbers. We prove essentially that an odd natural number

is prime if and only if the unique decomposition of
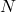
as a sum of successive natural numbers is the trivial decomposition
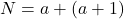
with
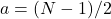
.
Factorial polynomials and associated number families
Original research paper. Pages 170–178
Alfred Schreiber
Full paper (PDF, 195 Kb) | Abstract
Two doubly indexed families of polynomials in several indeterminates are considered. They are related to the falling and rising factorials in a similar way as the potential polynomials (introduced by L. Comtet) are related to the ordinary power function. We study the inversion relations valid for these factorial polynomials as well as the number families associated with them.
Two arithmetic functions related to Euler’s and Dedekind’s functions
Original research paper. Pages 179–183
Krassimir Atanassov
Full paper (PDF, 225 Kb) | Abstract
Two new arithmetic functions are introduced. In some sense, they are modifications of Euler’s and Dedekind’s functions. Some properties of the new functions are studied.
Metallic means and Pythagorean triples
Original research paper. Pages 184–194
Chetansing Rajput and Hariprasad Manjunath
Full paper (PDF, 359 Kb) | Abstract
In this article, we study the connection between Pythagorean triples and metallic means. We derive several interconnecting identities between different metallic means. We study the Pythagorean triples in the three-term recurrent sequences corresponding to different metallic means. Further, we relate different families of primitive Pythagorean triples to the corresponding metallic means.
Distribution of constant terms of irreducible polynomials in ℤp[x] whose degree is a product of two distinct odd primes
Original research paper. Pages 195–210
Sarah C. Cobb, Michelle L. Knox, Marcos Lopez, Terry McDonald, and Patrick Mitchell
Full paper (PDF, 280 Kb) | Abstract
We obtain explicit formulas for the number of monic irreducible polynomials with prescribed constant term and degree
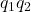
over a finite field, where
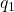
and
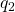
are distinct odd~primes. These formulas are derived from work done by Yucas. We show that the number of polynomials of a given constant term depends only on whether the constant term is a
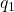
-residue and/or a
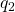
-residue in the underlying field. We further show that as

becomes large, the proportion of irreducible polynomials having each constant term is asymptotically equal. This paper continues work done in [1].
Editorial Correction to “A note on a generalization of Riordan’s combinatorial identity via a hypergeometric series approach” [Notes on Number Theory and Discrete Mathematics, 2023, Volume 29, Number 3, Pages 421–425]
Editorial correction. Pages 211–212
Kunle Adegoke
Editorial correction (PDF, 161 Kb)
Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() in
in ![]() which we note
which we note ![]() . This work, presented with different notations is closely related to [5]. We prove the formulas in three steps. Although only the last step relates to the problem of gaps in the Eratosthenes sieve (see Section 3.2.2) the previous formulas may be of interest to study occurrences of defined gaps sequences.
. This work, presented with different notations is closely related to [5]. We prove the formulas in three steps. Although only the last step relates to the problem of gaps in the Eratosthenes sieve (see Section 3.2.2) the previous formulas may be of interest to study occurrences of defined gaps sequences. , we prove a general formula based on the inclusion-exclusion principle to count the number of occurrences of configurations1 in any subset of
, we prove a general formula based on the inclusion-exclusion principle to count the number of occurrences of configurations1 in any subset of 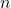 . (see Equation (7) in Theorem 2.1).
. (see Equation (7) in Theorem 2.1).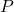 , we particularize this formula when the subset of interest is
, we particularize this formula when the subset of interest is 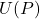 . (see Equation (11) in Theorem 3.2).
. (see Equation (11) in Theorem 3.2). and its primorial
and its primorial 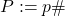 , we particularize the formula again to study gaps in
, we particularize the formula again to study gaps in 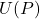 . Given a positive integer
. Given a positive integer 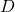 representing a distance on the circle, we give formulas to count
representing a distance on the circle, we give formulas to count 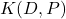 the number of gaps of length
the number of gaps of length 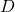 between elements of
between elements of 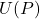 (see Equation (15) and Section 4.1).
(see Equation (15) and Section 4.1).![]() that contain exactly
that contain exactly ![]() elements of
elements of ![]() .
.

