Steven Brown
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 1, Pages 81–99
DOI: 10.7546/nntdm.2024.30.1.81-99
Full paper (PDF, 314 Kb)
Details
Authors and affiliations
Steven Brown ![]()
![]()
41 Boulevard du Roi, 78000 Versailles, France
Abstract
For a prime number ![]() , we consider its primorial
, we consider its primorial ![]() and
and ![]() the set of elements of the multiplicative group of integers modulo
the set of elements of the multiplicative group of integers modulo ![]() which we represent as points anticlockwise on a circle of perimeter
which we represent as points anticlockwise on a circle of perimeter ![]() . These points considered with wrap around modulo
. These points considered with wrap around modulo ![]() are those not marked by the Eratosthenes sieve algorithm applied to all primes less than or equal to
are those not marked by the Eratosthenes sieve algorithm applied to all primes less than or equal to ![]() .
.
In this paper, we are mostly concerned with providing formulas to count the number of gaps of a given even length ![]() in
in ![]() which we note
which we note ![]() . This work, presented with different notations is closely related to [5]. We prove the formulas in three steps. Although only the last step relates to the problem of gaps in the Eratosthenes sieve (see Section 3.2.2) the previous formulas may be of interest to study occurrences of defined gaps sequences.
. This work, presented with different notations is closely related to [5]. We prove the formulas in three steps. Although only the last step relates to the problem of gaps in the Eratosthenes sieve (see Section 3.2.2) the previous formulas may be of interest to study occurrences of defined gaps sequences.
- For a positive integer
 , we prove a general formula based on the inclusion-exclusion principle to count the number of occurrences of configurations1 in any subset of
, we prove a general formula based on the inclusion-exclusion principle to count the number of occurrences of configurations1 in any subset of 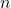 . (see Equation (7) in Theorem 2.1).
. (see Equation (7) in Theorem 2.1). - For a square-free integer
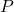 , we particularize this formula when the subset of interest is
, we particularize this formula when the subset of interest is 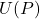 . (see Equation (11) in Theorem 3.2).
. (see Equation (11) in Theorem 3.2). - For a prime
 and its primorial
and its primorial 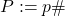 , we particularize the formula again to study gaps in
, we particularize the formula again to study gaps in 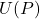 . Given a positive integer
. Given a positive integer 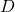 representing a distance on the circle, we give formulas to count
representing a distance on the circle, we give formulas to count 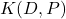 the number of gaps of length
the number of gaps of length 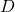 between elements of
between elements of 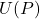 (see Equation (15) and Section 4.1).
(see Equation (15) and Section 4.1).
In addition, we provide a formula (see Equation (27) in Theorem 5.1) to count the number of occurrences of gaps of an even length ![]() that contain exactly
that contain exactly ![]() elements of
elements of ![]() .
.
1 A defined sequence of gaps between the elements of the subset; this is referred to as a constellation in [5].
Keywords
- Sieves
- Sieve of Eratosthenes
- Modular arithmetic
- Multiplicative group of integers modulo
- Chinese remainder theorem
- Inclusion-exclusion principle
- Euler’s phi function
- Nagell’s totient function
- Prime numbers
- Jacobsthal function
- Primorial
2020 Mathematics Subject Classification
- 11A07
- 11A41
- 11B99
- 11N05
- 11N35
- 11N99
- 03E99
References
- Andreescu, T., & Andrica, D. (2009). Number Theory: Structures, Examples, and Problems. Birkhauser.
- Cohen, E. (1960). Nagell’s totient function. Mathematica Scandinavica, 8(1), 55–58.
- Hardy, G. H., & Wright, E. M. (1979). An Introduction to the Theory of Numbers. Oxford University Press.
- Haukkanen, P., & Sivaramakrishnan, R. (1998). Nagell’s totient revisited. Notes on Number Theory and Discrete Mathematics, 4(3), 93–100.
- Holt, F. B. (2015). Combinatorics of the gaps between primes. Preprint. arXiv:1510.00743.
- Iwaniec, H. (1978). On the problem of Jacobsthal. Demonstratio Mathematica, 11(1), 225–232.
- OEIS Foundation Inc. (2023). The On-Line Encyclopedia of Integer Sequences. Available online at: https://oeis.org.
- Tarnauceanu, M. (2013). A generalization of the Euler’s totient function. Preprint. arXiv:1312.1428.
- Van Hamme, L. (1971). Sur une gen eralisation de l’indicateur d’Euler. Bulletins de l’Academie Royale de Belgique, 57(1), 805–817.
- Weisstein, E. W. (2009). Landau’s Problems. Available online at: https://
mathworld.wolfram.com/. - Ziller, M. (2020). On differences between consecutive numbers coprime to primorials. Preprint. arXiv:2007.01808.
Manuscript history
- Received: 2 October 2023
- Revised: 12 December 2024
- Accepted: 11 February 2024
- Online First: 29 February 2024
Copyright information
![]() Ⓒ 2024 by the Author.
Ⓒ 2024 by the Author.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
- Haukkanen, P., & Sivaramakrishnan, R. (1998). Nagell’s totient revisited. Notes on Number Theory and Discrete Mathematics, 4(3), 93–100.
Cite this paper
Brown, S. (2024). Distance between consecutive elements of the multiplicative group of integers modulo n. Notes on Number Theory and Discrete Mathematics, 30(1), 81-99, DOI: 10.7546/nntdm.2024.30.1.81-99.


