Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On recurrence results from matrix transforms
Original research paper. Pages 589–592
Ömür Deveci and Anthony G. Shannon
Full paper (PDF, 693 Kb) | Abstract
In this paper, the Laplace transform and various matrix operations are applied to the characteristic polynomial of the Fibonacci numbers. From this is generated some properties of the Jacobsthal numbers, including triangles where the row sums are known sequences. In turn these produce some new properties.
On a new class of the generalized Gauss k-Pell numbers and their polynomials
Original research paper. Pages 593–602
Ahmet Kaya and Hayrullah Özimamoğlu
Full paper (PDF, 174 Kb) | Abstract
In this article, we generalize the well-known Gauss Pell numbers and refer to them as generalized Gauss k-Pell numbers. There are relationships discovered between the class of generalized Gauss k-Pell numbers and the typical Gauss Pell numbers. Also, we generalize the known Gauss Pell polynomials, and call such polynomials as the generalized Gauss k-Pell polynomials. We obtain relations between the class of the generalized Gauss k-Pell polynomials and the typical Gauss Pell polynomials. Furthermore, we provide matrices for the novel generalizations of these numbers and polynomials. After that, we obtain Cassini’s identities for these numbers and polynomials.
Some multiple Dirichlet series of completely multiplicative arithmetic functions
Original research paper. Pages 603–616
Nabil Tahmi and Abdallah Derbal
Full paper (PDF, 216 Kb) | Abstract
Let
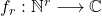
be an arithmetic function of

variables, where
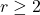
. We study multiple Dirichlet series defined by
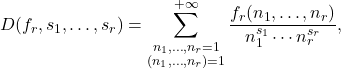
where 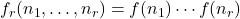 and
and 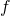 is a completely multiplicative or a specially multiplicative arithmetic function of a single variable. We obtain formulas for these series expressed by infinite products over the primes. We also consider the cases of certain particular completely multiplicative and specially multiplicative functions.
is a completely multiplicative or a specially multiplicative arithmetic function of a single variable. We obtain formulas for these series expressed by infinite products over the primes. We also consider the cases of certain particular completely multiplicative and specially multiplicative functions.
Asymptotics of sums of divisor functions over sequences with restricted factorization structure
Original research paper. Pages 617–634
Rafael Jakimczuk and Matilde Lalín
Full paper (PDF, 235 Kb) | Abstract
We compute asymptotics of the sums of general divisor functions over h-free numbers, h-full numbers and other arithmetically interesting sets and conditions. The main tool for obtaining these results is Perron’s formula.
Hook type tableaux and partition identities
Original research paper. Pages 635–647
Koustav Banerjee and Manosij Ghosh Dastidar
Full paper (PDF, 205 Kb) | Abstract
In this paper we exhibit the box-stacking principle (BSP) in conjunction with Young diagrams to prove generalizations of Stanley’s and Elder’s theorems without even the use of partition statistics in general. We primarily focus on to study Stanley’s theorem in color partition context.
Asymptotic formula of a “hyperbolic” summation related to the Piltz divisor function
Original research paper. Pages 648–655
Mihoub Bouderbala and Meselem Karras
Full paper (PDF, 216 Kb) | Abstract
Arithmetical functions associated with conjugate pairs of sets under regular convolutions
Original research paper. Pages 656–665
Pentti Haukkanen
Full paper (PDF, 179 Kb) | Abstract
Two subsets P and Q of the set of positive integers is said to form a conjugate pair if each positive integer n possesses a unique factorization of the form n = ab, a ∈ P, b ∈ Q. In this paper we generalize conjugate pairs of sets to the setting of regular convolutions and study associated arithmetical functions. Particular attention is paid to arithmetical functions associated with k-free integers and k-th powers under regular convolution.
New type degenerate Stirling numbers and Bell polynomials
Original research paper. Pages 666–676
Hye Kyung Kim
Full paper (PDF, 185 Kb) | Abstract
In this paper, we introduce a new type degenerate Stirling numbers of the second kind and their degenerate Bell polynomials, which is different from degenerate Stirling numbers of the second kind studied so far. We investigate the explicit formula, recurrence relation and Dobinski-like formula of a new type degenerate Stirling numbers of the second kind. We also derived several interesting expressions and identities for bell polynomials of these new type degenerate Stirling numbers of the second kind including the generating function, recurrence relation, differential equation with Bernoulli number as coefficients, the derivative and Riemann integral, so on.
Equations of two sets of consecutive square sums
Original research paper. Pages 677–691
P. J. Bush and K. V. Murphy
Full paper (PDF, 186 Kb) | Abstract
In this paper we investigate equations featuring sums of consecutive square integers, such as
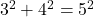
, and
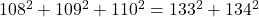
. In general, for a sum of
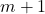
consecutive square integers,
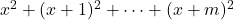
, there is a distinct set of
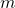
consecutive squares,
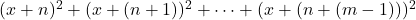
, to which these are equal. We present a bootstrap method for constructing these equations, which yields solutions comprising an infinite two-dimensional array. We apply a similar method to constructing consecutive square sum equations involving
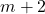
terms on the left, and
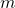
terms on the right, formed from two distinct sets of consecutive squares separated one term to the left of the equals sign, such as
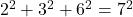
.
On a generalization of a function of J. Sándor
Original research paper. Pages 692–697
V. Siva Rama Prasad and P. Anantha Reddy
Full paper (PDF, 198 Kb) | Abstract
Using a strictly increasing function
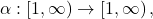
we define below (see(1.1) and (1.2)) two functions
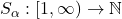
and
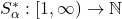
, where
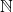
is the set of all natural numbers. The functions
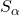
and
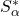
respectively generalize the functions
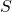
and
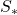
introduced and studied by J. Sándor [5] as well as the functions

and
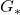
considered by N. Anitha [1]. In this paper we obtain several properties of
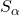
and
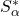
– some of which give the results of Sándor [5] and of Anitha [1] as special cases.
Linear mappings in paraletrix spaces and their application to fractional calculus
Original research paper. Pages 698–709
R. U. Ndubuisi, U. K. Nwajeri, C. P. Onyenegecha, K. M. Patil, O. G. Udoaka and W. I. Osuji
Full paper (PDF, 549 Kb) | Abstract
This paper considers linear mappings in paraletrix spaces as an extension of the one given for rhotrix vector spaces. Furthermore, the adjoints of these mappings are given with their application in fractional calculus.
On Vandiver’s arithmetical function – II
Original research paper. Pages 710–718
József Sándor
Full paper (PDF, 201 Kb) | Abstract
We study more properties of Vandiver’s arithmetical function
![Rendered by QuickLaTeX.com \[V(n) = \displaystyle \prod_{d\mid n} (d+1),\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-289cf8dc2a2eb0291785fb9aa21f89e2_l3.png)
introduced in [2].
Congruences via umbral calculus
Original research paper. Pages 719–729
Abdelkader Benyattou
Full paper (PDF, 193 Kb) | Abstract
In this paper, we use the properties of the classical umbral calculus to give some congruences related to the Bell numbers and Bell polynomials. We also present a new congruence involving Appell polynomials with integer coefficients.
Counting general power residues
Original research paper. Pages 730–743
Samer Seraj
Full paper (PDF, 197 Kb) | Abstract
Suppose every integer is taken to the power of a fixed integer exponent k ≥ 2 and the remainders of these powers upon division by a fixed integer n ≥ 2 are found. It is natural to ask how many distinct remainders are produced. By building on the work of Stangl, who published the k = 2 case in Mathematics Magazine in 1996, we find essentially closed formulas that allow for the computation of this number for any k. Along the way, we provide an exposition of classical results on the multiplicativity of this counting function and results on the number of remainders that are coprime to the modulus n.
Explicit formulas for sums related to Dirichlet L-functions
Original research paper. Pages 744–748
Brahim Mittou
Full paper (PDF, 182 Kb) | Abstract
Let
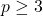
be a prime number and let
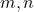
and
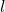
be integers with
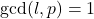
. Let
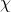
be a Dirichlet character modulo

and
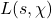
be the Dirichlet L-function corresponding to
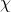
. Explicit formulas for:
![Rendered by QuickLaTeX.com \[\dfrac{2}{p-1} \sum \limits\sb{\underset{\chi(-1)=+1}{\chi\hspace{-0.2cm} \mod p}} \chi(l) L(m,\chi)L(n,\overline{\chi}) \text{ and }\dfrac{2}{p-1} \sum \limits\sb{\underset{\chi(-1)=-1}{\chi\hspace{-0.2cm} \mod p}} \chi(l) L(m,\chi)L(n,\overline{\chi})\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a5e3dbf7bb50c15e8f39da1061e119c2_l3.png)
are given in this paper by using the properties of character sums and Bernoulli polynomials.
The integrality of the Genocchi numbers obtained through a new identity and other results
Original research paper. Pages 749–757
Bakir Farhi
Full paper (PDF, 199 Kb) | Abstract
In this note, we investigate some properties of the integer sequence of general term
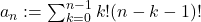
(
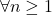
) to derive a new identity of the Genocchi numbers
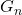
(
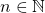
), which immediately shows that
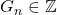
for any
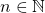
. In another direction, we obtain nontrivial lower bounds for the
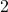
-adic valuations of the rational numbers
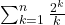
.
On combined 3-Fibonacci sequences
Original research paper. Pages 758–764
Krassimir T. Atanassov, Lilija C. Atanassova and Anthony G. Shannon
Full paper (PDF, 145 Kb) | Abstract
The term ‘combined’ sequence includes any of the ‘coupled’, ‘intercalated’ and ‘pulsated’ sequences. In this paper,
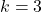
, so new combined
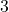
-Fibonacci sequences,
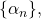
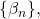
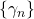
, are introduced and the explicit formulae for their general terms are developed. That is, there are three such sequences, each with a linear recurrence relation which contains terms from the other two. In effect, each such recurrence relation is second order, with two initial terms which specify the subsequent delineation of the terms of the sequences. The initial terms are, respectively,
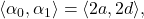
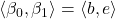
and
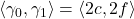
in turn. These result in neat inter-relationships among the three sequences, which can lead to intriguing connections with known sequences, and to a surprisingly simple graphical representation of the whole process. The references include a comprehensive cover of the pertinent literature on these aspects of recursive sequences particularly during the last seventy years.
A secondary goal of the paper is to put the disarray of this part of number theory into some semblance of order with a selection of representative references. This gives rise to a ‘combobulated sequence’, so-called because it restores partial order to a disarray of many papers into three classes, which are fuzzy in both their membership and non-membership because of their diverse and non-systematic derivations.
On generalized (k, r)-Pell and (k, r)-Pell–Lucas numbers
Original research paper. Pages 765–777
Bahar Kuloğlu and Engin Özkan
Full paper (PDF, 273 Kb) | Abstract
We introduce new kinds of

-Pell and

-Pell–Lucas numbers related to the distance between numbers by a recurrence relation and show their relation to the
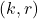
-Pell and
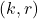
-Pell–Lucas numbers. These sequences differ both according to the value of the natural number

and the value of a new parameter

in the definition of this distance. We give several properties of these sequences. In addition, we establish the generating functions, some important identities, as well as the sum of the terms of the generalized
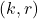
-Pell and
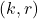
-Pell–Lucas numbers. Furthermore, we indicate another way to obtain the generalized
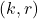
-Pell and
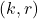
-Pell–Lucas sequences from the generating function, in connection to graphs.
Combinatorial proofs of identities for the generalized Leonardo numbers
Original research paper. Pages 778–790
Mark Shattuck
Full paper (PDF, 210 Kb) | Abstract
In this paper, we provide combinatorial proofs of several prior identities satisfied by the recently introduced generalized Leonardo numbers, denoted by
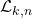
, as well as derive some new formulas. To do so, we interpret
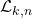
as the enumerator of two classes of linear colored tilings of length

. A comparable treatment is also given for the incomplete generalized Leonardo numbers. Finally, a
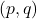
-generalization of
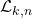
is obtained by considering the joint distribution of a pair of statistics on one of the aforementioned classes of colored tilings.
In Memoriam: Prof. John Turner (1928 – 2022)
Editorial. Pages 791–793
Anthony G. Shannon
Editorial (PDF, 532 Kb)
Book review: “The Possibly True Story of Martin Gardiner”
Book review. Pages 794–795
Anthony G. Shannon
Book review (PDF, 600 Kb)
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP3/43/2021.
Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
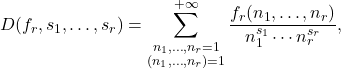
![]() and
and ![]() is a completely multiplicative or a specially multiplicative arithmetic function of a single variable. We obtain formulas for these series expressed by infinite products over the primes. We also consider the cases of certain particular completely multiplicative and specially multiplicative functions.
is a completely multiplicative or a specially multiplicative arithmetic function of a single variable. We obtain formulas for these series expressed by infinite products over the primes. We also consider the cases of certain particular completely multiplicative and specially multiplicative functions.![]()
![]() , where
, where ![]() denotes the Piltz divisor function, and
denotes the Piltz divisor function, and ![]() is the unitary analogue function of
is the unitary analogue function of ![]() .
.![]()
![Rendered by QuickLaTeX.com \[\dfrac{2}{p-1} \sum \limits\sb{\underset{\chi(-1)=+1}{\chi\hspace{-0.2cm} \mod p}} \chi(l) L(m,\chi)L(n,\overline{\chi}) \text{ and }\dfrac{2}{p-1} \sum \limits\sb{\underset{\chi(-1)=-1}{\chi\hspace{-0.2cm} \mod p}} \chi(l) L(m,\chi)L(n,\overline{\chi})\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a5e3dbf7bb50c15e8f39da1061e119c2_l3.png)


