Volume 27 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Multiplicative functions satisfying the functional equation κf(m2+n2) = f(κm2) + f(κn2)
Original research paper. Pages 1–11
Wuttichai Suriyacharoen and Vichian Laohakosol
Full paper (PDF, 206 Kb) | Abstract
For a fixed positive integer
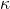
, the functional equation
![Rendered by QuickLaTeX.com \[\kappa f(m^2 + n^2) = f(\kappa m^2) + \kappa f(n^2)\qquad(m,n\in\mathbb{N})\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-04e7e4da2dd54cc9da4c6b7f4d19c3fb_l3.png)
is solved for multiplicative functions 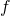 . This complements a 1996 result of Chung [2] which deals with the case
. This complements a 1996 result of Chung [2] which deals with the case 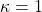 . The method used relies on the sum of two squares theorem in number theory.
. The method used relies on the sum of two squares theorem in number theory.
A short remark on an arithmetic function
Original research paper. Pages 12–15
Anthony G. Shannon and Krassimir T. Atanassov
Full paper (PDF, 154 Kb) | Abstract
An explicit form of A. Shannon’s arithmetic function δ is given. A possible application of it is discussed for representation of the well-known arithmetic functions ω and Kronecker’s delta-function δm,s.
On the average order of the gcd-sum function over arbitrary sets of integers
Original research paper. Pages 16–28
V. Siva Rama Prasad and P. Anantha Reddy
Full paper (PDF, 244 Kb) | Abstract
Let
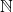
denote the set of all positive integers and for
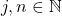
, let
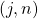
denote their greatest common divisor. For any
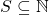
, we define
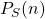
to be the sum of those
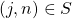
, where
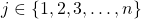
. An asymptotic formula for the summatory function of
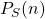
is obtained in this paper which is applicable to a variety of sets
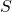
. Also the formula given by Bordellès for the summatory function of
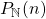
can be derived from our result. Further, depending on the structure of
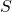
, the asymptotic formulae obtained from our theorem give better error terms than those deducible from a theorem of Bordellès (see Remark 4.4).
On Vandiver’s arithmetical function – I
Original research paper. Pages 29–38
József Sándor
Full paper (PDF, 218 Kb) | Abstract
We study certain properties of Vandiver’s arithmetic function
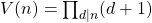
.
Note on translated sum on primitive sequences
Original research paper. Pages 39–43
Ilias Laib
Full paper (PDF, 189 Kb) | Abstract
In this note, we construct a new set
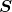
of primitive sets such that for any real number

we get:
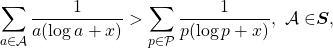
where 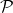 denotes the set of prime numbers.
denotes the set of prime numbers.
Fibonacci series from power series
Original research paper. Pages 44–62
Kunle Adegoke
Full paper (PDF, 214 Kb) | Abstract
We show how every power series gives rise to a Fibonacci series and a companion series involving Lucas numbers. For illustrative purposes, Fibonacci series arising from trigonometric functions, the gamma function and the digamma function are derived. Infinite series involving Fibonacci and Bernoulli numbers and Fibonacci and Euler numbers are also obtained.
On some 3 × 3 dimensional matrices associated with generalized Fibonacci numbers
Original research paper. Pages 63–72
Halim Özdemir, Sinan Karakaya and Tuğba Petik
Full paper (PDF, 209 Kb) | Abstract
In this work, it is presented a procedure to find some 3 × 3 dimensional matrices whose integer powers can be characterized by generalized Fibonacci numbers. Moreover, some numerical examples are given to exemplify the procedure established.
A note on ratios of Fibonacci hybrid and Lucas hybrid numbers
Original research paper. Pages 73–78
Emrah Polatlı
Full paper (PDF, 148 Kb) | Abstract
Irmak recently asked an open question related to divisibility properties of Fibonacci and Lucas quaternions [4, p. 374]. In this paper, we give an answer to Fibonacci and Lucas hybrid number version of this question.
On evolving chains of cube-free binary sequences
Original research paper. Pages 79–94
Jacek M. Kowalski and Andrzej Pękalski
Full paper (PDF, 217 Kb) | Abstract
Chains of concatenated finite binary words are considered, where each word, except possibly the very first one, is composed of alternating blocks of zeroes and ones with block lengths not exceeding two. These chains are formed following two evolution schemes. The first scheme is standard, where alternating blocks are visited at random. In the second approach, proposed by us in this paper, each subsequent word of the chain is uniquely determined by its immediate predecessor, being formed as a specifically inflated version of that word. Famous Kolakoski sequence is then just one, very special example of such deterministic evolution when one starts from its third element. We present heuristic arguments supported by simulations indicating that all such deterministic infinite chains should have the asymptotic density of digit
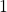
equal
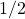
and that the subsequent word lengths asymptotically scale with factor of
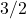
and hence the density of
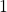
’s in subsequent finite words may also tend to
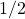
.
De Moivre-type identities for the Jacobsthal numbers
Original research paper. Pages 95–103
Mücahit Akbiyik and Seda Yamaç Akbiyik
Full paper (PDF, 157 Kb) | Abstract
The main aim of this study is to obtain De Moivre-type identities for Jacobsthal numbers. Also, this paper presents a method for constructing the second order Jacobsthal and Jacobsthal third-order numbers and the third-order Jacobsthal and Jacobsthal–Lucas numbers. Moreover, we give some interesting identities, such as Binet’s formulas for some specific third-order Jacobsthal numbers that we derive from De Moivre-type identities.
Heilbronn-like sums and their properties
Original research paper. Pages 104–112
H. Saydi and M. R. Darafsheh
Full paper (PDF, 227 Kb) | Abstract
Heilbronn sums is of the form
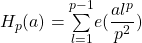
, where

is an odd prime, and
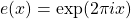
. This is a supercharacter and has application in number theory. We extend this sum by defining
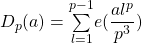
, where

is an odd prime and prove that
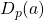
is a supercharacter and drive a few identities involving
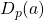
.
A Diophantine equation about polygonal numbers
Original research paper. Pages 113–118
Yangcheng Li
Full paper (PDF, 206 Kb) | Abstract
It is well known that the number
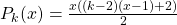
is called the
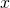
-th

-gonal number, where
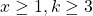
. Many Diophantine equations about polygonal numbers have been studied. By the theory of Pell equation, we show that if
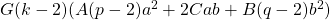
is a positive integer but not a perfect square,
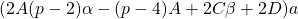
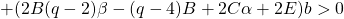
,
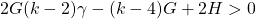
and the Diophantine equation
![Rendered by QuickLaTeX.com \[AP_p(x)+BP_q(y)+Cxy+Dx+Ey+F=GP_k(z)+Hz\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-723e7871609fedcaf225f0d11caa6f41_l3.png)
has a nonnegative integer solution 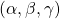 , then it has infinitely many positive integer solutions of the form
, then it has infinitely many positive integer solutions of the form 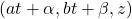 , where
, where 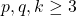 and
and 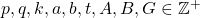 ,
, 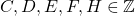 .
.
Perron numbers that satisfy Fermat’s equation
Original research paper. Pages 119–122
Pietro Paparella
Full paper (PDF, 146 Kb) | Abstract
In this note, it is shown that if
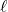
and
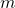
are positive integers such that

, then there is a
Perron number 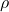
such that
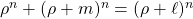
. It is also shown that there is an aperiodic integer matrix
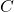
such that
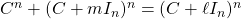
.
A note on the polynomial-exponential Diophantine equation
(an − 1)(bn − 1) = x2
Original research paper. Pages 123–129
Yasutsugu Fujita and Maohua Le
Full paper (PDF, 186 Kb) | Abstract
For any positive integer
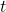
, let ord
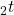
denote the order of
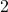
in the factorization of
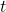
. Let
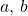
be two distinct fixed positive integers with
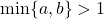
. In this paper, using some elementary number theory methods, the existence of positive integer solutions
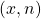
of the polynomial-exponential Diophantine equation
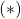
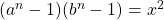
with
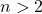
is discussed. We prove that if
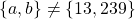
and ord
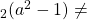
ord
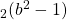
, then
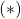
has no solutions
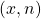
with
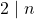
. Thus it can be seen that if
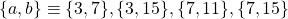
or
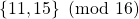
, where
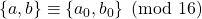
means either
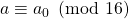
and
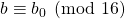
or
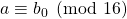
and
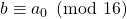
, then
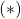
has no solutions
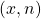
.
On the rational solutions of y2 =x3 + k6n+3
Original research paper. Pages 130–142
Richa Sharma and Sanjay Bhatter
Full paper (PDF, 218 Kb) | Abstract
We consider a family of elliptic curves
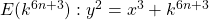
for some integers

and
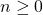
and prove that their rank is zero and the torsion part is isomorphic to
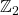
. This is an extension of a recent work of Wu and Qin [14].
Arithmetical functions commutable with sums of squares
Original research paper. Pages 143–154
I. Kátai and B. M. Phong
Full paper (PDF, 177 Kb) | Abstract
Let
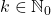
and
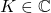
, where
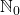
,
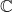
denote the set of nonnegative integers and complex numbers, respectively. We give all functions
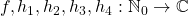
which satisfy the relation
![Rendered by QuickLaTeX.com \[f(x_1^2+x_2^2+x_3^2+x_4^2+k)=h_1(x_1)+h_2(x_2)+h_3(x_3)+h_4(x_4)+K\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-75d1198e024fd343cdb2d0c312edb97e_l3.png)
for every 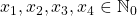 . We also give all arithmetical functions
. We also give all arithmetical functions 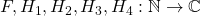 which satisfy the relation
which satisfy the relation
![Rendered by QuickLaTeX.com \[F(x_1^2+x_2^2+x_3^2+x_4^2+k)=H_1(x_1)+H_2(x_2)+H_3(x_3)+H_4(x_4)+K\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-837e49fc47bbeda8a88bca6006ce46a7_l3.png)
for every 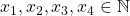 , where
, where 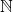 denotes the set of all positive integers.
denotes the set of all positive integers.
On Ramanujan type identities and Cardano formula
Original research paper. Pages 155–174
Kai Wang
Full paper (PDF, 220 Kb) | Abstract
In this paper we will prove some Ramanujan type identities such as
![Rendered by QuickLaTeX.com \begin{align*} &\sqrt[3]{\sin\left(\frac{\pi}{9}\right)} + \sqrt[3]{\sin\left(\frac{2\pi}{9}\right)} + \sqrt[3]{\sin\left(\frac{14\pi}{9}\right)} \\ & = \left(-\frac{\sqrt[18]{3}}{2}\right) \left(\sqrt[3]{6+3\left(\sqrt[3]{6-3\sqrt[3]{9}}+ \sqrt[3]{3-3\sqrt[3]{9}}\right)}\right), \end{align*}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-2cfc2e8bb6884536753c45ead504214c_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} &\sqrt[3]{\tan\left(\frac{\pi}{9}\right)} + \sqrt[3]{\tan\left(\frac{4\pi}{9}\right)} + \sqrt[3]{\tan\left(\frac{7\pi}{9}\right)} \\ & = \left(-\sqrt[18]{3}\right) \left(\sqrt[3]{-3\sqrt[3]{3}+6+3(\sqrt[3]{\!21 - 3(3\sqrt[3]{3}\!-\!\sqrt[3]{9}) } - \sqrt[3]{\!3 + 3(3\sqrt[3]{3}\!+\!\sqrt[3]{9})})}\right). \end{align*}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-ea0599823419e3e10d1b33e4770f908a_l3.png)
Numerical analysis approach to twin primes conjecture
Original research paper. Pages 175–183
Gabriele Di Pietro
Full paper (PDF, 194 Kb) | Abstract
The purpose of this paper is to demonstrate how the modified Sieve of Eratosthenes is used to have an approach to twin prime conjecture. If the Sieve is used in its basic form, it does not produce anything new. If it is used through the numerical analysis method explained in this paper, we obtain a specific counting of twin primes. This counting is based on the false assumption that distribution of primes follows punctually the Logarithmic Integral function denoted as Li(x) (see [5] and [10], pp. 174–176). It may be a starting point for future research based on this numerical analysis method technique that can be used in other mathematical branches.
Pauli–Fibonacci quaternions
Original research paper. Pages 184–193
Fügen Torunbalcı Aydın
Full paper (PDF, 177 Kb) | Abstract
The aim of this work is to consider the Pauli–Fibonacci quaternions and to present some properties involving this sequence, including the Binet’s formula and generating functions. Furthermore, the Honsberger identity, the generating function, d’Ocagne’s identity, Cassini’s identity, Catalan’s identity for these quaternions are given. The matrix representations for Pauli–Fibonacci quaternions are introduced.
Book review: “Arithmetic Functions”
Book review. Pages 194–195
Anthony Greville Shannon
Book review (PDF, 318 Kb)
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP2/26/2020.
Volume 27 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]()
![]() . This complements a 1996 result of Chung [2] which deals with the case
. This complements a 1996 result of Chung [2] which deals with the case ![]() . The method used relies on the sum of two squares theorem in number theory.
. The method used relies on the sum of two squares theorem in number theory.![]()
![]() denotes the set of prime numbers.
denotes the set of prime numbers.![]()
![]() , then it has infinitely many positive integer solutions of the form
, then it has infinitely many positive integer solutions of the form ![]() , where
, where ![]() and
and ![]() ,
, ![]() .
.![]()
![]() . We also give all arithmetical functions
. We also give all arithmetical functions ![]() which satisfy the relation
which satisfy the relation![]()
![]() , where
, where ![]() denotes the set of all positive integers.
denotes the set of all positive integers.![Rendered by QuickLaTeX.com \begin{align*} &\sqrt[3]{\sin\left(\frac{\pi}{9}\right)} + \sqrt[3]{\sin\left(\frac{2\pi}{9}\right)} + \sqrt[3]{\sin\left(\frac{14\pi}{9}\right)} \\ & = \left(-\frac{\sqrt[18]{3}}{2}\right) \left(\sqrt[3]{6+3\left(\sqrt[3]{6-3\sqrt[3]{9}}+ \sqrt[3]{3-3\sqrt[3]{9}}\right)}\right), \end{align*}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-2cfc2e8bb6884536753c45ead504214c_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} &\sqrt[3]{\tan\left(\frac{\pi}{9}\right)} + \sqrt[3]{\tan\left(\frac{4\pi}{9}\right)} + \sqrt[3]{\tan\left(\frac{7\pi}{9}\right)} \\ & = \left(-\sqrt[18]{3}\right) \left(\sqrt[3]{-3\sqrt[3]{3}+6+3(\sqrt[3]{\!21 - 3(3\sqrt[3]{3}\!-\!\sqrt[3]{9}) } - \sqrt[3]{\!3 + 3(3\sqrt[3]{3}\!+\!\sqrt[3]{9})})}\right). \end{align*}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-ea0599823419e3e10d1b33e4770f908a_l3.png)


