Volume 27 
Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
On a class of quartic Diophantine equations
Original research paper. Pages 1–6
F. Izadi, M. Baghalaghdam and S. Kosari
Full paper (PDF, 177 Kb) | Abstract
In this paper, by using elliptic curves theory, we study the quartic Diophantine equation (DE)
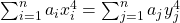
, where
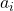
and
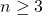
are fixed arbitrary integers. We try to transform this quartic to a cubic elliptic curve of positive rank. We solve the equation for some values of
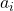
and
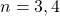
, and find infinitely many nontrivial solutions for each case in natural numbers, and show among other things, how some numbers can be written as sums of three, four, or more biquadrates in two different ways. While our method can be used for solving the equation for
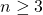
, this paper will be restricted to the examples where
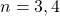
. Finally, we explain how to solve more general cases
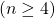
without giving concrete examples to case
.
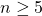
On the k-Mersenne–Lucas numbers
Original research paper. Pages 7–13
Mourad Chelgham and Ali Boussayoud
Full paper (PDF, 202 Kb) | Abstract
In this paper, we will introduce a new definition of
k-Mersenne–Lucas numbers and investigate some properties. Then, we obtain some identities and established connection formulas between
k-Mersenne–Lucas numbers and
k-Mersenne numbers through the use of Binet’s formula.
On Münchhausen numbers
Original research paper. Pages 14–21
Miroslav Kureš
Full paper (PDF, 266 Kb) | Abstract
The remarkable property of the number 3435, namely 3435 = 3
3 + 4
4 + 3
3 + 5
5, was formalized to the notion of Münchhausen numbers. Properties of these numbers are studied and it is showed that although there are only finitely many Münchhausen numbers in a given base
b, there are infinitely many Münchhausen numbers of the length 2 in all bases. A certain reversion in the definition gives the notion of so-called anti-Munchhausen numbers, search for them is computationally more effective.
On new arithmetic function relative to a fixed positive integer. Part 1
Original research paper. Pages 22–26
Brahim Mittou and Abdallah Derbal
Full paper (PDF, 154 Kb) | Abstract
The main purpose of this note is to define a new arithmetic function relative to a fixed positive integer and to study some of its properties.
Odd/even cube-full numbers
Original research paper. Pages 27–31
Tippawan Puttasontiphot and Teerapat Srichan
Full paper (PDF, 148 Kb) | Abstract
In this paper we use an elementary method to give an asymptotical ratio of odd to even cube-full numbers and show that it is asymptotically 1 : 1 + 2
−1/3 + 2
−2/3.
A study on some generalized multiplicative and generalized additive arithmetic functions
Original research paper. Pages 32–44
D. Bhattacharjee
Full paper (PDF, 600 Kb) | Abstract
In this paper by an arithmetic function we shall mean a real-valued function on the set of positive integers. We recall the definitions of some common arithmetic convolutions. We also recall the definitions of a multiplicative function, a generalized multiplicative function (or briefly a
GM-function), an additive function and a generalized additive function (or briefly a
GA-function). We shall study in details some properties of
GM-functions as well as
GA-functions using some particular arithmetic convolutions namely the Narkiewicz’s
A-product and the author’s
B-product. We conclude our discussion with some examples.
Bi-unitary multiperfect numbers, IV(b)
Original research paper. Pages 45–69
Pentti Haukkanen and Varanasi Sitaramaiah
Full paper (PDF, 297 Kb) | Abstract
On a Diophantine equation arising in the history of mathematics
Original research paper. Pages 70–75
József Sándor and Krassimir Atanassov
Full paper (PDF, 136 Kb) | Abstract
In the present paper, we offer the complete solution to a Diophantine equation, considered by S. Naranan [2]. For the history of the problem, see also L. E. Dickson [1].
Finiteness of lattice points on varieties F(y) = F(g(𝕏)) + r(𝕏) over imaginary quadratic fields
Original research paper. Pages 76–90
Lukasz Nizio
Full paper (PDF, 283 Kb) | Abstract
We construct affine varieties over
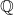
and imaginary quadratic number fields
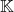
with a finite number of
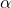
-lattice points for a fixed
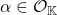
, where
denotes the ring of algebraic integers of
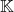
. These varieties arise from equations of the form
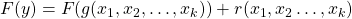
, where
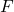
is a rational function,
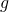
and
are polynomials over
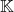
, and the degree of
is relatively small. We also give an example of an affine variety of dimension two, with a finite number of algebraic integral points. This variety is defined over the cyclotomic field
.
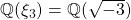
A note on Q-matrices and higher order Fibonacci polynomials
Original research paper. Pages 91–100
Paolo Emilio Ricci
Full paper (PDF, 219 Kb) | Abstract
The results described in a recent article, relative to a representation formula for the generalized Fibonacci sequences in terms of
Q-matrices are extended to the case of Fibonacci, Tribonacci and R-bonacci polynomials.
The Oresme sequence: The generalization of its matrix form and its hybridization process
Original research paper. Pages 101–111
Milena Carolina dos Santos Mangueira, Renata Passos Machado Vieira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 230 Kb) | Abstract
This article deals with the generalization of the matrix form of the Oresme sequence, extending it to the field of integers. In addition, the two valid generating matrices were discussed, through the permutation of the rows and columns, respectively, totaling two valid matrices of Oresme for the left-hand side, and two more generating matrices of Oresme for the right-hand side. In addition, a new Oresme sequence was introduced, given through the hybridization process of these numbers, obtaining mathematical properties and theorems, inherent to this process.
The character sum of polynomials with k variables and two-term exponential sums
Original research paper. Pages 112–124
Xu Xiaoling, Zhang Jiafan and Zhang Wenpeng
Full paper (PDF, 201 Kb) | Abstract
The main purpose of this paper is using the properties of the classical Gauss sums and the analytic methods to study the computational problem of one kind of hybrid power mean involving the character sums of polynomials with k variables and the two-term exponential sums, and give an identity and asymptotic formula for it.
A very general binomial matrix
Original research paper. Pages 125–133
Leo Betthauser, Ömür Deveci and Josh Hiller
Full paper (PDF, 181 Kb) | Abstract
We define the very general binomial matrix and find its eigendecomposition over arbitrary rings when such a decomposition is possible. Using this decomposition, we are able to compute the order of several varieties of Pascal’s matrices.
How to sum powers of balancing numbers efficiently
Original research paper. Pages 134–137
Helmut Prodinger
Full paper (PDF, 145 Kb) | Abstract
Balancing numbers possess, as Fibonacci numbers, a Binet formula. Using this, partial sums of arbitrary powers of balancing numbers can be summed explicitly. For this, as a first step, a power
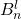
is expressed as a linear combination of
.
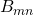
Characterization of ideals of rhotrices over a ring and its applications
Original research paper. Pages 138–147
Kailash M. Patil
Full paper (PDF, 236 Kb) | Abstract
We define higher order rhotrices over a commutative unital ring
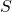
and obtain a ring
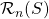
of rhotrices of the order
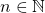
. We characterize the ideals and maximal ideals of
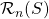
. As a particular case, we record ideals of rhotrix rings over integers and rhotrix algebras over complex plane
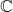
. As an application, we characterize the maximal ideals of the commutative unital Banach algebra
.
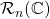
On the connections between Pell numbers and Fibonacci p-numbers
Original research paper. Pages 148–160
Anthony G. Shannon, Özgür Erdağ and Ömür Deveci
Full paper (PDF, 235 Kb) | Abstract
In this paper, we define the Fibonacci–Pell
p-sequence and then we discuss the connection of the Fibonacci–Pell
p-sequence with the Pell and Fibonacci
p-sequences. Also, we provide a new Binet formula and a new combinatorial representation of the Fibonacci–Pell
p-numbers by the aid of the
n-th power of the generating matrix of the Fibonacci–Pell
p-sequence. Furthermore, we derive relationships between the Fibonacci–Pell
p-numbers and their permanent, determinant and sums of certain matrices.
A note on Mersenne Padovan and Perrin numbers
Original research paper. Pages 161–170
Bir Kafle, Salah Eddine Rihane and Alain Togbé
Full paper (PDF, 215 Kb) | Abstract
In this paper, we determine all the Mersenne numbers which are in the sequences of Padovan and Perrin numbers, respectively.
Pell–Padovan generalized quaternions
Original research paper. Pages 171–187
Zehra İşbilir and Nurten Gürses
Full paper (PDF, 247 Kb) | Abstract
The aim of this article is to introduce Pell–Padovan generalized quaternions. It also derives new properties associated with these and takes into account negative indices. Additionally, it presents generating function, Binet-like formula, Simson formula, matrix representations, and several summation properties.
Triple sums including Fibonacci numbers with three binomial coefficients
Original research paper. Pages 188–197
Funda Taşdemir
Full paper (PDF, 179 Kb) | Abstract
In this paper, we consider some triple sums that involve Fibonacci numbers with three binomial coefficients. We chose the indices of Fibonacci numbers as linear combination of the summation indices. Moreover, various types of alternating analogues of them whose powers depend on the index or indices are computed. These sums are evaluated in nice multiplication forms in terms of Fibonacci and Lucas numbers.
Catalan transform of the k-Pell, k-Pell–Lucas and modified k-Pell sequence
Original research paper. Pages 198–207
Merve Taştan and Engin Özkan
Full paper (PDF, 865 Kb) | Abstract
In this study, we present the Catalan transforms of the
k-Pell sequence, the
k-Pell–Lucas sequence and the Modified
k-Pell sequence and examine the properties of the sequences. Then we apply the Hankel transform to the Catalan transforms of the
k-Pell sequence, the Catalan transform of the
k-Pell–Lucas sequence and the Catalan transform of the Modified
k-Pell sequence. Also, we obtain the generating functions of the Catalan transform of the
k-Pell sequence,
k-Pell–Lucas sequence and Modified
k-Pell sequence. Furthermore, we acquire an interesting characteristic related to the determinant of the Hankel transform of the sequences.
On the spectra of a new duplication based corona of graphs
Original research paper. Pages 208–220
Renny P. Varghese and D. Susha
Full paper (PDF, 201 Kb) | Abstract
In this paper we introduce a new corona-type product of graphs namely
duplication corresponding corona. Here we mainly determine the adjacency, Laplacian and signless Laplacian spectra of the new graph product. In addition to that, we find out the incidence energy, the number of spanning trees, Kirchhoff index and Laplacian-energy-like invariant of the new graph. Also we discuss some new classes of cospectral graphs.
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP2/26/2020.
Volume 27 Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
of a positive integer 
is called a unitary divisor if 
and 
is unity. The concept of a bi-unitary divisor is due to D. Surynarayana (1972). Let 
denote the sum of the bi-unitary divisors of 
for some 
. For 
we obtain the bi-unitary triperfect numbers.
, where 
and 
is odd. In part IV(a) we solved partly the case 
. We proved that if 
, where 
, then 
. We then solved completely the case 
. In the present paper we give some partial results concerning the case 
under the assumption 
