Volume 27 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Relations between Rα, Rβ and Rm functions related to Jacobi’s triple-product identity and the family of theta-function identities
Original research paper. Pages 1–11
M. P. Chaudhary
Full paper (PDF, 201 Kb) | Abstract
In this paper, the author establishes a set of three new theta-function identities involving Rα, Rβ and Rm functions which are based upon a number of q-product identities and Jacobi’s celebrated triple-product identity. These theta-function identities depict the inter-relationships that exist among theta-function identities and combinatorial partition-theoretic identities. Here, in this paper we answer a open question of Srivastava et al [33], and established relations in terms of Rα, Rβ and Rm (for m = 1, 2, 3), and q-products identities. Finally, we choose to further emphasize upon some close connections with combinatorial partition-theoretic identities.
The abundancy index of divisors of odd perfect numbers – Part II
Original research paper. Pages 12–19
Keneth Adrian Precillas Dagal and Jose Arnaldo Bebita Dris
Full paper (PDF, 198 Kb) | Abstract
In this note, we show that if N = qkn2 is an odd perfect number with special prime q, and N is not divisible by 3, then the inequality q < n holds. We then give another unconditional proof for the inequality q < n which is independent of the results of Brown and Starni.
Bi-unitary multiperfect numbers, V
Original research paper. Pages 20–40
Pentti Haukkanen and Varanasi Sitaramaiah
Full paper (PDF, 261 Kb) | Abstract
A divisor
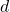
of a positive integer

is called a unitary divisor if
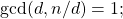
and
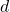
is called a bi-unitary divisor of

if the greatest common unitary divisor of
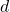
and
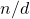
is unity. The concept of a bi-unitary divisor is due to D. Surynarayana (1972).
Let
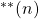
denote the sum of the bi-unitary divisors of

. A positive integer

is called a bi-unitary multiperfect number if
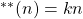
for some
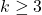
. For
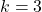
we obtain the bi-unitary triperfect numbers.
Peter Hagis (1987) proved that there are no odd bi-unitary multiperfect numbers. The present paper is part V in a series of papers on even bi-unitary multiperfect numbers. In parts I, II and III we determined all bi-unitary triperfect numbers of the form 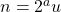 , where
, where 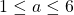 and
and 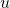 is odd. In parts IV(a-b) we solved partly the case
is odd. In parts IV(a-b) we solved partly the case 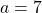 . In this paper we fix the case
. In this paper we fix the case 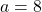 . In fact, we show that
. In fact, we show that 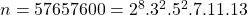 is the only bi-unitary triperfect number of the present type.
is the only bi-unitary triperfect number of the present type.
Inequalities for generalized divisor functions
Original research paper. Pages 41–48
József Sándor
Full paper (PDF, 218 Kb) | Abstract
We offer inequalities to
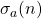
as a function of the real variable

: Monotonicity and convexity properties to this and related functions are proved, too. Extensions and improvements of known results are provided.
On two theorems of Vassilev-Missana
Original research paper. Pages 49–50
Richard P. Brent
Full paper (PDF, 134 Kb) | Abstract
We show that Theorem 1 of Vassilev-Missana [this journal, 2016, 22(4), 12–15] is false, and deduce that Theorem 2 of the same paper is also false.
A note on prime zeta function and Riemann zeta function. Corrigendum
Original research paper. Pages 51–53
Mladen Vassilev-Missana
Full paper (PDF, 141 Kb) | Abstract
In [1] the author proposed two new results concerning the prime zeta function and the Riemann zeta function but they turn out to be wrong. In the present paper we provide their correct form.
Partial sum of the products of the Horadam numbers with subscripts in arithmetic progression
Original research paper. Pages 54–63
Kunle Adegoke, Robert Frontczak and Taras Goy
Full paper (PDF, 187 Kb) | Abstract
We evaluate the partial sum of the products of the terms of any two Horadam sequences with subscripts in arithmetic progression. Illustrative examples are drawn from six well-known Horadam sequences.
A formula for the number of non-negative integer solutions of a1x1 + a2x2 + ··· + amxm = n in terms of the partial Bell polynomials
Original research paper. Pages 64–69
Sumit Kumar Jha
Full paper (PDF, 187 Kb) | Abstract
We derive a formula for the number of non-negative integer solutions of the equation

in terms of the partial Bell polynomials via the Faa di Bruno’s formula.
Perrin’s bivariate and complex polynomials
Original research paper. Pages 70–78
Renata Passos Machado Vieira, Milena Carolina dos Santos Mangueira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 223 Kb) | Abstract
In this article, a study is carried out around the Perrin sequence, these numbers marked by their applicability and similarity with Padovan’s numbers. With that, we will present the recurrence for Perrin’s polynomials and also the definition of Perrin’s complex bivariate polynomials. From this, the recurrence of these numbers, their generating function, generating matrix and Binet formula are defined.
Regular polygons, Morgan-Voyce polynomials, and Chebyshev polynomials
Original research paper. Pages 79–87
Jorma K. Merikoski
Full paper (PDF, 196 Kb) | Abstract
We say that a monic polynomial with integer coefficients is a polygomial if its each zero is obtained by squaring the edge or a diagonal of a regular n-gon with unit circumradius. We find connections of certain polygomials with Morgan-Voyce polynomials and further with Chebyshev polynomials of second kind.
On the Diophantine equations z2 = f(x)2 ± f(x)f(y) + f(y)2
Original research paper. Pages 88–100
Qiongzhi Tang
Full paper (PDF, 251 Kb) | Abstract
Using the theory of Pell equation, we study the non-trivial positive integer solutions of the Diophantine equations
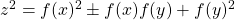
for certain polynomials
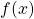
, which mean to construct integral triangles with two sides given by the values of polynomials
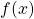
and
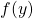
with the intersection angle
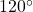
or
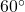
.
Sums of powers of integers and hyperharmonic numbers
Original research paper. Pages 101–110
José Luis Cereceda
Full paper (PDF, 191 Kb) | Abstract
In this paper, we obtain a new formula for the sums of k-th powers of the first n positive integers, Sk(n), that involves the hyperharmonic numbers and the Stirling numbers of the second kind. Then, using an explicit representation for the hyperharmonic numbers, we generalize this formula to the sums of powers of an arbitrary arithmetic progression. Furthermore, we express the Bernoulli polynomials in terms of hyperharmonic polynomials and Stirling numbers of the second kind. Finally, we extend the obtained formula for Sk(n) to negative values of n.
On the connections among Fibonacci, Pell, Jacobsthal and Padovan numbers
Original research paper. Pages 111–128
Ömür Deveci
Full paper (PDF, 248 Kb) | Abstract
In this paper, we define the Fibonacci–Jacobsthal, Padovan–Fibonacci, Pell–Fibonacci, Pell–Jacobsthal, Padovan–Pell and Padovan–Jacobsthal sequences which are directly related with the Fibonacci, Jacobsthal, Pell and Padovan numbers and give their structural properties by matrix methods. Then we obtain new relationships between Fibonacci, Jacobsthal, Pell and Padovan numbers.
Generalized Lucas numbers of the form 3 × 2m
Original research paper. Pages 129–136
Salah Eddine Rihane, Chefiath Awero Adegbindin and Alain Togbé
Full paper (PDF, 204 Kb) | Abstract
For an integer
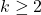
, let
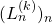
be the

-generalized Lucas sequence which starts with
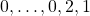
(

terms) and each term afterwards is the sum of the

preceding terms. In this paper, we look the

-generalized Lucas numbers of the form
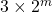
i.e. we study the Diophantine equation
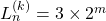
in positive integers
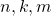
with
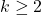
.
Some identities of generalized Tribonacci and Jacobsthal polynomials
Original research paper. Pages 137–147
Abdeldjabar Hamdi and Salim Badidja
Full paper (PDF, 212 Kb) | Abstract
In this study, we denote
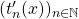
the generalized Tribonacci polynomials, which are defined by
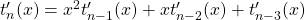
,
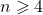
, with
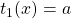
,
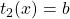
,
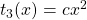
and we drive an explicit formula of
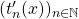
in terms of their coefficients
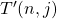
, Also, we establish some properties of
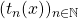
. Similarly, we study the Jacobsthal polynomials
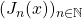
, where
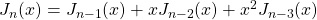
,
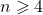
, with
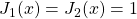
,
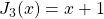
and describe some properties.
The generalized k-Fibonacci polynomials and generalized k-Lucas polynomials
Original research paper. Pages 148–158
Merve Taştan, Engin Özkan and Anthony G. Shannon
Full paper (PDF, 802 Kb) | Abstract
In this paper, we define new families of Generalized Fibonacci polynomials and Generalized Lucas polynomials and develop some elegant properties of these families. We also find the relationships between the family of the generalized k-Fibonacci polynomials and the known generalized Fibonacci polynomials. Furthermore, we find new generalizations of these families and the polynomials in matrix representation. Then we establish Cassini’s Identities for the families and their polynomials. Finally, we suggest avenues for further research.
More identities on Fibonacci and Lucas hybrid numbers
Original research paper. Pages 159–167
Nazmiye Yilmaz
Full paper (PDF, 159 Kb) | Abstract
We give several identities about Fibonacci and Lucas hybrid numbers. We introduce the Fibonacci and Lucas hybrid numbers with negative subscripts. We obtain different Cassini identities for the conjugate of the Fibonacci and Lucas hybrid numbers by two different determinant definitions of a hybrid square matrix (whose entries are hybrid numbers).
A short remark on a new Fibonacci-type sequence
Original research paper. Pages 168–171
Krassimir T. Atanassov
Full paper (PDF, 124 Kb) | Abstract
A new Fibonacci-type sequence is constructed and for it is proved that it has a basis with 24 elements.
Classifying Galois groups of an orthogonal family of quartic polynomials
Original research paper. Pages 172–190
Pradipto Banerjee and Ranjan Bera
Full paper (PDF, 159 Kb) | Abstract
We consider the quartic generalized Laguerre polynomials
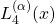
for
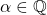
. It is shown that except
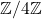
, every transitive subgroup of
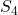
appears as the Galois group of
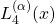
for infinitely many
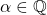
. A precise characterization of
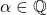
is obtained for each of these occurrences. Our methods involve the standard use of resolvent cubics and the theory of

-adic Newton polygons. Using these, the Galois group computations are reduced to Diophantine problem of finding integer and rational points on certain curves.
On r-dynamic coloring of comb graphs
Original research paper. Pages 191–200
K. Kalaiselvi, N. Mohanapriya and J. Vernold Vivin
Full paper (PDF, 185 Kb) | Abstract
An

-dynamic coloring of a graph

is a proper coloring of

such that every vertex in
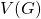
has neighbors in at least
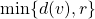
different color classes. The

-dynamic chromatic number of graph

denoted as
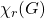
, is the least

such that

has a coloring. In this paper we obtain the

-dynamic chromatic number of the central graph, middle graph, total graph, line graph, para-line graph and sub-division graph of the comb graph

denoted by
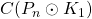
,
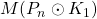
,
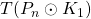
,
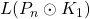
,
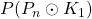
and
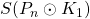
respectively by finding the upper bound and lower bound for the

-dynamic chromatic number of the Comb graph.
Refined enumeration of 2-noncrossing trees
Original research paper. Pages 201–210
Isaac Owino Okoth
Full paper (PDF, 197 Kb) | Abstract
A 2-noncrossing tree is a connected graph without cycles that can be drawn in the plane with its vertices on the boundary of circle such that the edges are straight line segments that do not cross and all the vertices are coloured black and white with no ascent (i, j), where i and j are black vertices, in a path from the root. In this paper, we use generating functions to prove a formula that counts 2-noncrossing trees with a black root to take into account the number of white vertices of indegree greater than zero and black vertices. Here, the edges of the 2-noncrossing trees are oriented from a vertex of lower label towards a vertex of higher label. The formula is a refinement of the formula for the number of 2-noncrossing trees that was obtained by Yan and Liu and later on generalized by Pang and Lv. As a consequence of the refinement, we find an equivalent refinement for 2-noncrossing trees with a white root, among other results.
Book presentation: “Arithmetic Functions”
Book presentation. Pages 211–212
Book presentation (PDF, 324 Kb)
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP2/26/2020.
Volume 27 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() , where
, where ![]() and
and ![]() is odd. In parts IV(a-b) we solved partly the case
is odd. In parts IV(a-b) we solved partly the case ![]() . In this paper we fix the case
. In this paper we fix the case ![]() . In fact, we show that
. In fact, we show that ![]() is the only bi-unitary triperfect number of the present type.
is the only bi-unitary triperfect number of the present type.

