Sums of powers of integers and hyperharmonic numbers

José Luis Cereceda
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 27, 2021, Number 2, Pages 101–110
DOI: 10.7546/nntdm.2021.27.2.101-110
Full paper (PDF, 191 Kb)

Details

Authors and affiliations

José Luis Cereceda
Collado Villalba, 28400 Madrid, Spain

Abstract

In this paper, we obtain a new formula for the sums of -th powers of the first positive integers, , that involves the hyperharmonic numbers and the Stirling numbers of the second kind. Then, using an explicit representation for the hyperharmonic numbers, we generalize this formula to the sums of powers of an arbitrary arithmetic progression. Furthermore, we express the Bernoulli polynomials in terms of hyperharmonic polynomials and Stirling numbers of the second kind. Finally, we extend the obtained formula for to negative values of .

Keywords

• Sums of powers of integers
• Hyperharmonic numbers
• Stirling numbers of the second kind
• Bernoulli polynomials
• Hyperharmonic polynomials

2020 Mathematics Subject Classification

• 11B68
• 11B25
• 11B83

References

1. Apostol, T. M. (2008). A primer on Bernoulli numbers and polynomials. Mathematics Magazine, 81(3), 178–190.
2. Benjamin, A. T., Gaebler, D., & Gaebler, R. (2003). A combinatorial approach to
   hyperharmonic numbers. Integers, 3, 1–9. Article #A15.
3. Boyadzhiev, K. N. (2018). Notes on the Binomial Transform: Theory and Table with Appendix on Stirling Transform. World Scientific. Singapore.
4. Cereceda, J. L. (2015). An introduction to hyperharmonic numbers. International Journal of Mathematical Education in Science and Technology, 46(3), 461–469.
5. Cheon, Gi.-S., & El-Mikkawy, M. E. A. (2008). Generalized harmonic numbers with Riordan arrays. Journal of Number Theory, 128(2), 413–425.
6. Conway, J. H., & Guy, R. K. (1996). The Book of Numbers. Copernicus. New York.
7. Dil, A., & Mező, I. (2008). A symmetric algorithm for hyperharmonic and Fibonacci numbers. Applied Mathematics and Computation, 206(2), 942–951.
8. Dil, A. (2019). On the hyperharmonic function. Süleyman Demirel University, Journal of Natural and Applied Sciences, 23, Special Issue, 187–193.
9. Dil, A., & Muniroglu, E. (2020). Applications of derivative and difference operators on some sequences. Applicable Analysis and Discrete Mathematics, 14(2), 406–430.
10. Gould, H. W. (1972). Combinatorial Identities: A Standardized Set of Tables Listing 500 Binomial Coefficient Summations. Morgantown Printing and Binding Co., Morgantown (WV).
11. Gould, H. W. (1978). Evaluation of sums of convolved powers using Stirling and Eulerian numbers. The Fibonacci Quarterly, 16(6), 488–497.
12. Griffiths, M. (2002). Sums of powers of the terms in any finite arithmetic progression. Mathematical Gazette, 86(506), 269–271.
13. Jha, S. K. (2020). Two new explicit formulas for the Bernoulli numbers. Integers, 20, Article #A21, 5 pp.
14. Levy, L. S. (1970). Summation of the series 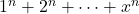using elementary calculus. American Mathematical Monthly, 77(8), 840–847.
15. Mező, I. (2009). Analytic extension of hyperharmonic numbers. Online Journal of Analytic Combinatorics, 4, Article 1, 9 pp.
16. Mező, I. (2020). Combinatorics and Number Theory of Counting Sequences. CRC Press. Taylor & Francis Group. Boca Raton (FL).
17. Newsome, N. J., Nogin, M. S., & Sabuwala, A. H. (2017). A proof of symmetry of the power sum polynomials using a novel Bernoulli number identity. Journal of Integer Sequences, 20, Article 17.6.6, 10 pp.
18. Owens, R. W. (1992). Sums of powers of integers. Mathematics Magazine, 65(1), 38–40.
19. Paule, P., & Schneider, C. (2003). Computer proofs of a new family of harmonic number identities. Advances in Applied Mathematics, 31(2), 359–378.
20. Qi, F., & Guo, B.-N. (2014). Alternative proofs of a formula for Bernoulli numbers in terms of Stirling numbers. Analysis, 34(3), 311–317.
21. Sherwood, H. (1970). Sums of powers of integers and Bernoulli numbers. Mathematical Gazette, 54(389), 272–274.
22. Sprugnoli, R. (1994). Riordan arrays and combinatorial sums. Discrete Mathematics, 132(1–3), 267–290.
23. Wu, D. W. (2001). Bernoulli numbers and sums of powers. International Journal of Mathematical Education in Science and Technology, 32(3), 440–443.