Volume 27, 2021, Number 4

Volume 27 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

A parametric family of quartic Thue inequalities
Original research paper. Pages 1–14
Salah Eddine Rihane, Mohand Ouamar Hernane and Alain Togbé
Full paper (PDF, 249 Kb) | Abstract

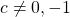
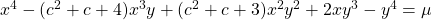
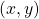
Let $c\neq 0,-1$ be an integer. In this paper, we use the method of Tzanakis to transform the quartic Thue equation $x^4 -(c^2+c+4) x^3y +(c^2+c+3) x^2 y^2 +2 xy^3 -y^4 = \mu$ into systems of Pell equations. Then, we determine all primitive solutions $(x,y)$ with $0<|\mu|\leq |c+1|$ .

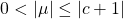
On Robin’s criterion for the Riemann Hypothesis
Original research paper. Pages 15–24
Safia Aoudjit, Djamel Berkane and Pierre Dusart
Full paper (PDF, 268 Kb) | Abstract

Robin’s criterion says that the Riemann Hypothesis is equivalent to

$\forall n\geq 5041, \ \ \frac{\sigma(n)}{n}\leq e^{\gamma}\log_2 n,$

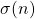where $\sigma(n)$ is the sum of the divisors of 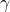$n$ , $\gamma$ represents the Euler–Mascheroni constant, and 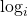$\log_i$ denotes the 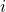$i$ -fold iterated logarithm. In this note we get the following better effective estimates:

$\begin{equation*} \forall n\geq3, \ \frac{\sigma(n)}{n}\leq e^{\gamma}\log_2 n+\frac{0.3741}{\log_2^2n}. \end{equation*}$

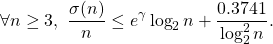
The idea employed will lead us to a possible new reformulation of the Riemann Hypothesis in terms of arithmetic functions.

New consequences of prime-counting function
Original research paper. Pages 25–31
Sadani Idir
Full paper (PDF, 204 Kb) | Abstract

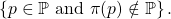
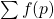
Our objective in this paper is to study a particular set of prime numbers, namely $\left\{p\in\mathbb{P} \ \text{and} \ \pi(p)\notin\mathbb{P}\right\}.$ As a consequence, estimations of the form $\sum{f(p)}$ with $p$ being prime belonging to this set are derived.

Leonardo’s three-dimensional relations and some identities
Original research paper. Pages 32–42
Renata Passos Machado Vieira, Milena Carolina dos Santos Mangueira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 181 Kb) | Abstract

In this work, new results are explored in relation to the Leonardo sequence. With that, a study about this second order recursive sequence, little explored in the mathematical scope, is briefly presented, relating it to the Fibonacci sequence. Thus, its complexification process is carried out, where from its one-dimensional model, imaginary units are inserted, obtaining Leonardo’s three-dimensional numbers. In this way, the imaginary units i and j are inserted. Finally, some three-dimensional identities are presented for Leonardo’s numbers.

The congruence speed formula
Original research paper. Pages 43–61
Marco Ripà
Full paper (PDF, 227 Kb) | Abstract

We solve a few open problems related to a peculiar property of the integer tetration ^ba, which is the constancy of its congruence speed for any sufficiently large b = b(a). Assuming radix-10 (the well known decimal numeral system), we provide an explicit formula for the congruence speed V(a) ∈ ℕ₀ of any a ∈ ℕ − {0} that is not a multiple of 10. In particular, for any given n ∈ ℕ, we prove to be true Ripà’s conjecture on the smallest a such that V(a) = n. Moreover, for any a ≠ 1 ∶ a ≢ 0 (mod 10), we show the existence of infinitely many prime numbers, p_j = p_j(V(a)), such that V(p_j) = V(a).

An elementary unified approach to prove some identities involving Fibonacci and Lucas numbers
Original research paper. Pages 62–79
Moussa Benoumhani
Full paper (PDF, 236 Kb) | Abstract

Using the explicit formulas of the generating polynomials of Fibonacci and Lucas, we prove some new identities involving Fibonacci and Lucas numbers. As an application of these identities, we show how some Diophantine equations have infinitely many solutions. To illustrate the powerful of this elementary method, we give proofs of many known formulas.

Explicit formulas for Euler polynomials and Bernoulli numbers
Original research paper. Pages 80–89
Laala Khaldi, Farid Bencherif and Miloud Mihoubi
Full paper (PDF, 207 Kb) | Abstract

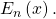
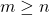
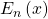
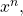
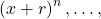
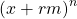
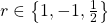
In this paper, we give several explicit formulas involving the $n$ -th Euler polynomial $E_{n}\left(x\right).$ For any fixed integer $m\geq n$ , the obtained formulas follow by proving that $E_{n}\left(x\right)$ can be written as a linear combination of the polynomials $x^{n},$ $\left(x+r\right)^{n},\ldots,$ $\left(x+rm\right)^{n}$ , with $r\in \left \{1,-1,\frac{1}{2}\right\}$ . As consequence, some explicit formulas for Bernoulli numbers may be deduced.

A simple proof of Linas’s theorem on Riemann zeta function
Original research paper. Pages 90–94
Jun Ikeda, Junsei Kochiya and Takato Ui
Full paper (PDF, 142 Kb) | Abstract

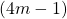
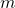
Linas Vepštas gives rapidly converging infinite representatives for values of Riemann zeta function at $\left(4m-1 \right)$ , where $m$ is a natural number. In this paper, we give a new simple proof. Also, we obtain two equation of values of Bernoulli numbers’ generating function by applying a corollary given in this paper.

Fibonacci-Zeta infinite series associated with the polygamma functions
Original research paper. Pages 95–103
Kunle Adegoke and Sourangshu Ghosh
Full paper (PDF, 172 Kb) | Abstract

We derive new infinite series involving Fibonacci numbers and Riemann zeta numbers. The calculations are facilitated by evaluating linear combinations of polygamma functions of the same order at certain arguments.

Series expansion of the Gamma function and its reciprocal
Original research paper. Pages 104–115
Ioana Petkova
Full paper (PDF, 284 Kb) | Abstract

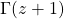
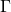
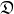
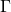
In this paper we give representations for the coefficients of the Maclaurin series for $\Gamma(z+1)$ and its reciprocal (where $\Gamma$ is Euler’s Gamma function) with the help of a differential operator $\mathfrak{D}$ , the exponential function and a linear functional $^{*}$ (in Theorem 3.1). As a result we obtain the following representations for $\Gamma$ (in Theorem 3.2):

$\begin{align*} \Gamma(z+1) & = \big(e^{-u(x)}e^{-z\mathfrak{D}}[e^{u(x)}]\big)^{*}, \\ \big(\Gamma(z+1)\big)^{-1} & = \big(e^{u(x)}e^{-z\mathfrak{D}}[e^{-u(x)}]\big)^{*}. \end{align*}$

Theorem 3.1 and Theorem 3.2 are our main results. With the help of the first theorem we give our approach for finding the coefficients of Maclaurin series for 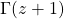$\Gamma(z+1)$ and its reciprocal in an explicit form.

Determinantal representations for the number of subsequences without isolated odd terms
Original research paper. Pages 116–121
Milica Anđelic and Carlos M. da Fonseca
Full paper (PDF, 157 Kb) | Abstract

In this short note we propose two determinantal representations for the number of subsequences without isolated odd terms are presented. One is based on a tridiagonal matrix and other on a Hessenberg matrix. We also establish a new explicit formula for the terms of this sequence based on Chebyshev polynomials of the second kind.

Binomial formulas via divisors of numbers
Original research paper. Pages 122–128
Karol Gryszka
Full paper (PDF, 193 Kb) | Abstract

The purpose of this note is to prove several binomial-like formulas whose exponents are values of the function ω(n) counting distinct prime factors of n.

Formulas for the n-th prime number
Original research paper. Pages 129–139
Krassimir T. Atanassov
Full paper (PDF, 205 Kb) | Abstract

A short review of formulas for the n-th prime number is given and some new formulas are introduced.

Algorithms for computing sums of powers of arithmetic progressions by using Eulerian numbers
Original research paper. Pages 140–148
Peter J. Shiue, Shen C. Huang and Jorge E. Reyes
Full paper (PDF, 286 Kb) | Abstract

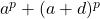
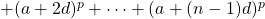
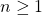
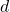
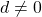
The sums of powers of arithmetic progressions is of the form $a^p+(a+d)^p$ $+(a+2d)^p+\cdots+(a+(n-1)d)^p$ , where $n\geq 1$ , $p$ is a non-negative integer, and $a$ and $d$ are complex numbers with $d\neq 0$ . This sum can be computed using classical Eulerian numbers [11] and general Eulerian numbers [12]. This paper gives a new method using classical Eulerian numbers to compute this sum. The existing formula that uses general Eulerian numbers are more algorithmically complex due to more numbers to compute. This paper presents and focuses on two novel algorithms involving both types of Eulerian numbers. This paper gives a comparison to Xiong et al.‘s result with general Eulerian numbers [12]. Moreover, an analysis of theoretical time complexities is presented to show our algorithm is less complex. Various values of $p$ are analyzed in the proposed algorithms to add significance to the results. 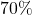The experimental results show the proposed algorithm remains around $70\%$ faster as $p$ increases.

On certain inequalities for the prime counting function
Original research paper. Pages 149–153
József Sándor
Full paper (PDF, 148 Kb) | Abstract

We study certain inequalities for the prime counting function π(x). Particularly, a new proof and a refinement of an inequality from [1] is provided.

A plane trigonometric proof for the case n = 4 of Fermat’s Last Theorem
Original research paper. Pages 154–163
Giri Prabhakar
Full paper (PDF, 221 Kb) | Abstract

We present a plane trigonometric proof for the case n = 4 of Fermat’s Last Theorem. We first show that every triplet of positive real numbers (a, b, c) satisfying a⁴ + b⁴ = c⁴ forms the sides of an acute triangle. The subsequent proof is founded upon the observation that the Pythagorean description of every such triangle expressed through the law of cosines must exactly equal the description of the triangle from the Fermat equation. On the basis of a geometric construction motivated by this observation, we derive a class of polynomials, the roots of which are the sides of these triangles. We show that the polynomials for a given triangle cannot all have rational roots. To the best of our knowledge, the approach offers new geometric and algebraic insight into the irrationality of the roots.

A note on the Neyman–Rayner triangle
Original research paper. Pages 164–166
A. G. Shannon
Full paper (PDF, 72 Kb) | Abstract

This note raises questions for other number theorists to tackle. It considers a triangle arising from some statistical research of John Rayner and his use of some orthonormal polynomials related to the Legendre polynomials. These are expressed in a way that challenges the generalizing them. In particular, the coefficients are expressed in a triangle and related to known sequences in the Online Encyclopedia of Integer Sequences. The note actually raises more questions than it answers when it links with the cluster algebra of Fomin and Zelevinsky.

Relations on higher dimensional Padovan sequences
Original research paper. Pages 167–179
Renata Passos Machado Vieira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 187 Kb) | Abstract

Many papers developed so far for Padovan sequences properties and its extensions usually follow the one-dimensional approach. The presented work introduces new relations for a higher dimensional sequence, this approach is adopted for two, three and n-dimensional Padovan Sequence. Several mathematical properties are discussed for the first time in the present work.

A few remarks on the values of the Bernoulli polynomials at rational arguments and some relations with ζ(2k + 1)
Original research paper. Pages 180–186
André Pierro de Camargo and Giulliano Cogui de Oliveira Teruya
Full paper (PDF, 216 Kb) | Abstract

A problem posed by Lehmer in 1938 asks for simple closed formulae for the values of the even Bernoulli polynomials at rational arguments in terms of the Bernoulli numbers. We discuss this problem based on the Fourier expansion of the Bernoulli polynomials. We also give some necessary and sufficient conditions for ζ(2k + 1) be a rational multiple of π^2k+1.

On k-circulant matrices with the generalized third-order Pell numbers
Original research paper. Pages 187–206
Yüksel Soykan
Full paper (PDF, 265 Kb) | Abstract

In this paper, we obtain explicit forms of the sum of entries, the maximum column sum matrix norm, the maximum row sum matrix norm, Euclidean norm, eigenvalues and determinant of k-circulant matrix with the generalized third-order Pell numbers. We also study the spectral norm of this k-circulant matrix. Furthermore, some numerical results for demonstrating the validity of the hypotheses of our results are given.

Factorizations of some lower triangular matrices and related combinatorial identities
Original research paper. Pages 207–218
Cahit Köme
Full paper (PDF, 264 Kb) | Abstract

In this study, we investigate the connection between second order recurrence matrix and several combinatorial matrices such as generalized r-eliminated Pascal matrix, Stirling matrix of the first and of the second kind matrices. We give factorizations and inverse factorizations of these matrices by virtue of the second order recurrence matrix. Moreover, we derive several combinatorial identities which are more general results of some earlier works.

Fundamental properties of extended Horadam numbers
Original research paper. Pages 219–235
Gülsüm Yeliz Şentürk, Nurten Gürses and Salim Yüce
Full paper (PDF, 302 Kb) | Abstract

In this paper, the extended Horadam numbers are introduced by using dual-generalized complex, hyperbolic-generalized complex and complex-generalized complex numbers. Then, generating function, Binet’s formula, D’Ocagne’s, Catalan’s and Cassini’s identities are given. Moreover, special matrix representations of the extended Horadam numbers are investigated. In conclusion, the results and classification of the special cases are introduced.

On Fibonacci quaternion matrix
Original research paper. Pages 236–244
Serpil Halici and Ömür Deveci
Full paper (PDF, 205 Kb) | Abstract

In this study, we have defined Fibonacci quaternion matrix and investigated its powers. We have also derived some important and useful identities such as Cassini’s identity using this new matrix.

Incomplete generalized Vieta–Pell and Vieta–Pell–Lucas polynomials
Original research paper. Pages 245–256
Bahar Kuloğlu, Engin Özkan and Anthony G. Shannon
Full paper (PDF, 149 Kb) | Abstract

In this paper, we introduce the incomplete Vieta–Pell and Vieta–Pell–Lucas polynomials. We give some properties, the recurrence relations and the generating function of these polynomials with suggestions for further research.

On k-Fibonacci hybrid numbers and their matrix representations
Original research paper. Pages 257–266
Fügen Torunbalcı Aydın
Full paper (PDF, 203 Kb) | Abstract

In this paper, k-Fibonacci hybrid numbers are defined. Also, some algebraic properties of k-Fibonacci hybrid numbers such as Honsberger identity, Binet Formula, generating functions, d’Ocagne identity, Cassini and Catalan identities are investigated. In addition, we also give 2 × 2 and 4 × 4 representations of the k-Fibonacci hybrid numbers HF_k,n.

On the dimension of an Abelian group
Original research paper. Pages 267–275
Timo Tossavainen and Pentti Haukkanen
Full paper (PDF, 192 Kb) | Abstract

We introduce a measure of dimensionality of an Abelian group. Our definition of dimension is based on studying perpendicularity relations in an Abelian group. For G ≅ ℤⁿ, dimension and rank coincide but in general they are different. For example, we show that dimension is sensitive to the overall dimensional structure of a finite or finitely generated Abelian group, whereas rank ignores the torsion subgroup completely.

Corrigendum to “The Oresme sequence: The generalization of its matrix form and its hybridization process” [Notes on Number Theory and Discrete Mathematics, Vol. 27, 2021, No. 1, 101–111]
Corrigendum. Pages 276–279
Milena Carolina dos Santos Mangueira, Renata Passos Machado Vieira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Corrigendum (PDF, 140 Kb) | Abstract

The present Corrigendum contains a list of corrections applicable to the authors’ paper [1].

This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP2/26/2020.

Volume 27 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Latest Issue

Journal Contents