Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Congratulations to our Editorial Board Members Prof. Taekyun Kim, Dr. Mladen Vassilev-Missana and Prof. Krassimir Atanassov for their anniversaries in 2024!
Editorial. Pages 663–664
Vassia Atanassova
Editorial (PDF, 583 Kb)
Algorithms for representing positive odd integers as the sum of arithmetic progressions
Original research paper. Pages 665–680
Peter J.-S. Shiue, Anthony G. Shannon, Shen C. Huang, Michael R. Schwob, Rama Venkat
Full paper (PDF, 226 Kb) | Abstract
This paper delves into the historical and recent developments in this area of mathematical inquiry, tracing the evolution from Wheatstone’s representation of powers of an integer as sums of arithmetic progressions to extensions of Sylvester’s Theorem (Sylvester and Franklin, [14]). Sylvester’s Theorem, a result that determines the representability of positive integers as sums of consecutive integers, has been the foundation for numerous extensions, including the representation of integers as sums of specific arithmetic progressions and powers of such progressions. The recent works of Ho et al. [3] and Ho et al. [4] have further expanded on Sylvester’s Theorem, offering a procedural approach to compute the representability of positive integers in the context of arithmetic progressions. In this paper, efficient algorithms to compute the number of ways to represent an odd positive integer as sums of powers of arithmetic progressions are presented.
Quotients of sequences under the binomial convolution
Original research paper. Pages 681–690
Pentti Haukkanen
Full paper (PDF, 221 Kb) | Abstract
This paper gives expressions for the solution
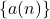
of the equation
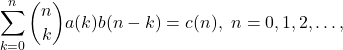
where 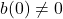 , that is, of the equation
, that is, of the equation 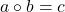 in
in  , where
, where  is the binomial convolution. These expressions are classified as recursive, explicit, determinant, exponential generating function and convolutional expressions. These expressions are compared with those under the usual Cauchy convolution. Several special cases and examples of combinatorial nature are also discussed.
is the binomial convolution. These expressions are classified as recursive, explicit, determinant, exponential generating function and convolutional expressions. These expressions are compared with those under the usual Cauchy convolution. Several special cases and examples of combinatorial nature are also discussed.
New congruences modulo powers of 2 for k-regular overpartition pairs
Original research paper. Pages 691–703
Riyajur Rahman and Nipen Saikia
Full paper (PDF, 230 Kb) | Abstract
Let
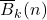
denote the number of

regular overpartition pairs where a

-regular overpartition pair of

is a pair of

-regular overpartitions
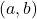
in which the sum of all the parts is

. Naika and Shivasankar (2017) proved infinite families of congruences for
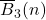
and
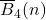
. In this paper, we prove infinite families of congruences modulo powers of
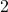
for
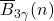
,
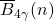
and
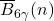
.
Revisiting some r-Fibonacci sequences and Hessenberg matrices
Original research paper. Pages 704–715
Carlos M. da Fonseca, Paulo Saraiva and Anthony G. Shannon
Full paper (PDF, 244 Kb) | Abstract
The relationship between different generalizations of Fibonacci numbers and matrices is common in the literature. However, the basic relation of such sequences with Hessenberg matrices is often not properly explored. In this work we revisit some classic results and present some applications in recent contexts.
Powers of the operator 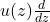 and their connection with some combinatorial numbers
and their connection with some combinatorial numbers
Original research paper. Pages 716–734
Ioana Petkova
Full paper (PDF, 322 Kb) | Abstract
In this paper the operator
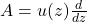
is considered, where
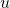
is an entire or meromorphic function in the complex plane. The expansion of
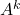
(
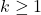
) with the help of the powers of the differential operator
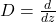
is obtained, and it is shown that this expansion depends on special numbers. Connections between these numbers and known combinatorial numbers are given. Some special cases of the operator
, corresponding to
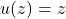
,
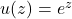
,
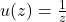
, are considered.
On (k,p)-Fibonacci numbers and matrices
Original research paper. Pages 735–744
Sinan Karakaya, Halim Özdemir and Tuğba Demirkol
Full paper (PDF, 253 Kb) | Abstract
In this paper, some relations between the powers of any matrices
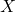
satisfying the equation
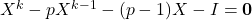
and
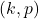
-Fibonacci numbers are established with
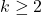
. First, a result is obtained to find the powers of the matrices satisfying the condition above via
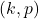
-Fibonacci numbers. Then, new properties related to
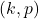
-Fibonacci numbers are given. Moreover, some relations between the sequence
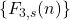
and the generalized Fibonacci sequence
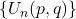
are also examined.
The complex-type Pell p-numbers
Original research paper. Pages 745–754
Yeşim Aküzüm, Hüseyin Aydın and Ömür Deveci
Full paper (PDF, 245 Kb) | Abstract
In this paper, we define the complex-type Pell p-numbers and give the generating matrix of these defined numbers. Then, we produce the combinatorial representation, the generating function, the exponential representation and the sums of the complex-type Pell p-numbers. Also, we derive the determinantal and the permanental representations of the complex-type Pell p-numbers by using certain matrices which are obtained from the generating matrix of these numbers. Finally, we obtain the Binet formula for the complex-type Pell p-number.
Partitions of numbers and the algebraic principle of Mersenne, Fermat and even perfect numbers
Original research paper. Pages 755–775
A. M. S. Ramasamy
Full paper (PDF, 305 Kb) | Abstract
Let ρ be an odd prime greater than or equal to 11. In a previous work, starting from an M-cycle in a finite field 𝔽ρ, it has been established how the divisors of Mersenne, Fermat and Lehmer numbers arise. The converse question has been taken up in a succeeding work and starting with a factor of these numbers, a method has been provided to find an odd prime ρ and the M-cycle in 𝔽ρ contributing the factor under consideration. Continuing the study of the two previous works, a certain type of partition of a natural number is considered in the present paper. Concerning the Mersenne, Fermat and even perfect numbers, the algebraic principle is established.
A note on Diophantine inequalities in function fields
Original research paper. Pages 776–786
Kathryn Wilson
Full paper (PDF, 249 Kb) | Abstract
We will discuss how the Bentkus–Götze–Freeman variant of the Davenport–Heilbronn circle method can be used to study
![Rendered by QuickLaTeX.com \mathbb{F}_q[t]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-0254ba6667c1bba60110336aa23aea97_l3.png)
solutions to inequalities of the form
![Rendered by QuickLaTeX.com \[\mathrm{ord}(\lambda_1p_1^k+\cdots+\lambda_sp_s^k-\gamma)<\tau , \]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-25ac13913a5d82377d9658e0464e873d_l3.png)
where constants 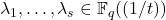 satisfy certain conditions. This result is a generalization of the work done by Spencer in [11] to count the number of solutions to inequalities of the form
satisfy certain conditions. This result is a generalization of the work done by Spencer in [11] to count the number of solutions to inequalities of the form
![Rendered by QuickLaTeX.com \[\mathrm{ord}(\lambda_1p_1^k+\cdots+\lambda_sp_s^k)<\tau.\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-9e07634d1a3cca800355a4ce7bb48562_l3.png)
Monophonic domination polynomial of the path graph
Original research paper. Pages 787–796
P. Arul Paul Sudhahar and W. Jebi
Full paper (PDF, 222 Kb) | Abstract
Let
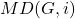
be the family of monophonic dominating sets of a graph

with cardinality
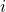
and let
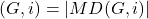
. Then the monophonic domination polynomial
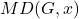
of

is defined as
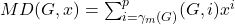
, where
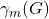
is the monophonic domination number of

. In this paper we have determined the family of monophonic dominating sets of the path graph
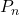
with cardinality
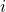
. Also, the monophonic domination polynomial of the path graph is calculated and some properties of the coefficient
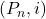
is discussed.
An analytical formula for Bell numbers
Original research paper. Pages 797–802
Vembu Ramachandran and Roopkumar Rajakumar
Full paper (PDF, 201 Kb) | Abstract
We present an analytic formula for Bell numbers through counting the number of uniform structures on a finite set.
Irrationality and transcendence of infinite series of rational terms
Original research paper. Pages 803–810
Lazhar Dhaouadi
Full paper (PDF, 209 Kb) | Abstract
The aim of this paper is to prove two results concerning the irrationality and transcendence of a certain class of infinite series which consist of rational numbers and converge very quickly.
Generalized Bronze Leonardo sequence
Original research paper. Pages 811–824
Engin Özkan and Hakan Akkuş
Full paper (PDF, 624 Kb) | Abstract
In this study, we define the Bronze Leonardo, Bronze Leonardo–Lucas, and Modified Bronze Leonardo sequences, and some terms of these sequences are given. Then, we give special summation formulas, special generating functions, etc. Also, we obtain the Binet formulas in three different ways. The first is in the known classical way, the second is with the help of the sequence’s generating functions, and the third is with the help of the matrices. In addition, we find the special relations between the terms of the Bronze Leonardo, Bronze Leonardo–Lucas, and Modified Bronze Leonardo sequences. Moreover, we examine the relationships among the Bronze Fibonacci and Bronze Lucas sequences of these sequences. Finally, we associate these sequences with the matrices.
A note on the Diophantine equation 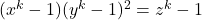
Original research paper. Pages 825–831
Yangcheng Li
Full paper (PDF, 223 Kb) | Abstract
We prove that, for

, the Diophantine equation
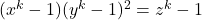
in positive integers
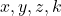
with
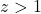
, has no solutions satisfying
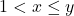
or
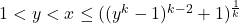
.
Moments and asymptotic expansion of derangement polynomials in terms of Touchard polynomials
Original research paper. Pages 832–842
Mohammad Ghorbani, Mehdi Hassani, Hossein Moshtagh
Full paper (PDF, 241 Kb) | Abstract
In this paper we study the polynomial
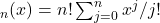
, which is a variant of derangement polynomials. First we obtain an asymptotic expansion for
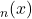
with coefficients in terms of Touchard polynomials. Then, we compute the moments
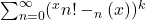
for any integer
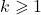
and any real
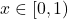
.
Some new results on the largest cycle consisting of quadratic residues
Original research paper. Pages 843–850
Prabin Das and Pinkimani Goswami
Full paper (PDF, 216 Kb) | Abstract
The length of the largest cycle consisting of quadratic residues of a positive integer

is denoted by
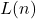
. In this paper, we have obtained a formula for finding
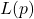
, where

is a prime. Also, we attempt to characterize a prime number

in terms of the largest cycle consisting of quadratic residues of

.
Some new arithmetic functions
Original research paper. Pages 851–856
József Sándor and Krassimir Atanassov
Full paper (PDF, 164 Kb) | Abstract
We introduce and study some new arithmetic functions, connected with the classical functions
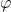
(Euler’s totient),
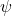
(Dedekind’s function) and
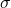
(sum of divisors function).
Factors of alternating convolution of the Gessel numbers
Original research paper. Pages 857–868
Jovan Mikić
Full paper (PDF, 212 Kb) | Abstract
The Gessel number
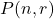
is the number of lattice paths in the plane with
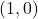
and
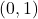
steps from
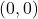
to
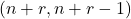
that never touch any of the points from the set
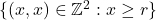
. We show that there is a close relationship between Gessel numbers
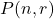
and super Catalan numbers
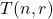
. A new class of binomial sums, so called
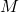
sums, is used. By using one form of the Pfaff–Saalschütz theorem, a new recurrence relation for
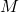
sums is proved. Finally, we prove that an alternating convolution of Gessel numbers
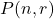
multiplied by a power of a binomial coefficient is always divisible by
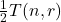
.
Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
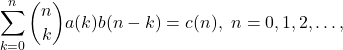
![]() , that is, of the equation
, that is, of the equation ![]() in
in ![]() , where
, where ![]() is the binomial convolution. These expressions are classified as recursive, explicit, determinant, exponential generating function and convolutional expressions. These expressions are compared with those under the usual Cauchy convolution. Several special cases and examples of combinatorial nature are also discussed.
is the binomial convolution. These expressions are classified as recursive, explicit, determinant, exponential generating function and convolutional expressions. These expressions are compared with those under the usual Cauchy convolution. Several special cases and examples of combinatorial nature are also discussed.![]() and their connection with some combinatorial numbers
and their connection with some combinatorial numbers![]()
![]() satisfy certain conditions. This result is a generalization of the work done by Spencer in [11] to count the number of solutions to inequalities of the form
satisfy certain conditions. This result is a generalization of the work done by Spencer in [11] to count the number of solutions to inequalities of the form![]()
![]()


