Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Euler sine product and the continued fraction of π
Original research paper. Pages 463–478
Rahul Verma, V. Puneeth, Joseph Varghese Kureethara and Ashish Sharma
Full paper (PDF, 3702 Kb) | Abstract
The Euler sine product and the continued fraction of
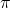
are discussed in this article. Some of the infinite series for cotangent and its derivative are obtained by implementing the concept of Euler sine product and some of the standard series are derived as the immediate consequence of the main results. Furthermore, the continued fraction for odd powers of
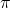
similar to the expression of
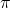
derived by Brouncker is presented in this article. Meanwhile, an expression relating the Basel’s constant and the cotangent function is obtained as follows:
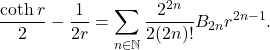
Towards a new generalized Simson’s identity
Original research paper. Pages 479–490
A. G. Shannon, H. M. Srivastava and József Sàndor
Full paper (PDF, 870 Kb) | Abstract
This paper is an attempt to develop an elegant and simple generalization of what is usually called Simson’s Identity, with variations named after Cassini, Catalan and Gelin-Cesàro. It can shed a new light on Simson’s identity, and possibly how to extend it to some reciprocals of these identities and how to generalize it to arbitrary order with some conjectures.
A formal operator involving Fermatian numbers
Original research paper. Pages 491–498
Carlos M. da Fonseca and Anthony G. Shannon
Full paper (PDF, 200 Kb) | Abstract
In this note, old and new properties of Fermatian numbers
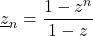
are recalled. A new formal operator is defined and some identities and extensions are discussed.
Evaluation of certain families of log-cosine integrals using hypergeometric function approach and applications
Original research paper. Pages 499–515
Mohammad Idris Qureshi and Shakir Hussain Malik
Full paper (PDF, 288 Kb) | Abstract
In this paper, we provide the analytical solutions of the families of certain definite integrals:
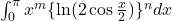
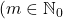
and
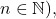
in terms of multiple hypergeometric functions of Kampé de Fériet having the arguments
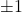
and Riemann zeta functions. As applications, we obtain some mixed summation formulas (19), (35) and (46) involving generalized hypergeometric functions
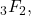
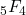
and
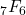
having the arguments
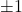
and other (possibly) new summation formulas (38) and (40) for multiple hypergeometric functions of Kampé de Fériet having the arguments
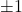
also mixed relations (36) and (47) involving Riemann zeta functions.
The congruence xn ≡ – an (mod m): Solvability and related OEIS sequences
Original research paper. Pages 516–529
Jorma K. Merikoski, Pentti Haukkanen, Timo Tossavainen
Full paper (PDF, 223 Kb) | Abstract
We study the solvability of the congruence
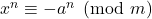
, where
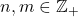
,
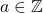
, and
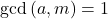
. Our motivation arises from computer experiments concerning a geometric property of the roots of the congruence
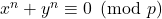
, where
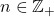
and
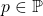
. We encounter several OEIS sequences. We also make new observations on some of them.
A partial recurrence Fibonacci link
Original research paper. Pages 530–537
Anthony G. Shannon, Hakan Akkuş, Yeşim Aküzüm, Ömür Deveci and Engin Özkan
Full paper (PDF, 770 Kb) | Abstract
The purpose of this note is to develop a conjecture for a Fibonacci number generating function in terms of the elements of a second-order two parameter partial recurrence relation which arose in an operations research problem on Poisson distributed lead time in inventory control.
On positive sequences of reals whose block sequence has an asymptotic distribution function
Original research paper. Pages 538–546
József Bukor, Ferdinánd Filip and János T. Tóth
Full paper (PDF, 201 Kb) | Abstract
In this paper we study the properties of the unbounded sequence
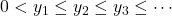
of positive reals having asymptotic distribution function of the form
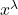
. As a consequence, we immediately get information on the asymptotic behavior of the power means of order
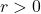
of function values of some arithmetic functions, e.g., the first

prime numbers or the values of the prime counting function.
Lower bounds on expressions dependent on functions φ(n), ψ(n) and σ(n), II
Original research paper. Pages 547–556
Stoyan Dimitrov
Full paper (PDF, 195 Kb) | Abstract
In this paper we establish lower bounds on several expressions dependent on functions
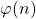
,
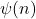
and
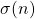
.
Divisibility of the sums of the power of consecutive integers
Original research paper. Pages 557–574
Tian-Xiao He and Peter J.-S. Shiue
Full paper (PDF, 253 Kb) | Abstract
We study the divisibility of the sums of the odd power of consecutive integers,
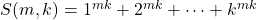
and
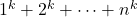
for odd integers
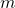
and

, by using the Girard–Waring identity. Faulhaber’s approach for the divisibilities is discussed. Some expressions of power sums in terms of Stirling numbers of the second kind are represented.
On certain inequalities for φ, ψ, σ, and related functions, II
Original research paper. Pages 575–579
József Sàndor
Full paper (PDF, 173 Kb) | Abstract
We offer new proofs and refinements of two inequalities from paper [2]. The unitary functions variants are also considered.
New estimations for numerical analysis approach to twin primes conjecture
Original research paper. Pages 580–586
Gabriele Di Pietro
Full paper (PDF, 195 Kb) | Abstract
This paper provides a better approximation of the functions presented in the article “Numerical Analysis Approach to Twin Primes Conjecture” (see [3]). The new estimates highlight the approximations used in the previous article and the validity of Theorems 1 and 2 through the use of the false hypothesis based on the distribution of primes punctually following the Logarithmic Integral
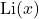
(see [4] and [7], pp. 174–176) will be re-evaluated.
Note on a quadratic inequality
Original research paper. Pages 587–589
Peter Renaud
Full paper (PDF, 144 Kb) | Abstract
In this note we obtain a quadratic inequality based on a result of Atanassov but in a more symmetric form. Somewhat surprisingly, well-known properties of Chebyshev polynomials can be used to give a straightforward proof.
On the set of Set(n)’s
Original research paper. Pages 590–594
Krassimir T. Atanassov
Full paper (PDF, 175 Kb) | Abstract
The set of
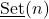
‘s for natural numbers

is constructed. For this set it is proved that it is a commutative semi-group. The conditions for which it is a monoid are given.
A new quadra polynomial sequence
Original research paper. Pages 595–601
Emre Sevgi
Full paper (PDF, 194 Kb) | Abstract
In this paper, we define a new quadra polynomial sequence by using Özkoç numbers as the coefficients. Then, we derive some properties for this polynomial sequence by the help of Fibonacci and Pell polynomials. Additionally, we attempt to define the companion matrix of this polynomial sequence.
Insulated primes
Original research paper. Pages 602–612
Anuraag Saxena and Abhimanyu Kumar
Full paper (PDF, 645 Kb) | Abstract
The degree of insulation of a prime

is defined as the largest interval around

within which no other prime exists. A prime

is classified as insulated if its degree of insulation is greater than that of its neighbouring primes. This leads to the emergence of a new sequence, known as the insulated primes, which starts with 7, 13, 23, 37, 53, 67, 89, 103, 113, 131, 139, 157, 173, 181, 193, 211, 233, 277, 293, and so on. This paper explores several properties and intriguing relationships concerning the degree of insulation, and includes a brief heuristic study of the insulated primes. Finally, the reader is left with a captivating open problem.
Evaluation of the real parts of polylogarithm expressions containing complex arguments via certain logarithmic integrals
Original research paper. Pages 613–633
Narendra Bhandari
Full paper (PDF, 314 Kb) | Abstract
New Fibonacci-type pulsated sequences. Part 2
Original research paper. Pages 634–639
Lilija Atanassova and Velin Andonov
Full paper (PDF, 163 Kb) | Abstract
A new Fibonacci sequence from a pulsated type is introduced. The explicit form of its members is given.
Double domination number of graphs generated from unary products
Original research paper. Pages 640–653
M. Magima and P. Ragukumar
Full paper (PDF, 251 Kb) | Abstract
A subset
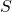
of
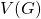
is a double dominating set of a graph

if
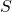
dominates every vertex of

at least twice. The minimum cardinality of a double dominating set denoted by
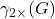
, is the double domination number of

. In this paper, we identified the double domination number of graphs generated by applying various unary operations on standard graph classes.
On the number of partitions of a number into distinct divisors
Original research paper. Pages 654–661
Noah Lebowitz-Lockard and Joseph Vandehey
Full paper (PDF, 204 Kb) | Abstract
Let
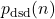
be the number of partitions of

into distinct squarefree divisors of

. In this note, we find a lower bound for
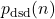
, as well as a sequence of

for which
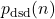
is unusually large.
Book review: “Tertions: Strange Algebraic Objects”
Book review. Pages 662
Anthony G. Shannon
Book review (PDF, 305 Kb)
Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
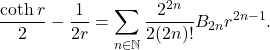
![]()
![]() for first four orders, specifically
for first four orders, specifically ![]() and
and ![]() by constructing certain logarithmic integrals. To extract the real parts, we demonstrate an organized approach, and the proofs solely rely on the calculation of the logarithmic integrals. Additionally, we present a potential closed form of
by constructing certain logarithmic integrals. To extract the real parts, we demonstrate an organized approach, and the proofs solely rely on the calculation of the logarithmic integrals. Additionally, we present a potential closed form of ![]()


