Volume 30, 2024, Number 2

Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 (Online First)

MIN-turns and MAX-turns in k-Dyck paths: A pure generating function approach
Original research paper. Pages 213–222
Helmut Prodinger
Full paper (PDF, 188 Kb) | Abstract

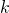
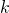
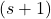
$k$ -Dyck paths differ from ordinary Dyck paths by using an up-step of length $k$ . We analyze at which level the path is after the $s$ -th up-step and before the $(s+1)$ -st up-step. In honour of Rainer Kemp who studied a related concept 40 years ago, the terms max-terms and min-terms are used. Results are obtained by an appropriate use of trivariate generating functions; practically no combinatorial arguments are used.

Some new results on the negative polynomial Pell’s equation
Original research paper. Pages 223–235
K. Anitha, I. Mumtaj Fathima, and A. R. Vijayalakshmi
Full paper (PDF, 259 Kb) | Abstract

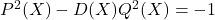
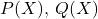
We consider the negative polynomial Pell’s equation $P^2(X)-D(X)Q^2(X)=-1$ , where $D(X)\in \mathbb{Z}[X]$ be some fixed, monic, square-free, even degree polynomials. In this paper, we investigate the existence of polynomial solutions $P(X), \, Q(X)$ with integer coefficients.

Sequences in finite fields yielding divisors of Mersenne, Fermat and Lehmer numbers, II
Original research paper. Pages 236–252
A. M. S. Ramasamy
Full paper (PDF, 284 Kb) | Abstract

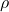
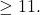
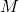
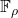
Let $\rho$ be an odd prime $\ge 11.$ In Part I, starting from an $M$ -cycle in a finite field $\mathbb{F}_\rho$ , we have established how the divisors of Mersenne, Fermat and Lehmer numbers arise. The converse question is taken up in this Part with the introduction of an arithmetic function and the notion of a split-associated prime.

On some identities for the DGC Leonardo sequence
Original research paper. Pages 253–270
Çiğdem Zeynep Yılmaz and Gülsüm Yeliz Saçlı
Full paper (PDF, 261 Kb) | Abstract

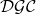
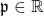
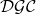
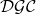
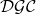
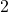
In this study, we examine the Leonardo sequence with dual-generalized complex ( $\mathcal{DGC}$ ) coefficients for $\mathfrak{p} \in \mathbb R$ . Firstly, we express some summation formulas related to the $\mathcal{DGC}$ Fibonacci, $\mathcal{DGC}$ Lucas, and $\mathcal{DGC}$ Leonardo sequences. Secondly, we present some order- $2$ characteristic relations, involving d’Ocagne’s, Catalan’s, Cassini’s, and Tagiuri’s identities. 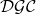The essential point of the paper is that one can reduce the calculations of the $\mathcal{DGC}$ Leonardo sequence by considering $\mathfrak{p}$ . 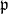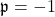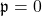This generalization gives the dual-complex Leonardo sequence for $\mathfrak p =-1$ , hyper-dual Leonardo sequence for $\mathfrak p =0$ , and dual-hyperbolic Leonardo sequence for $\mathfrak p =1$ .

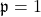
The generalized order (k,t)-Mersenne sequences in groups
Original research paper. Pages 271–282
E. Mehraban, Ö. Deveci, E. Hincal
Full paper (PDF, 302 Kb) | Abstract

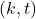
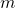
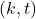
The purpose of this paper is to determine the algebraic properties of finite groups via a Mersenne-like sequence. Firstly, we introduce the generalized order $(k,t)$ -Mersenne number sequences and study the periods of these sequences modulo $m$ . Then, we get some interesting structural results. 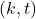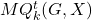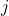Furthermore, we expand the generalized order $(k,t)$ -Mersenne number sequences to groups and we give the definition of the generalized order $(k,t)$ -Mersenne sequences, $MQ_k^t(G,X)$ , in the $j$ -generator groups and also, investigate these sequences in the non-Abelian finite groups in detail. 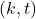At last, we obtain the periods of the generalized order $(k,t)$ -Mersenne sequences in some special groups as applications of the results produced.

Some infinite series summations involving linear recurrence relations of order 2 and 3
Original research paper. Pages 283–310
Anthony G. Shannon, Peter J.-S. Shiue, Shen C. Huang, Ali Balooch, Yu-Chung Liu
Full paper (PDF, 319 Kb) | Abstract

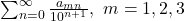
This paper extends known results of second and third order recursive sequences through extensive formulations of properties of the roots of their characteristic equations, some are old but most are new. They are applied to novel studies of $\sum_{n=0}^{\infty}{\frac{a_{mn}}{10^{n+1}}, \ m=1,2,3}$ , including their convergence criteria, and applied to many standard sequences, as particular cases of a generic $\left\{a_n\right\}$ . 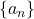The detailed development of the algebra of the pertinent theorems, and their associated lemmas and corollaries, should open up new vistas for interested number theorists with the concluding results on series values.

The error term of the sum of digital sum functions in arbitrary bases
Original research paper. Pages 311–318
Erdenebileg Erdenebat and Ka Lun Wong
Full paper (PDF, 219 Kb) | Abstract

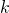
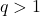
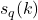
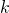
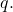
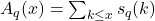
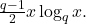
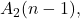
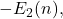
Let $k$ be a non-negative integer and $q > 1$ be a positive integer. Let $s_q(k)$ be the sum of digits of $k$ written in base $q.$ In 1940, Bush proved that $A_q(x)=\sum_{k \leq x} s_q (k)$ is asymptotic to $\frac{q-1}{2}x \log_q x.$ In 1968, Trollope proved an explicit formula for the error term of $A_2(n-1),$ labeled by $-E_2(n),$ where $n$ is a positive integer. 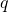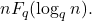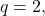In 1975, Delange extended Trollope’s result to an arbitrary base $q$ by another method and labeled the error term $nF_q(\log_q n).$ When $q=2,$ the two formulas of the error term are supposed to be equal, but they look quite different. We proved directly that those two formulas are equal. 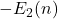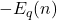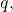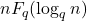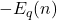More interestingly, Cooper and Kennedy in 1999 applied Trollope’s method to extend $-E_2(n)$ to $-E_q(n)$ with a general base $q,$ and we also proved directly that $nF_q(\log_q n)$ and $-E_q(n)$ are equal for any $q.$

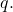
On some series involving the binomial coefficients 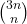$\binom{3n}{n}$
Original research paper. Pages 319–334
Kunle Adegoke, Robert Frontczak and Taras Goy
Full paper (PDF, 280 Kb) | Abstract

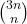
Using a simple transformation, we obtain much simpler forms for some series involving binomial coefficients $\binom{3n}n$ derived by Necdet Batır. New evaluations are given and connections with Fibonacci numbers and the golden ratio are established. Finally we derive some Fibonacci and Lucas series involving the reciprocals of $\binom{3n}n$ .

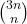
Infinite multisets: Basic properties and cardinality
Original research paper. Pages 335–356
Milen V. Velev
Full paper (PDF, 1.8 Mb) | Abstract

This research work presents the topic of infinite multisets, their basic properties and cardinality from a somewhat different perspective. In this work, a new property of multisets, ‘m-cardinality’, is defined using multiset functions. M-cardinality unifies and generalizes the definitions of cardinality, injection, bijection, and surjection to apply to multisets. M-cardinality takes into account both the number of distinct elements in a multiset and the number of copies of each element (i.e., the multiplicity of the elements). Based on m-cardinality, ‘m-cardinal numbers’ are defined as a generalization of cardinal numbers in the context of multisets. Some properties of m-cardinal numbers associated with finite and infinite msets have been researched. Concrete examples of transfinite m-cardinal numbers are given, corresponding to infinite msets which are less than ℵ₀ (the cardinality of the countably infinite set). It has been established that between finite numbers and ℵ₀ there exist hierarchies of transfinite m-cardinals, corresponding to infinite msets. Furthermore, there are examples of infinite msets with negative multiplicity that have a cardinality less than zero. We prove that there is a decreasing sequence of transfinite m-cardinal numbers, corresponding to infinite msets with negative multiplicity, and in this sequence, there is not a smallest transfinite m-cardinal number.

A generalization of arithmetic derivative to p-adic fields and number fields
Original research paper. Pages 357–382
Brad Emmons and Xiao Xiao
Full paper (PDF, 315 Kb) | Abstract

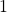
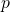
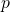
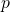
The arithmetic derivative is a function from the natural numbers to itself that sends all prime numbers to $1$ and satisfies the Leibniz rule. The arithmetic partial derivative with respect to a prime $p$ is the $p$ -th component of the arithmetic derivative. In this paper, we generalize the arithmetic partial derivative to $p$ -adic fields (the local case) and the arithmetic derivative to number fields (the global case). 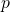We study the dynamical system of the $p$ -adic valuation of the iterations of the arithmetic partial derivatives. 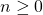We also prove that for every integer $n\geq 0$ , there are infinitely many elements with exactly $n$ anti-partial derivatives. 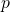In the end, we study the $p$ -adic continuity of arithmetic derivatives.

Melham’s sums for some Lucas polynomial sequences
Original research paper. Pages 383–409
Chan-Liang Chung and Chunmei Zhong
Full paper (PDF, 295 Kb) | Abstract

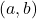
A Lucas polynomial sequence is a pair of generalized polynomial sequences that satisfy the Lucas recurrence relation. Special cases include Fibonacci polynomials, Lucas polynomials, and Balancing polynomials. We define the $(a,b)$ -type Lucas polynomial sequences and prove that their Melham’s sums have some interesting divisibility properties. Results in this paper generalize the original Melham’s conjectures.

On certain bounds for the divisor function
Original research paper. Pages 410–417
József Sándor
Full paper (PDF, 222 Kb) | Abstract

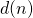
We offer various bounds for the divisor function $d(n)$ , in terms of $n$ , or other arithmetical functions.

On certain relations among the generating functions for certain quadratic forms
Original research paper. Pages 418–426
K. R. Vasuki and P. Nagendra
Full paper (PDF, 213 Kb) | Abstract

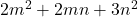
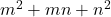
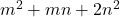
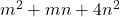
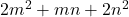
The object of this article is to establish the relation between the generating function of the quadratic form $2m^2+2mn+3n^2$ {and} the generating function{s} for the quadratic forms $m^2+mn+n^2$ , $m^2+mn+2n^2$ , $m^2+mn+4n^2$ and $2m^2+mn+2n^2$ . In the process, we deduce certain interesting theta function identities.

On the distribution of powerful and $r$ -free lattice points
Original research paper. Pages 427–435
Sunanta Srisopha and Teerapat Srichan
Full paper (PDF, 246 Kb) | Abstract

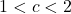
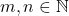
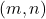
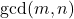
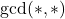
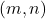
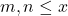
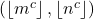
Let $1<c<2$ . For $m, n \in \mathbb{N}$ , a lattice point $(m, n)$ is powerful if and only if $\gcd(m, n)$ is a powerful number, where $\gcd(*, *)$ is the greatest common divisor function. In this paper, we count the number of the ordered pairs $(m,n)$ , $m, n \leq x$ such that the lattice point $(\left\lfloor m^c \right\rfloor, \left\lfloor n^c \right\rfloor)$ is powerful. Moreover, we study $r$ -free lattice points analogues of powerful lattice points.

On unitary Zumkeller numbers
Original research paper. Pages 436–442
Bhabesh Das
Full paper (PDF, 428 Kb) | Abstract

It is well known that if n is a Zumkeller number, then the positive divisors of n can be partitioned into two disjoint subsets of equal sum. Similarly for unitary Zumkeller number n, the unitary divisors of n can be partitioned into two disjoint subsets of equal sum. In this article, we have derived some results related to unitary Zumkeller number, unitary half-Zumkeller number and also presented some numerical examples.

On tertions and dual numbers
Original research paper. Pages 443–452
Krassimir T. Atanassov
Full paper (PDF, 211 Kb) | Abstract

In a previous author’s paper [1], the mathematical object called “tertion” was discussed. Some operations over tertions were introduced and their properties were studied. There, it was showed that the complex numbers and quaternions can be represented by tertions. Here, we show that the dual numbers also are representable by tertions. The concept of a “0-quaternion” is introduced and its representation by tertions is given. Ideas for future research are described.

Multiplicative Sombor index of trees
Original research paper. Pages 453–460
Nasrin Dehgardi, Zhibin Du and Yilun Shang
Full paper (PDF, 196 Kb) | Abstract

For a graph $\Omega$ , the multiplicative Sombor index is defined as

$\prod_{SO}(\Omega)=\prod_{ab\in \mathcal{E}(\Omega)}\sqrt{d^2_\Omega(a)+d^2_\Omega(b)},$

where $d_\Omega(a)$ is the degree of vertex $a$ . Liu [Liu, H. (2022). Discrete Mathematics Letters, 9, 80–85] showed that, when $\mathcal{T}$ is a tree of order $n$ , $\prod_{SO}(\mathcal{T})\geqslant \prod_{SO}(P_n)=5(\sqrt{8})^{n-3}$ . We improved this result and show that, if $\mathcal{T}$ is a tree of order $n$ with maximum degree $\cal{D}$ , then

$\prod_{SO}(\mathcal{T})\geqslant \left\{\begin{array}{ll} (5({\cal{D}}^2+4))^{\frac{\cal{D}}{2}}8^{\frac{n-2{\cal{D}}-1}{2}} & {\rm if}\;{\cal{D}}\leqslant\frac{n-1}{2},\\[2mm] ({\cal{D}}^2+1)^{\frac{2{\cal{D}}+1-n}{2}}(5({\cal{D}}^2+4))^{\frac{n-{\cal{D}}-1}{2}} & {\rm if}\;{\cal{D}}>\frac{n-1}{2}. \end{array}\right.$

Also, we show that equality holds if and only if $\mathcal{T}$ is a spider whose all legs have length less than three or all legs have length more than one.

Corrigendum to “Two arithmetic functions related to Euler’s and Dedekind’s functions”. [Notes on Number Theory and Discrete Mathematics, 30(1), 179–183]
Corrigendum. Pages 461–462
Krassimir Atanassov
Corrigendum (PDF, 139 Kb)

Volume 30 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 (Online First)

Latest Issue

Journal Contents