Sunanta Srisopha and Teerapat Srichan
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 30, 2024, Number 2, Pages 427–435
DOI: 10.7546/nntdm.2024.30.2.427-435
Full paper (PDF, 246 Kb)
Details
Authors and affiliations
Sunanta Srisopha ![]()
![]()
Department of Mathematics, Faculty of Science,
Valaya Alongkorn Rajabhat University under the Royal Patronage Pathum Thani Province,
Pathumthani 13180, Thailand
Teerapat Srichan ![]()
![]()
Department of Mathematics, Faculty of Science,
Kasetsart University
Bangkok 10900, Thailand
Abstract
Let ![]() . For
. For ![]() , a lattice point
, a lattice point ![]() is powerful if and only if
is powerful if and only if ![]() is a powerful number, where
is a powerful number, where ![]() is the greatest common divisor function. In this paper, we count the number of the ordered pairs
is the greatest common divisor function. In this paper, we count the number of the ordered pairs ![]() ,
, ![]() such that the lattice point
such that the lattice point ![]() is powerful. Moreover, we study
is powerful. Moreover, we study ![]() -free lattice points analogues of powerful lattice points.
-free lattice points analogues of powerful lattice points.
Keywords
- Greatest common divisor
- Piatetski-Shapiro sequence
 -free lattice points
-free lattice points
2020 Mathematics Subject Classification
- 11N37
- 11N45
References
- Akbal, Y. (2017). Friable values of Piatetski-Shapiro sequences. Proceedings of the American Mathematical Society, 145(10), 4255–4268.
- Baker, R., Banks, W., Brudern, J., Shparlinski, I., & Weingartner, A. (2013). Piatetski-Shapiro sequences. Acta Arithmetica, 1(157), 37–68.
- Cao, X., & Zhai, W. (1998). The distribution of square-free numbers of the form
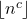 . Journal de théorie des nombres de Bordeaux, 10(2), 287–299.
. Journal de théorie des nombres de Bordeaux, 10(2), 287–299. - Deshouillers, J. M. (2019). A remark on cube-free numbers in Segal–Piatestki-Shapiro sequences. Hardy–Ramanujan Journal, 41, 127–132.
- Dimitrov, S. I. (2022). Exponential sums over Piatetski-Shapiro primes in arithmetic progressions. Preprint. arXiv:2211.10928.
- Dimitrov, S. I. (2022). Primes of the form
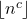 with square-free
with square-free 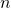 . Preprint. arXiv:2207.09808.
. Preprint. arXiv:2207.09808. - Dimitrov, S. I. (2022). A Bombieri–Vinogradov type result for exponential sums over Piatetski-Shapiro primes. Lithuanian Mathematical Journal, 62(4), 435–446.
- Guo, V. Z., Li, J., & Zhang, M. (2023). Piatetski-Shapiro primes in arithmetic progressions. The Ramanujan Journal, 60(3), 677–692.
- Guo, V. Z., & Qi, J. (2022). A Generalization of Piatetski-Shapiro Sequences. Taiwanese Journal of Mathematics, 26(1), 33–47.
- Ivić. A, (1985). The Theory of the Riemann Zeta Function. Wiley, New York.
- Li, J., Zhang, M., & Xue, F. (2022). An additive problem over Piatetski-Shapiro primes and almost-primes. The Ramanujan Journal, 57(4), 1307–1333.
- Liu, K., Shparlinski, I. E., & Zhang, T. (2017). Squares in Piatetski-Shapiro sequences. Acta Arithmetica, 181, 239–252.
- Ma, S. (2022). On the distribution of k-full lattice points in
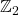 . AIMS Mathematics, 7(6), 10596–10608.
. AIMS Mathematics, 7(6), 10596–10608. - Pyatetskii-Shapiro, I. I. (1953). On the distribution of prime numbers in sequences of the form ⌊f(n)⌋. Matematicheskii Sbornik, 75(3), 559–566.
- Rieger, G. (1978). Remark on a paper of Stux concerning squarefree numbers in non-linear sequences. Pacific Journal of Mathematics, 78(1), 241–242.
- Srichan, T. (2021). On the distribution of (k, r)-integers in Piatetski-Shapiro sequences. Czechoslovak Mathematical Journal, 71(4), 1063–1070.
- Srichan, T., & Tangsupphathawat, P. (2020). Square-full numbers in Piatetski-Shapiro sequences. Annales mathématiques du Québec, 44, 385–391.
- Stux, I. (1975). Distribution of squarefree integers in non-linear sequences. Pacific Journal of Mathematics, 59(2), 577–584.
- Wang, H., & Zhang, Y. (2023). On the divisor function over Piatetski-Shapiro sequences. Czechoslovak Mathematical Journal, 73(2), 613–620.
- Zhang, M., & Li, J. (2017). Distribution of cube-free numbers with form
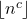 . Frontiers of Mathematics in China, 12(6), 1515–1525.
. Frontiers of Mathematics in China, 12(6), 1515–1525.
Manuscript history
- Received: 11 April 2023
- Revised: 6 June 2024
- Accepted: 14 June 2024
- Online First: 20 June 2024
Copyright information
![]() Ⓒ 2024 by the Authors.
Ⓒ 2024 by the Authors.
This is an Open Access paper distributed under the terms and conditions of the Creative Commons Attribution 4.0 International License (CC BY 4.0).
Related papers
Cite this paper
Srisopha, S., & Srichan, T. (2024). On the distribution of powerful and r-free lattice points. Notes on Number Theory and Discrete Mathematics, 30(2), 427-435, DOI: 10.7546/nntdm.2024.30.2.427-435.


