Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Bounds on some energy-like invariants of corona and edge corona of graphs
Original research paper. Pages 383–398
Chinglensana Phanjoubam and Sainkupar Mn Mawiong
Full paper (PDF, 199 Kb) | Abstract
The Laplacian-energy-like invariant of a finite simple graph is the sum of square roots of all its Laplacian eigenvalues and the incidence energy is the sum of square roots of all its signless Laplacian eigenvalues. In this paper, we give the bounds on the Laplacian-energy-like invariant and incidence energy of the corona and edge corona of two graphs. We also observe that the bounds on the Laplacian-energy-like invariant and incidence energy of the corona and edge corona are sharp when the graph is the corona or edge corona of two complete graphs.
On linear algebra of one type of symmetric matrices with harmonic Fibonacci entries
Original research paper. Pages 399–410
Mücahit Akbıyık, Seda Yamaç Akbıyık and Fatih Yılmaz
Full paper (PDF, 209 Kb) | Abstract
This paper focuses on a specially constructed matrix whose entries are harmonic Fibonacci numbers and considers its Hadamard exponential matrix. A lot of admiring algebraic properties are presented for both of them. Some of them are determinant, inverse in usual and in the Hadamard sense, permanents, some norms, etc. Additionally, a MATLAB-R2016a code is given to facilitate the calculations and to further enrich the content.
Bi-unitary multiperfect numbers, IV(c)
Original research paper. Pages 411–434
Pentti Haukkanen
Full paper (PDF, 287 Kb) | Abstract
A divisor
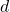
of a positive integer

is called a unitary divisor if
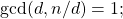
and
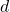
is called a bi-unitary divisor of

if the greatest common unitary divisor of
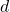
and
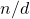
is unity. The concept of a bi-unitary divisor is due to D. Surynarayana (1972). Let
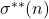
denote the sum of the bi-unitary divisors of

. A positive integer

is called a bi-unitary multiperfect number if
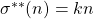
for some
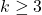
. For
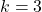
we obtain the bi-unitary triperfect numbers.
Peter Hagis (1987) proved that there are no odd bi-unitary multiperfect numbers. The present paper is part IV(c) in a series of papers on even bi-unitary multiperfect numbers. In parts I, II and III we determined all bi-unitary triperfect numbers of the form 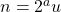 , where
, where 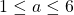 and
and 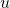 is odd. In part V we fixed the case
is odd. In part V we fixed the case 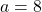 . The case
. The case 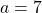 is more difficult. In Parts IV(a-b) we solved partly this case, and in the present paper (Part IV(c)) we continue the study of the same case (
is more difficult. In Parts IV(a-b) we solved partly this case, and in the present paper (Part IV(c)) we continue the study of the same case (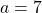 ).
).
Note on the natural density of r-free numbers
Original research paper. Pages 435–440
Sunanta Srisopha, Teerapat Srichan and Sukrawan Mavecha
Full paper (PDF, 230 Kb) | Abstract
Let P be a finite set of prime numbers. By using an elementary method, the proportion of all r-free numbers which are divisible by at least one element in P is studied.
Number of stable digits of any integer tetration
Original research paper. Pages 441–457
Marco Ripà and Luca Onnis
Full paper (PDF, 1147 Kb) | Abstract
In the present paper we provide a formula that allows to compute the number of stable digits of any integer tetration base
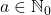
. The number of stable digits, at the given height of the power tower, indicates how many of the last digits of the (generic) tetration are frozen. Our formula is exact for every tetration base which is not coprime to
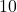
, although a maximum gap equal to
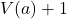
digits (where
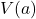
denotes the constant congruence speed of

) can occur, in the worst-case scenario, between the upper and lower bound. In addition, for every
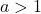
which is not a multiple of
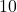
, we show that
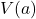
corresponds to the
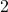
-adic or
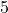
-adic valuation of
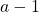
or
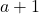
, or even to the
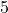
-adic order of
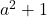
, depending on the congruence class of

modulo
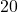
.
On complex Leonardo numbers
Original research paper. Pages 458–465
Adnan Karataş
Full paper (PDF, 149 Kb) | Abstract
In this study, we introduce the complex Leonardo numbers and give some of their properties including Binet formula, generating function, Cassini and d’Ocagne’s identities. Also, we calculate summation formulas for complex Leonardo numbers involving complex Fibonacci and Lucas numbers.
Binomial sums with k-Jacobsthal and k-Jacobsthal–Lucas numbers
Original research paper. Pages 466–476
A. D. Godase
Full paper (PDF, 213 Kb) | Abstract
In this paper, we derive some important identities involving k-Jacobsthal and k-Jacobsthal–Lucas numbers. Moreover, we use multinomial theorem to obtain distinct binomial sums of k-Jacobsthal and k-Jacobsthal–Lucas numbers.
Generalized Pisano numbers
Original research paper. Pages 477–490
Yüksel Soykan, İnci Okumuş and Erkan Taşdemir
Full paper (PDF, 196 Kb) | Abstract
In this paper, we define and investigate the generalized Pisano sequences and we deal with, in detail, two special cases, namely, Pisano and Pisano–Lucas sequences. We present Binet’s formulas, generating functions and Simson’s formulas for these sequences. Moreover, we give some identities and matrices associated with these sequences. Furthermore, we show that there are close relations between Pisano and Pisano–Lucas numbers and modified Oresme, Oresme–Lucas and Oresme numbers.
On the derivatives of B-Tribonacci polynomials
Original research paper. Pages 491–499
Suchita Arolkar
Full paper (PDF, 167 Kb) | Abstract
In this paper, B-Tribonacci polynomials which are extensions of Fibonacci polynomials are defined. Some identities relating B-Tribonacci polynomials and their derivatives are established.
Average value of some certain types of arithmetic functions with Piatetski-Shapiro sequences
Original research paper. Pages 500–506
Suphawan Janphaisaeng, Teerapat Srichan and Pinthira Tangsupphathawat
Full paper (PDF, 170 Kb) | Abstract
In this paper, we study asymptotic behaviour of the sum
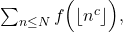
where
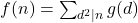
under three different types of assumptions on
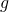
and
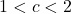
.
Some aspects of interchanging difference equation orders
Original research paper. Pages 507–516
Anthony G. Shannon and Engin Özkan
Full paper (PDF, 592 Kb) | Abstract
This paper builds on Roettger and Williams’ extensions of the primordial Lucas sequence to consider some relations among difference equations of different orders. This paper utilises some of their second and third order recurrence relations to provide an excursion through basic second order sequences and related third order recurrence relations with a variety of numerical illustrations which demonstrate that mathematical notation is a tool of thought.
On edge irregularity strength of line graph and line cut-vertex graph of comb graph
Original research paper. Pages 517–524
H. M. Nagesh and V. R. Girish
Full paper (PDF, 172 Kb) | Abstract
For a simple graph

, a vertex labeling
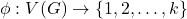
is called

-labeling. The weight of an edge
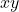
in

, written
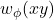
, is the sum of the labels of end vertices
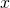
and
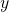
, i.e.,
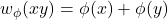
. A vertex

-labeling is defined to be an edge irregular

-labeling of the graph

if for every two different edges

and
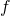
,
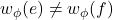
. The minimum

for which the graph

has an edge irregular

-labeling is called the edge irregularity strength of

, written
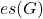
. In this paper, we find the exact value of edge irregularity strength of line graph of comb graph

for
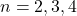
; and determine the bounds for
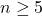
. Also, the edge irregularity strength of line cut-vertex graph of

for
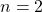
; and determine the bounds for
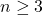
.
On certain rational perfect numbers, II
Original research paper. Pages 525–532
József Sándor
Full paper (PDF, 171 Kb) | Abstract
We continue the study from [1], by studying equations of type
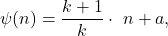
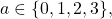
and
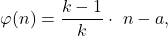
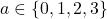
for
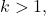
where
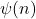
and
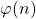
denote the Dedekind, respectively Euler’s, arithmetical functions.
Some congruences on the hyper-sums of powers of integers involving Fermat quotient and Bernoulli numbers
Original research paper. Pages 533–541
Fouad Bounebirat and Mourad Rahmani
Full paper (PDF, 174 Kb) | Abstract
For a given prime p ≥ 5, let ℤp denote the set of rational p-integers (those rational numbers whose denominator is not divisible by p). In this paper, we establish some congruences modulo a prime power p5 on the hyper-sums of powers of integers in terms of Fermat quotient, Wolstenholme quotient, Bernoulli and Euler numbers.
An introduction to harmonic complex numbers and harmonic hybrid Fibonacci numbers: A unified approach
Original research paper. Pages 542–557
Emel Karaca and Fatih Yılmaz
Full paper (PDF, 230 Kb) | Abstract
The purpose of this paper is to define and construct new number systems, called the harmonic complex Fibonacci sequences (HCF) and the harmonic hybrid Fibonacci (HHF) sequences. These sequences are defined by inspiring the well-known harmonic and hybrid numbers in literature. We give some fundamental definitions and theorems about these sequences in detail. Moreover, we examine some algebraic properties such as Binet-like-formula, partial sums related to these sequences. Finally, we provide a Maple 13 source code to verify the sequences easily.
Objects generated by an arbitrary natural number. Part 2: Modal aspect
Original research paper. Pages 558–563
Krassimir T. Atanassov
Full paper (PDF, 158 Kb) | Abstract
The set Set(n), generated by an arbitrary natural number n, was defined in [2] and some arithmetic functions, defined over its elements are introduced in an algebraic aspect. Here, over the elements of Set(n), two arithmetic functions similar to the modal type of operators are defined and some of their basic properties are studied.
Identities involving some special numbers and polynomials on p-adic integral
Original research paper. Pages 564–574
Neşe Ömür, Sibel Koparal, Ömer Duran and Kübra Nur Südemen
Full paper (PDF, 192 Kb) | Abstract
In this paper, we get new identities involving Bernoulli, Daehee and Stirling numbers, and their representations by using p-adic integrals and combinatorial techniques.
On a new additive arithmetic function related to a fixed integer
Original research paper. Pages 575–580
Mihoub Bouderbala and Meselem Karras
Full paper (PDF, 160 Kb) | Abstract
The main purpose of this paper is to define a new additive arithmetic function related to a fixed integer
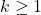
and to study some of its properties. This function is given by
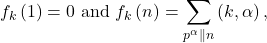
such that 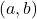 denotes the greatest common divisor of the integers
denotes the greatest common divisor of the integers  and
and 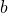 .
.
Eisenstein series of level 6 and level 10 with their applications to theta function identities of Ramanujan
Original research paper. Pages 581–588
A. I. Vijaya Shankar
Full paper (PDF, 174 Kb) | Abstract
S. Ramanujan recorded theta function identities of different levels in the unorganized pages of his second notebook and the lost notebook. In this paper, we prove level 6 and level 10 theta function identities by using Eisenstein series identities.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP3/43/2021.
Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
![]() , where
, where ![]() and
and ![]() is odd. In part V we fixed the case
is odd. In part V we fixed the case ![]() . The case
. The case ![]() is more difficult. In Parts IV(a-b) we solved partly this case, and in the present paper (Part IV(c)) we continue the study of the same case (
is more difficult. In Parts IV(a-b) we solved partly this case, and in the present paper (Part IV(c)) we continue the study of the same case (![]() ).
).![]()
![]() denotes the greatest common divisor of the integers
denotes the greatest common divisor of the integers ![]() and
and ![]() .
.

