Average value of some certain types of arithmetic functions with Piatetski-Shapiro sequences

Suphawan Janphaisaeng, Teerapat Srichan and Pinthira Tangsupphathawat
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 3, Pages 500–506
DOI: 10.7546/nntdm.2022.28.3.500-506
Full paper (PDF, 170 Kb)

Details

Authors and affiliations

Suphawan Janphaisaeng
Department of Mathematics, Faculty of Science, Naresuan University
Phitsanulok 65000, Thailand

Teerapat Srichan
Department of Mathematics, Faculty of Science, Kasetsart University
Bangkok 10900, Thailand

Pinthira Tangsupphathawat
Department of Mathematics, Faculty of Science and Technology, Phranakorn Rajabhat University
Bangkok 10220, Thailand

Abstract

In this paper, we study asymptotic behaviour of the sum \sum_{n\leq N}{f}\Big(\lfloor n^c \rfloor\Big), where f(n)=\sum_{d^2\mid n}g(d) under three different types of assumptions on g and 1<c<2.

Keywords

  • Arithmetic function
  • Piatetski-Shapiro sequences

2020 Mathematics Subject Classification

  • 11N37
  • 11N69

References

  1. Akbal, Y. (2017). Friable values of Piatetski-Shapiro sequences. Proceedings of the American Mathematical Society, 145, 4255–4268.
  2. Baker, R. C., & Banks, W. D. (2015). Character sums with Piatetski-Shapiro sequences. The Quarterly Journal of Mathematics, 66, 393–416.
  3. Baker, R. C., Banks, W. D., Brüdern, J., Shparlinski, I. E., & Weingartner, A. (2013). Piatetski-Shapiro sequences. Acta Arithmetica, 157, 37–68.
  4. Banks, W. D., Guo, V. Z., & Shparlinski, I. E. (2016). Almost primes of the form 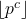\lfloor p^c \rfloor. Indagationes Mathematicae, 27, 423–436.
  5. Bordellés, O., Dai, L., Heyman, R., Pan, H., & Shparlinski, I. E. (2019). On a sum involving the Euler function. Journal of Number Theory, 202, 278–297.
  6. Cao, X., & Zhai, W. (1998). The distribution of square-free numbers of the form [n^ c]. Journal de Theorie des Nombres de Bordeaux, 10(2), 287–299.
  7. Deshouillers, J. M. (2019). A remark on cube-free numbers in Segal–Piatestki-Shapiro sequences. Hardy–Ramanujan Journal, 41, 127–132.
  8. Ivić, A. (1985) The Riemann Zeta-function: The Theory of the Riemann Zeta-function with Applications. John Wiley & Sons, Inc., New York.
  9. Liu, K., Shparlinski, I. E., & Zhang, T. (2017). Squares in Piatetski-Shapiro sequences. Acta Arithmetica, 181, 239–252.
  10. Ma, J., Wu, J., & Zhao, F. (2021). On a generalisation of Bordellés–Dai–Heyman–Pan–Shparlinski’s conjecture. Journal of Number Theory, 236, 334–348.
  11. Piatetski-Shapiro, I. I. (1953). On the distribution of prime numbers in sequences of the form 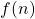f(n). Math. Sbornik, 33, 559–566.
  12. Rieger, G. (1978). Remark on a paper of Stux concerning squarefree numbers in non-linear sequences. Pacific Journal of Mathematics, 78(1), 241–242.
  13. Srichan, T. (2021). On the Distribution of (k, r)-Integers in Piatetski-Shapiro Sequences. Czechoslovak Mathematical Journal, 71(4), 1063–1070.
  14. Srichan, T. Multiplicative functions of special type on Piatetski-Shapiro sequences. Mathematica Slovaca (to appear).
  15. Srichan, T., & Tangsupphathawat, P. (2020). Square-full numbers in Piatetski-Shapiro sequences. Annales mathématiques du Québec, 44(2), 385–391.
  16. Stux, I. (1975). Distribution of squarefree integers in non-linear sequences. Pacific Journal of Mathematics, 59(2), 577–584.
  17. Wu, J. (2020). Note on a paper by Bordellés, Dai, Heyman, Pan and Shparlinski. Periodica Mathematica Hungarica, 80, 95–102.
  18. Zhai, W. (2020). On a sum involving the Euler function. Journal of Number Theory, 211, 199–219.
  19. Zhang, M., & Jinjiang, L. (2017). Distribution of cube-free numbers with form [n^c]. Frontiers of Mathematics in China, 12(6), 1515–1525.
  20. Zhao, F., & Wu, J. (2022). Note on a paper by Bordellés, Dai, Heyman, Pan and Shparlinski, II. Acta Arithmetica, 202, 185–194.

Manuscript history

  • Received: 2 March 2022
  • Revised: 25 July 2022
  • Accepted: 2 August 2022
  • Online First: 4 August 2022

Related papers

Cite this paper

Janphaisaeng, S., Srichan, T., & Tangsupphathawat, P. (2022). Average value of some certain types of arithmetic functions with Piatetski-Shapiro sequences. Notes on Number Theory and Discrete Mathematics, 28(3), 500-506, DOI: 10.7546/nntdm.2022.28.3.500-506.

Comments are closed.