Volume 31 ▶ Number 1 ▷ Number 2 (Online First)
A quantum calculus framework for Gaussian Fibonacci and Gaussian Lucas quaternion numbers
Original research paper. Pages 1–14
Bahar Kuloğlu
Full paper (PDF, 1037 Kb) | Abstract
In order to investigate the relationship between Gaussian Fibonacci numbers and quantum numbers and to develop both a deeper theoretical understanding in this study, q-Gaussian Fibonacci, q-Gaussian Lucas quaternions and polynomials are taken with quantum integers by bringing a different perspective. Based on these definitions, the Binet formula of these number sequences is found, and some algebraic properties, important theorems, propositions and identities related to the formula are given. Thus, new perspectives are obtained in the analysis and applications of complex systems.
A note on Chebyshev’s theorem
Original research paper. Pages 15–26
A. Bërdëllima
Full paper (PDF, 262 Kb) | Abstract
We revisit a classical theorem of Chebyshev about distribution of primes on intervals
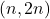
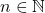
, and prove a generalization of it. Extending Erdős’ arithmetical-combinatorial argument, we show that for all
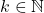
, there is
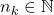
such that the intervals
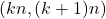
contain a prime for all

. A quantitative lower bound is derived for the number of primes on such intervals. We also give numerical upper bounds for
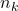
for
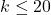
, and we draw comparisons with existing results in the literature.
Some fundamental Fibonacci number congruences
Original research paper. Pages 27–40
Anthony G. Shannon, Tian-Xiao He, Peter J.-S. Shiue, and Shen C. Huang
Full paper (PDF, 963 Kb) | Abstract
This paper investigates a number of congruence properties related to the coefficients of a generalized Fibonacci polynomial. This polynomial was defined to produce properties comparable with those of the standard polynomials of some special functions. Some of these properties are compared with known identities, while others are seemingly characteristic of arbitrary order recurrences. These include generalizations of, and analogies for, results of Appell, Bernoulli, Euler, Hilton, Horadam and Williams. In turn, the theorems lead to conjectures for further development.
On tridimensional Lucas-balancing numbers and some properties
Original research paper. Pages 41–53
J. Chimpanzo, P. Catarino and M. V. Otero-Espinar
Full paper (PDF, 212 Kb) | Abstract
In this article, we introduce the tridimensional version of the Lucas-balancing numbers based on the unidimensional version, and we also study some of their properties and sum identities.
Euclidean tours in fairy chess
Original research paper. Pages 54–68
Gabriele Di Pietro and Marco Ripà
Full paper (PDF, 254 Kb) | Abstract
The present paper aims to generalize the Knight’s tour problem for
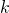
-dimensional grids of the form
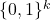
by considering other fairy chess leapers. Accordingly, we constructively show the existence of closed tours in
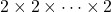
(
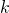
times) chessboards concerning the Wazir, the Threeleaper, and the Zebra, for all

. This extends the recent discovery of Euclidean Knight’s tours on these grids to the above-mentioned leapers, opening a new research direction on fairy chess leapers performing fixed-length jumps on regular grids.
A note on the approximation of divisor functions
Original research paper. Pages 69–72
József Sándor
Full paper (PDF, 198 Kb) | Abstract
We offer an arithmetic proof of a result from the recent paper [1]. A more general result is provided, too.
A note on a bivariate Leonardo sequence
Original research paper. Pages 73–78
Carlos M. da Fonseca and Anthony G. Shannon
Full paper (PDF, 160 Kb) | Abstract
Recently, quite a few generalizations of Leonardo numbers have emerged in the literature. In this short note, we propose a new bivariate extension and provide its generating function. We correct the generating function of another recently proposed bivariate generalization.
Correction notice to “Leonardo’s bivariate and complex polynomials” [Notes on Number Theory and Discrete Mathematics, 2022, Volume 28, Number 1, Pages 115–123]
Original research paper. Pages 79–81
Efruz Özlem Mersin
Correction notice (PDF, 139 Kb)
Series associated with harmonic numbers, Fibonacci numbers and central binomial coefficients 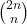
Original research paper. Pages 82–90
Segun Olofin Akerele and Olamide Esther Salami
Full paper (PDF, 265 Kb) | Abstract
We find various series that involve the central binomial coefficients
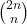
, harmonic numbers and Fibonacci numbers. Contrary to the traditional hypergeometric function
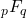
approach, our method utilizes a straightforward transformation to obtain new evaluations linked to Fibonacci numbers and the golden ratio. We also gave a new series representation for
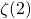
.
New properties of arithmetic functions related to gcd and lcm
Original research paper. Pages 91–97
Brahim Mittou
Full paper (PDF, 219 Kb) | Abstract
This paper explores additional properties of the arithmetic functions
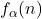
and
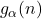
, defined respectively by
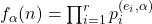
and
![Rendered by QuickLaTeX.com g_\alpha(n) = \prod_{i=1}^r p_i^{[e_i, \alpha]}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-2a54c8d1e86ce9ee40a58e4559eb2e89_l3.png)
, where
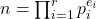
is the prime factorization of a positive integer
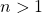
,
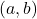
and
![Rendered by QuickLaTeX.com [a, b]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-b28ebca9266518f1a778b4a4b102a2e1_l3.png)
denote, respectively the greatest common divisor and the least common multiple of any two integers

and
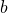
. These functions and some of their properties have been introduced and investigated in previous works. In this paper, we establish several new theorems that reveal deeper insights into the relationships between these functions.
Josephus Nim
Original research paper. Pages 98–112
Shoei Takahashi, Hikaru Manabe and Ryohei Miyadera
Full paper (PDF, 223 Kb) | Abstract
In this study, we propose a variant of Nim that uses two piles. In the first pile, we have stones with a weight of

, and in the second pile, we have stones with a weight of
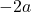
, where

is a natural number. Two players take turns to remove stones from one of the piles. The total weight of the stones to be removed should be equal to or less than half of the total weight of the stones in the pile. Therefore, if there are
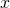
stones with weight

and
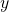
stones with weight
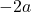
, then the total weight of the stones to be removed is less than or equal to
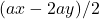
. The player who removes the last stone is the winner of the game. The authors proved that when
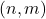
is the winning position of the previous player,
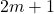
is the last remaining number in the Josephus problem, where there are
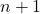
numbers, and every second number is to be removed. For any natural number

, there are similar relationships between the position at which the Grundy number is

and the
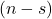
-th removed number in the Josephus problem with
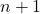
numbers.
Almost neo cobalancing numbers
Original research paper. Pages 113–126
Ahmet Tekcan and Ecem Akgüç
Full paper (PDF, 232 Kb) | Abstract
In this work, we determined the general terms of almost neo cobalancing numbers, almost Lucas-neo cobalancing numbers and almost neo cobalancers in terms of cobalancing and Lucas-cobalancing numbers. We also deduced some results on relationship with Pell, Pell–Lucas, triangular and square triangular numbers. Further we formulate the sum of first

terms of these numbers.
On the extensions of two arithmetical functions and some of their properties
Original research paper. Pages 127–132
Mladen Vassilev-Missana and Peter Mladenov Vassilev
Full paper (PDF, 246 Kb) | Abstract
In the paper, an extension of the well-known Jordan’s totient function and generalized Dedekind psi-function are proposed and some properties of theirs are studied.
Power Fibonacci sequences in quadratic integer modulo m
Original research paper. Pages 133–145
Ryan A. Longhas, Cyryn Jade L. Prendol, Jenelyn F. Bantilan, and Larra L. De Leon
Full paper (PDF, 246 Kb) | Abstract
The power Fibonacci sequence in
![Rendered by QuickLaTeX.com \mathbb{Z}_m[\sqrt{\delta}]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-77a6b286cb411e550a084dae87d04f5c_l3.png)
is defined as a Fibonacci sequence \linebreak
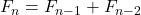
where
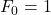
and
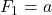
, such that
![Rendered by QuickLaTeX.com a\in \mathbb{Z}_m[\sqrt{\delta}]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-6e1ab517ec448d5d8cd8098014604243_l3.png)
and
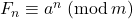
, for all
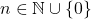
. In this paper, we investigated the existence of power Fibonacci sequences in
![Rendered by QuickLaTeX.com \mathbb{Z}_m[\sqrt{\delta}]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-77a6b286cb411e550a084dae87d04f5c_l3.png)
, and the number of power Fibonacci sequences in
![Rendered by QuickLaTeX.com \mathbb{Z}_m[\sqrt{\delta}]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-77a6b286cb411e550a084dae87d04f5c_l3.png)
for a given
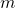
, where
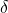
is a square-free integer. Furthermore, we determined explicitly all power Fibonacci sequences in
![Rendered by QuickLaTeX.com \mathbb{Z}_{p^k}[\sqrt{\delta}]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-5ad48ea6e2ffcdcb7647ff7046e0fc19_l3.png)
, where
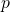
is a prime number.
On the set of Set(n)’s. Part 2
Original research paper. Pages 146–156
Krassimir T. Atanassov
Full paper (PDF, 243 Kb) | Abstract
In the previous author’s research, the set of
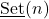
‘s for natural numbers

was constructed. For this set it was proved that it is a commutative semi-group. The condition for which it is a monoid was given. The present leg of research continues by demonstrating that for any
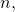
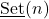
is a lattice, and by the introduction of four new operations over the elements of
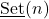
.
On Entry 8 of Chapter 19 of Ramanujan’s Second Notebook
Original research paper. Pages 157–165
K. R. Vasuki and A. Darshan
Full paper (PDF, 194 Kb) | Abstract
The aim of this paper is to give an alternative proof of Entry 8 of Chapter 19 of Ramanujan’s Second Notebook. Further, we deduce certain modular equations of degree 5 as a consequence of Entry 8 of Chapter 19.
Some formulas related to Euler’s product expansion for cosine function
Original research paper. Pages 166–180
Taekyun Kim and Dae San Kim
Full paper (PDF, 263 Kb) | Abstract
In this paper, we derive by using elementary methods some continued fractions, certain identities involving derivatives of
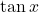
, several expressions for
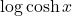
and an identity for
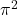
, from a series expansion of
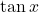
, which gives the product expansion of the cosine function.
Diophantine equations with Lucas and Fibonacci number coefficients
Original research paper. Pages 181–190
Cemil Karaçam, Alper Vural, Bilal Aytepe, and Ferhat Yıldız
Full paper (PDF, 239 Kb) | Abstract
Fibonacci and Lucas numbers are special number sequences that have been the subject of many studies throughout history due to the relations they provide. The studies are continuing today, and findings about these number sequences are constantly increasing. The relations between the Fibonacci and Lucas numbers, which were found during the proof of the prime between two consecutive numbers belonging to the Fibonacci or Lucas number sequence with the Euclidean algorithm, started our project. In the project, Diophantine equations whose coefficients are Lucas or Fibonacci numbers have been studied, various relations have been found, and their proofs have been made.
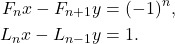
As in the above example, the equivalents of 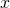 and
and 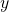 values were found in the Diophantine equations with Fibonacci and Lucas number coefficients; and based on this example, different variations of the Diophantine equations whose coefficients were selected from the Fibonacci and Lucas number sequences were created, and their proofs were made.
values were found in the Diophantine equations with Fibonacci and Lucas number coefficients; and based on this example, different variations of the Diophantine equations whose coefficients were selected from the Fibonacci and Lucas number sequences were created, and their proofs were made.
Secondly, the geometric shapes consisting of vertices determined by pair of numbers selected from the Fibonacci or Lucas number sequence were considered, and their properties were examined. Various relations were found between them, and generalizations were made.
Padovan and Perrin numbers of the form 
Original research paper. Pages 191–200
Djamel Bellaouar, Özen Özer and Noureddine Azzouza
Full paper (PDF, 290 Kb) | Abstract
Consider the Padovan sequence
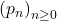
given by
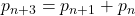
with
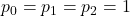
. Its companion sequence, the Perrin sequence
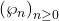
, follows the same recursive formula as the Padovan numbers, but with different initial values:
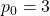
,
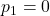
and
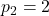
. In this paper, we leverage Baker’s theory concerning nonzero linear forms in logarithms of algebraic numbers along with a reduction procedure that employs the theory of continued fractions. This enables us to explicitly identify all Padovan and Perrin numbers that conform to the representation

, where
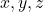
and
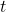
are positive integers with
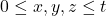
.
This volume of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP6/12/02.12.2024.
Volume 31 ▶ Number 1 ▷ Number 2 (Online First)
![]()
![]()
![]() and
and ![]() values were found in the Diophantine equations with Fibonacci and Lucas number coefficients; and based on this example, different variations of the Diophantine equations whose coefficients were selected from the Fibonacci and Lucas number sequences were created, and their proofs were made.
values were found in the Diophantine equations with Fibonacci and Lucas number coefficients; and based on this example, different variations of the Diophantine equations whose coefficients were selected from the Fibonacci and Lucas number sequences were created, and their proofs were made.![]()


