Volume 28, 2022, Number 2

Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

On wide-output sieves
Original research paper. Pages 147–158
Alessandro Cotronei
Full paper (PDF, 282 Kb) | Abstract

We describe and compare several novel sieve-like methods. They assign values of several functions (i.e., the prime omega functions ω and Ω and the divisor function d) to each natural number in the considered range of integer numbers. We prove that in some cases the algorithms presented have a relatively small computational complexity. A more detailed output is indeed obtained with respect to the original Sieve of Eratosthenes.

Remark on the transcendence of real numbers generated by Thue–Morse along squares
Original research paper. Pages 159–166
Eiji Miyanohara
Full paper (PDF, 205 Kb) | Abstract

In 1929, Mahler proved that the real number generated by Thue–Morse sequence is transcendental. Later, Adamczewski and Bugeaud gave a different proof of the transcendence of this number using a combinatorial transcendence criterion. Moreover, Kumar and Meher gave the generalization of the combinatorial transcendence criterion under the subspace Lang conjecture. In this paper, we prove under the subspace Lang conjecture that the real number generated by Thue–Morse along squares is transcendental by using the combinatorial transcendence criterion of Kumar and Meher.

A generalization of multiple zeta values. Part 1: Recurrent sums
Original research paper. Pages 167–199
Roudy El Haddad
Full paper (PDF, 340Kb) | Abstract

Multiple zeta star values have become a central concept in number theory with a wide variety of applications. In this article, we propose a generalization, which we will refer to as recurrent sums, where the reciprocals are replaced by arbitrary sequences. We introduce a toolbox of formulas for the manipulation of such sums. We begin by developing variation formulas that allow the variation of a recurrent sum of order m to be expressed in terms of lower order recurrent sums. We then proceed to derive theorems (which we will call inversion formulas) which show how to interchange the order of summation in a multitude of ways. Later, we introduce a set of new partition identities in order to then prove a reduction theorem which permits the expression of a recurrent sum in terms of a combination of non-recurrent sums. Finally, we use these theorems to derive new results for multiple zeta star values and recurrent sums of powers.

A generalization of multiple zeta values. Part 2: Multiple sums
Original research paper. Pages 200–233
Roudy El Haddad
Full paper (PDF, 348 Kb) | Abstract

Multiple zeta values have become of great interest due to their numerous applications in mathematics and physics. In this article, we present a generalization, which we will refer to as multiple sums, where the reciprocals are replaced with arbitrary sequences. We develop formulae to help with manipulating such sums. We develop variation formulae that express the variation of multiple sums in terms of lower order multiple sums. Additionally, we derive a set of partition identities that we use to prove a reduction theorem that expresses multiple sums as a combination of simple sums. 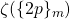We present a variety of applications including applications concerning polynomials and MZVs such as generating functions and expressions for $\zeta(\{2p\}_m)$ and $\zeta^\star(\{2p\}_m)$ . 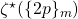Finally, we establish the connection between multiple sums and a type of sums called recurrent sums. By exploiting this connection, we provide additional partition identities for odd and even partitions.

Note on some sequences having periods that divide (p^p − 1) / (p − 1)
Original research paper. Pages 234–239
Abdelkader Benyattou and Miloud Mihoubi
Full paper (PDF, 185 Kb) | Abstract

In this paper, we use the properties of the classical umbral calculus to determine sequences related to the Bell numbers and having periods divide $\left(p^{ \, p}-1\right) / \left(p-1\right)$ .

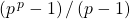
On the equation f(n² − Dnm + m²) = f²(n) − Df(n)f(m) + f²(m)
Original research paper. Pages 240–251
B. M. Phong and R. B. Szeidl
Full paper (PDF, 192 Kb) | Abstract

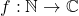
We give all solutions $f:\Bbb N \to \Bbb C$ of the functional equation

$f(n^2-Dnm+m^2)=f^2(n)-Df(n)f(m)+f^2(m),$

where $D\in\{1,2\}$ .

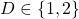Some equalities and binomial sums about the generalized Fibonacci number u_n
Original research paper. Pages 252–260
Yücel Türker Ulutaş and Derya Toy
Full paper (PDF, 146 Kb) | Abstract

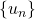
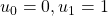
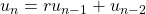
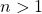
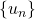
In this study, we take the generalized Fibonacci sequence $\{u_{n}\}$ as $u_{0}=0,u_{1}=1$ and $\ u_{n}=ru_{n-1}+u_{n-2}$ for $n>1$ , where $r$ is a non-zero integer. Based on Halton’s paper in [4], we derive three interrelated functions involving the terms of generalized Fibonacci sequence $\{u_{n}\}$ . Using these three functions we introduce a simple approach to obtain a lot of identities, binomial sums and alternate binomial sums involving the terms of generalized Fibonacci sequence $\{u_{n}\}$ .

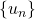
q-Fibonacci bicomplex and q-Lucas bicomplex numbers
Original research paper. Pages 261–275
Fügen Torunbalcı Aydın
Full paper (PDF, 252 Kb) | Abstract

In the paper, we define the q-Fibonacci bicomplex numbers and the q-Lucas bicomplex numbers, respectively. Then, we give some algebraic properties of the q-Fibonacci bicomplex numbers and the q-Lucas bicomplex numbers.

A note on the Aiello–Subbarao conjecture on addition chains
Original research paper. Pages 276–280
Hatem M. Bahig
Full paper (PDF, 231 Kb) | Abstract

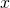
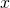
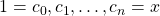
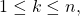
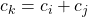
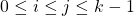
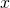
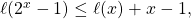
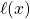
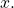
Given a positive integer $x$ , an addition chain for $x$ is an increasing sequence of positive integers $1=c_0,c_1, \ldots , c_n=x$ such that for each $1\leq k\leq n,$ $c_k=c_i+c_j$ for some $0\leq i\leq j\leq k-1$ . In 1937, Scholz conjectured that for each positive integer $x$ , $\ell(2^x-1) \leq \ell(x)+ x-1,$ where $\ell(x)$ denotes the minimal length of an addition chain for $x.$ In 1993, Aiello and Subbarao stated the apparently stronger conjecture that there is an addition chain for 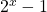$2^x-1$ with length equals to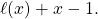 $\ell(x)+x-1.$ We note that the Aiello–Subbarao conjecture is not stronger than the Scholz (also called the Scholz–Brauer) conjecture.

On certain rational perfect numbers
Original research paper. Pages 281–285
József Sándor
Full paper (PDF, 146 Kb) | Abstract

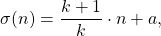
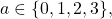
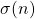
We study equations of type $\sigma(n) = \dfrac{k+1}{k} \cdot n+a,$ where $a\in \{0, 1, 2, 3\},$ where $k$ and $n$ are positive integers, while $\sigma(n)$ denotes the sum of divisors of $n.$

Perfect squares in the sum and difference of balancing-like numbers
Original research paper. Pages 286–301
M. K. Sahukar, Zafer Şiar, Refik Keskin and G. K. Panda
Full paper (PDF, 231 Kb) | Abstract

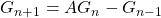
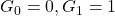
In this study, we deal with the existence of perfect powers which are sum and difference of two balancing numbers. Moreover, as a generalization we explore the perfect squares which are sum and difference of two balancing-like numbers, where balancing-like sequence is defined recursively as $G_{n+1}=AG_n-G_{n-1}$ with initial terms $G_0=0,G_1=1$ for $A \geq 3$ .

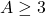
About the theorem that partially solves the Navarrete–Orellana Conjecture
Original research paper. Pages 302–317
Jorge Andrés Julca Avila and Gabriel Silva de Andrade
Full paper (PDF, 344 Kb) | Abstract

The Navarrete–Orellana Conjecture states that “given a large prime number a sequence is generated, in such a way that all odd prime numbers, except the given prime, are fixed points of that sequence”. In this work, we formulated a theorem that partially confirms the veracity of this conjecture, more specifically, all prime numbers of a given line segment are fixed points of this sequence.

On hyperbolic k-Jacobsthal and k-Jacobsthal–Lucas octonions
Original research paper. Pages 319–330
Engin Özkan and Mine Uysal
Full paper (PDF, 344 Kb) | Abstract

In this work, we investigate the hyperbolic k-Jacobsthal and k-Jacobsthal–Lucas octonions. We give Binet’s Formula, Cassini’s identity, Catalan’s identity, d’Ocagne identity, generating functions of the hyperbolic k-Jacobsthal and k-Jacobsthal–Lucas octonions. Also, we present many properties of these octonions.

Two 2-Fibonacci sequences generated by a mixed scheme. Part 1
Original research paper. Pages 331–338
Krassimir T. Atanassov
Full paper (PDF, 227 Kb) | Abstract

A new scheme of 2-Fibonacci sequences is introduced and the explicit formulas for its n-th members are given. For difference of all previous sequences from Fibonacci type, the present 2-Fibonacci sequences are obtained by a new way. It is proved that the new sequences have bases with 48 elements about function 𝜑 and modulo 9.

The Hadamard-type k-step Pell sequences
Original research paper. Pages 339–349
Ömür Deveci, ‪Yeşim Aküzüm and Muhammad Eshaq Rashedi
Full paper (PDF, 239 Kb) | Abstract

In this paper, we define the Hadamard-type k-step Pell sequence by using the Hadamard-type product of characteristic polynomials of the Pell sequence and the k-step Pell sequence. Also, we derive the generating matrices for these sequences, and then we obtain relationships between the Hadamard-type k-step Pell sequences and these generating matrices. Furthermore, we produce the Binet formula for the Hadamard-type k-step Pell numbers for the case that k is odd integers and k ≥ 3. Finally, we derive some properties of the Hadamard-type k-step Pell sequences such as the combinatorial representation, the generating function, and the exponential representation by using its generating matrix.

Notes on efficient computation of Ramanujan cubic equations
Original research paper. Pages 350–375
Peter J.-S. Shiue, Anthony G. Shannon, Shen C. Huang, Jorge E. Reyes
Full paper (PDF, 335 Kb) | Abstract

This paper considers properties of a theorem of Ramanujan to develop properties and algorithms related to cubic equations. The Ramanujan cubics are related to the Cardano cubics and Padovan recurrence relations. These generate cubic identities related to heptagonal triangles and third order recurrence relations, as well as an algorithm for finding the real root of the relevant Ramanujan cubic equation. The algorithm is applied to, and analyzed for, some of the earlier examples in the paper.

On certain equations and inequalities involving the arithmetical functions φ(n) and d(n)
Original research paper. Pages 376–379
József Sándor and Saunak Bhattacharjee
Full paper (PDF, 152 Kb) | Abstract

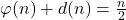
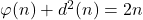
By using the results and methods of \cite {3}, we will study the equation $\varphi(n) + d(n) = \frac{n}{2}$ and the related inequalities. The equation $\varphi(n) + d^2(n)=2n$ will be solved, too.

Corrigendum to “On upper Hermite–Hadamard inequalities for geometric-convex and log-convex functions” [Notes on Number Theory and Discrete Mathematics, 2014, Vol. 20, No. 5, 25–30]
Corrigendum. Pages 380–381
József Sándor
Full paper (PDF, 101 Kb)

This volume of the International Journal “Notes on Number Theory and Discrete Mathematics”
is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No.
KP-06-NP3/43/2021.

Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Latest Issue

Journal Contents