József Sándor and Saunak Bhattacharjee
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 2, Pages 376–379
DOI: 10.7546/nntdm.2022.28.2.376-379
Full paper (PDF, 152 Kb)
Details
Authors and affiliations
József Sándor 
Babeș-Bolyai University, Department of Mathematics
Cluj-Napoca, Romania
Saunak Bhattacharjee
Indian Institute of Science Education and Research
Tirupati, India
Abstract
By using the results and methods of [1], we will study the equation 
and the related inequalities. The equation 
will be solved, too.
Keywords
- Arithmetic functions
- Inequalities
2020 Mathematics Subject Classification
- 11A25
References
- Sándor, J. (2020). On the equation
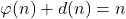and related inequalities. Notes on Number Theory and Discrete Mathematics, 26(3), 1–4. - Sándor, J., & Atanassov, K. T. (2021). Arithmetic Functions. Nova Science Publishers, New York.
- Sándor, J., & Kovács, L. (2009). An inequality for the number of divisors. Octogon Mathematical Magazine, 17(2), 746–749.
- Sándor, J., Mitrinović, D. S., & Crstici, B. (2005). Handbook of Number Theory I. Springer.
Manuscript history
- Received: 10 January 2022
- Revised: 27 May 2022
- Accepted: 9 June 2022
- Online First: 14 June 2022
Related papers
- Sándor, J. (2014). On certain inequalities for σ, φ, ψ and related functions. Notes on Number Theory and Discrete Mathematics, 20 (2), 52–60.
- Sándor, J. (2020). On the equation φ(n) + d(n) = n and related inequalities. Notes on Number Theory and Discrete Mathematics, 26 (3), 1-4.
- Sándor, J. (2023). On certain equations and inequalities involving the arithmetical functions φ(n) and d(n) – II. Notes on Number Theory and Discrete Mathematics, 29(1), 130-136.
Cite this paper
Sándor, J. & Bhattacharjee, S. (2022). On certain equations and inequalities involving the arithmetical functions φ(n) and d(n). Notes on Number Theory and Discrete Mathematics, 28(2), 376-379, DOI: 10.7546/nntdm.2022.28.2.376-379.
