Roudy El Haddad
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 2, Pages 200–233
DOI: 10.7546/nntdm.2022.28.2.200-233
Full paper (PDF, 348 Kb)
Details
Authors and affiliations
Roudy El Haddad ![]()
![]()
Engineering Department, La Sagesse University
Beirut, Lebanon
Abstract
Multiple zeta values have become of great interest due to their numerous applications in mathematics and physics. In this article, we present a generalization, which we will refer to as multiple sums, where the reciprocals are replaced with arbitrary sequences. We develop formulae to help with manipulating such sums. We develop variation formulae that express the variation of multiple sums in terms of lower order multiple sums. Additionally, we derive a set of partition identities that we use to prove a reduction theorem that expresses multiple sums as a combination of simple sums. We present a variety of applications including applications concerning polynomials and MZVs such as generating functions and expressions for ![]() and
and ![]() . Finally, we establish the connection between multiple sums and a type of sums called recurrent sums. By exploiting this connection, we provide additional partition identities for odd and even partitions.
. Finally, we establish the connection between multiple sums and a type of sums called recurrent sums. By exploiting this connection, we provide additional partition identities for odd and even partitions.
Keywords
- Multiple sums
- Viète’s formula
- Polynomials
- Generating function
- Multiple zeta values
- Riemann zeta function
- Partitions
- Stirling numbers
- Bernoulli numbers
- Faulhaber formula
2020 Mathematics Subject Classification
- 11P84
- 11B73
- 11M32
- 11C08
References
- Andrews, G. E. (1998). The Theory of Partitions, Vol. 2. Cambridge University Press.
- Aoki, T., Ohno, Y., & Wakabayashi, N. (2011). On generating functions of multiple zeta values and generalized hypergeometric functions. Manuscripta Mathematica, 134(1), 139–155.
- Arfken, G. B., & Weber, H. J. (2000). Mathematical Methods for Physicists, 5th Edition. Academic Press.
- Bernoulli, J. (1689). Propositiones arithmeticae de seriebus infinitis earumque summa finita [Arithmetical propositions about infinite series and their finite sums]. Basel, J. Conrad.
- Bernoulli, J. (1713). Ars Conjectandi, Opus Posthumum; Accedit Tractatus De Seriebus Infinitis, Et Epistola Gallice scripta De Ludo Pilae Reticularis [Theory of inference, posthumous work. With the Treatise on infinite series… ]. Thurnisii.
- Bernoulli, J. (1742). Corollary III of de Seriebus Varia. Opera Omnia. Lausanne & Basel: Marc-Michel Bousquet & co. 4:8.
- Blümlein, J., Broadhurst, D., & Vermaseren, J. A. (2010). The multiple zeta value data mine. Computer Physics Communications, 181(3), 582–625.
- Blümlein, J., & Kurth, S. (1999). Harmonic sums and Mellin transforms up to two-loop order. Physical Review D, 60(1), 014018.
- Broadhurst, D. (1986). Exploiting the 1, 440-fold symmetry of the master two-loop diagram. Zeitschrift für Physik C Particles and Fields, 32(2), 249–253.
- Broadhurst, D. (2013). Multiple zeta values and modular forms in quantum field theory. In Computer Algebra in Quantum Field Theory, Springer, 33–73.
- Bruinier, J. H., & Ono, K. (2013). Algebraic formulas for the coefficients of half-integral weight harmonic weak Maass forms. Advances in Mathematics, 246, 198–219.
- Chapman, R. (1999). Evaluating ζ(2). Preprint. Available online at: https://empslocal.ex.ac.uk/people/staff/rjchapma/etc/zeta2.pdf.
- Euler, L. (1740). De summis serierum reciprocarum [On the sums of series of reciprocals]. Commentarii academiae scientiarum Petropolitanae, 7, 123–134. Opera Omnia, Series, 1, 73–86. Available online at: https://scholarlycommons.pacific.edu/euler-works/41 .
- Euler, L. (1743). Demonstration de la somme de cette suite
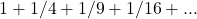 [Demonstration of the sum of the series
[Demonstration of the sum of the series 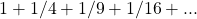 ]. Journal litteraire d’Allemagne, de Suisse et du Nord, 2, 115–127. Available online at: https://scholarlycommons.pacific.edu/euler-works/63/.
]. Journal litteraire d’Allemagne, de Suisse et du Nord, 2, 115–127. Available online at: https://scholarlycommons.pacific.edu/euler-works/63/. - Euler, L. (1748). Introductio in Analysin Infinitorum, Volume 1 [Introduction to the Analysis of the Infinite, Volume 1]. Lausanne: Marcum-Michaelem Bousquet, Volume 1, pp. 1–320. Available online at: https://scholarlycommons.pacific.edu/euler-works/101/.
- Euler, L. (1776). Meditationes circa singulare serierum genus [Meditations about
a singular type of series]. Novi Commentarii academiae scientiarum Petropolitanae, 20, 140–186. Available online at: https://scholarlycommons.pacific.edu/euler-works/477/. - Euler, L. (1811). De summatione serierum in hac forma contentarum
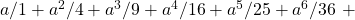 etc. [On the summation of series contained in the form
etc. [On the summation of series contained in the form 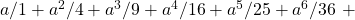 etc.] Memoires de l’académie des sciences de St.-Petersbourg, 3, 26–42. Available online at: https://scholarlycommons.pacific.edu/euler-works/736/.
etc.] Memoires de l’académie des sciences de St.-Petersbourg, 3, 26–42. Available online at: https://scholarlycommons.pacific.edu/euler-works/736/. - Faulhaber, J. (1631). Academia Algebrae, darinnen die miraculosische Inventiones, zu den höchsten Cossen weiters continuirt und profitiert werden, Ulm, Available online at: https://digital.slub-dresden.de/werkansicht/dlf/254/1.
- Granville, A. (1997). A decomposition of Riemann’s zeta-function. London Mathematical Society Lecture Note Series, Cambridge University Press, 95–102.
- El Haddad, R. (2021). Repeated sums and binomial coefficients. Open Journal of Discrete Applied Mathematics, 4(2), 30–47.
- El Haddad, R. (2022). A generalization of multiple zeta values. Part 1: Recurrent sums. Notes on Number Theory and Discrete Mathematics, 28(2), 167–199.
- Hardy, G. H., & Ramanujan, S. (1918). Asymptotic formulae in combinatory analysis. Proceedings of the London Mathematical Society, s2-17(1), 75–115.
- Hoffman, M. E. (1992). Multiple harmonic series. Pacific Journal of Mathematics, 152(2), 275–290.
- Hoffman, M. E. (1997). The algebra of multiple harmonic series. Journal of Algebra, 194(2), 477–495.
- Kassel, C. (2012). Quantum Groups, Vol. 155. Springer Science & Business Media.
- Loeb, D. E. (1992). A generalization of the Stirling numbers. Discrete Mathematics, 103(3), 259–269.
- Mengoli, P. (1650). Praefatio [Preface]. Novae quadraturae arithmeticae, seu de additione fractionum [New arithmetic quadrature (i.e., integration), or on the addition of fractions]. Bologna: Giacomo Monti.
- Nielsen, N. (1923). Traité élémentaire des nombres de Bernoulli. Paris, Gauthier-Villars.
- Ohno, Y., Zagier, D. (2001). Multiple zeta values of fixed weight, depth, and height. Indagationes Mathematicae, 12(4), 483–487.
- Oresme, N. (1961). Quaestiones super geometriam Euclidis, Vol. 3. Brill Archive.
- Propp, J. (1989). Some variants of Ferrers diagrams. Journal of Combinatorial Theory, Series A, 52(1), 98–128.
- Rademacher, H. (1938). On the partition function p(n). Proceedings of the London Mathematical Society, s2-43(1), 241–254.
- Rademacher, H. (1943). On the expansion of the partition function in a series. Annals of Mathematics, 44(3), 416–422.
- Riemann, B. (1974). Appendix on the number of primes less than a given magnitude. Pure and Applied Mathematics, 58, 299–305.
- Schneider, R. (2016). Partition zeta functions. Research in Number Theory, 2(1), 9.
- Viète, F. (1970). Opera Mathematica. Hildesheim-New-York: Georg Olms Verlag (Original work published 1579. Reprinted Leiden, Netherlands, 1646).
- Zagier, D. (1994). Values of zeta functions and their applications. Proceedings of the First European Congress of Mathematics, Paris, July 6–10, 1992, Springer, 497–512.
- Zagier, D. (1995). Multiple zeta values. Unpublished manuscript. Retrieved from: http://people.mpim-bonn.mpg.de/zagier/files/tex/EssenImprovedZetaValues/fulltext.pdf.
- Zlobin, S. A. (2005). Generating functions for the values of a multiple zeta function. Vestnik Moskovskogo Universiteta. Seriya 1. Matematika, Mekhanika, 2, 55–59.
Manuscript history
- Received: 4 February 2021
- Revised: 22 February 2022
- Accepted: 12 April 2022
- Online First: 18 April 2022
Related papers
Cite this paper
El Haddad, R. (2022). A generalization of multiple zeta values. Part 2: Multiple sums. Notes on Number Theory and Discrete Mathematics, 28(2), 200-233, DOI: 10.7546/nntdm.2022.28.2.200-233.


