Roudy El Haddad
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 2, Pages 167–199
DOI: 10.7546/nntdm.2022.28.2.167-199
Full paper (PDF, 340 Kb)
Details
Authors and affiliations
Roudy El Haddad ![]()
![]()
Engineering Department, La Sagesse University
Beirut, Lebanon
Abstract
Multiple zeta star values have become a central concept in number theory with a wide variety of applications. In this article, we propose a generalization, which we will refer to as recurrent sums, where the reciprocals are replaced by arbitrary sequences. We introduce a toolbox of formulas for the manipulation of such sums. We begin by developing variation formulas that allow the variation of a recurrent sum of order m to be expressed in terms of lower order recurrent sums. We then proceed to derive theorems (which we will call inversion formulas) which show how to interchange the order of summation in a multitude of ways. Later, we introduce a set of new partition identities in order to then prove a reduction theorem which permits the expression of a recurrent sum in terms of a combination of non-recurrent sums. Finally, we use these theorems to derive new results for multiple zeta star values and recurrent sums of powers.
Keywords
- Recurrent sums
- Partitions
- Multiple zeta star values
- Riemann zeta function
- Bell polynomials
- Stirling numbers
- Bernoulli numbers
- Faulhaber formula
2020 Mathematics Subject Classification
- 11P84
- 11B73
- 11M32
- 05A18
References
- Andrews, G. E. (1998). The Theory of Partitions, Vol. 2. Cambridge University Press.
- Arfken, G. B., & Weber, H. J. (2000). Mathematical Methods for Physicists, 5th Edition. Academic Press.
- Bernoulli, J. (1689). Propositiones arithmeticae de seriebus infinitis earumque summa finita [Arithmetical propositions about infinite series and their finite sums]. Basel, J. Conrad.
- Bernoulli, J. (1713). Ars Conjectandi, Opus Posthumum; Accedit Tractatus De Seriebus Infinitis, Et Epistola Gallice scripta De Ludo Pilae Reticularis [Theory of inference, posthumous work. With the Treatise on infinite series… ]. Thurnisii.
- Bernoulli, J. (1742). Corollary III of de Seriebus Varia. Opera Omnia. Lausanne & Basel: Marc-Michel Bousquet & co. 4:8.
- Blümlein, J., Broadhurst, D., & Vermaseren, J. A. (2010). The multiple zeta value data mine. Computer Physics Communications, 181(3), 582–625.
- Blümlein, J., & Kurth, S. (1999). Harmonic sums and Mellin transforms up to two-loop order. Physical Review D, 60(1), 014018.
- Broadhurst, D. (1986). Exploiting the 1, 440-fold symmetry of the master two-loop diagram. Zeitschrift für Physik C Particles and Fields, 32(2), 249–253.
- Broadhurst, D. (2013). Multiple zeta values and modular forms in quantum field theory. In Computer Algebra in Quantum Field Theory, Springer, 33–73.
- Bruinier, J. H., & Ono, K. (2013). Algebraic formulas for the coefficients of half-integral weight harmonic weak Maass forms. Advances in Mathematics, 246, 198–219.
- Chapman, R. (1999). Evaluating ζ(2). Preprint. Available online at: https://empslocal.ex.ac.uk/people/staff/rjchapma/etc/zeta2.pdf.
- Euler, L. (1740). De summis serierum reciprocarum [On the sums of series of reciprocals]. Commentarii academiae scientiarum Petropolitanae, 7, 123–134. Opera Omnia, Series, 1, 73–86. Available online at: https://scholarlycommons.pacific.edu/euler-works/41 .
- Euler, L. (1743). Demonstration de la somme de cette suite
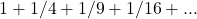 [Demonstration of the sum of the series
[Demonstration of the sum of the series 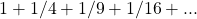 ]. Journal litteraire d’Allemagne, de Suisse et du Nord, 2, 115–127. Available online at: https://scholarlycommons.pacific.edu/euler-works/63/.
]. Journal litteraire d’Allemagne, de Suisse et du Nord, 2, 115–127. Available online at: https://scholarlycommons.pacific.edu/euler-works/63/. - Euler, L. (1748). Introductio in Analysin Infinitorum, Volume 1 [Introduction to the Analysis of the Infinite, Volume 1]. Lausanne: Marcum-Michaelem Bousquet, Volume 1, pp. 1–320. Available online at: https://scholarlycommons.pacific.edu/euler-works/101/.
- Euler, L. (1776). Meditationes circa singulare serierum genus [Meditations about
a singular type of series]. Novi Commentarii academiae scientiarum Petropolitanae, 20, 140–186. Available online at: https://scholarlycommons.pacific.edu/euler-works/477/. - Euler, L. (1811). De summatione serierum in hac forma contentarum
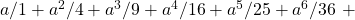 etc. [On the summation of series contained in the form
etc. [On the summation of series contained in the form 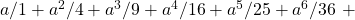 etc.]. Memoires de l’académie des sciences de St.-Petersbourg, 3, 26–42. Available online at: https://scholarlycommons.pacific.edu/euler-works/736/.
etc.]. Memoires de l’académie des sciences de St.-Petersbourg, 3, 26–42. Available online at: https://scholarlycommons.pacific.edu/euler-works/736/. - Faulhaber, J. (1631). Academia Algebrae, darinnen die miraculosische Inventiones, zu den höchsten Cossen weiters continuirt und profitiert werden, Ulm, Available online at: https://digital.slub-dresden.de/werkansicht/dlf/254/1.
- Granville, A. (1997). A decomposition of Riemann’s zeta-function. London Mathematical Society Lecture Note Series, Cambridge University Press, 95–102.
- El Haddad, R. (2021). Repeated sums and binomial coefficients. Open Journal of Discrete Applied Mathematics, 4(2), 30–47.
- El Haddad, R. (2022). Repeated integration and explicit formula for the
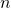 -th integral of
-th integral of 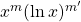 . Open Journal of Mathematical Science (in press).
. Open Journal of Mathematical Science (in press). - El Haddad, R. (2022). A generalization of multiple zeta values. Part 2: Multiple sums. Notes on Number Theory and Discrete Mathematics, 28(2), 200–233.
- Hardy, G. H., & Ramanujan, S. (1918). Asymptotic formulae in combinatory analysis. Proceedings of the London Mathematical Society, s2-17(1), 75–115.
- Hoffman, M. E. (1992). Multiple harmonic series. Pacific Journal of Mathematics, 152(2), 275–290.
- Hoffman, M. E. (1997). The algebra of multiple harmonic series. Journal of Algebra, 194(2), 477–495.
- Hoffman, M. E., & Moen, C. (1996). Sums of triple harmonic series. Journal of Number Theory, 60(2), 329–331.
- Kassel, C. (2012). Quantum Groups, Vol. 155. Springer Science & Business Media.
- Kuba, M., & Panholzer, A. (2019). A note on harmonic number identities, Stirling series and multiple zeta values. International Journal of Number Theory, 15(7), 1323–1348.
- Loeb, D. E. (1992). A generalization of the Stirling numbers. Discrete Mathematics, 103(3), 259–269.
- Mengoli, P. (1650). Praefatio [Preface]. Novae quadraturae arithmeticae, seu de additione fractionum [New arithmetic quadrature (i.e., integration), or on the addition of fractions]. Bologna: Giacomo Monti.
- Murahara, H., & Ono, M. (2019). Yamamoto’s interpolation of finite multiple zeta and zeta-star values. ArXiv. https://doi.org/10.48550/arXiv.1908.09307 .
- Nielsen, N. (1923). Traité élémentaire des nombres de Bernoulli. Paris, Gauthier-Villars.
- Oresme, N. (1961). Quaestiones super geometriam Euclidis, Vol. 3. Brill Archive.
- Propp, J. (1989). Some variants of Ferrers diagrams. Journal of Combinatorial Theory, Series A, 52(1), 98–128.
- Rademacher, H. (1938). On the partition function p(n). Proceedings of the London Mathematical Society, s2-43(1), 241–254.
- Schneider, R. (2016). Partition zeta functions. Research in Number Theory, 2(1), 9.
- Wang, W., & Wang, T. (2009). General identities on Bell polynomials. Computers & Mathematics with Applications, 58(1), 104–118.
- Xu, C. (2021). Duality Formulas for Arakawa–Kaneko Zeta Values and Related Variants. Bulletin of the Malaysian Mathematical Sciences Society, 44(5), 3001–3018.
- Zagier, D. (1994). Values of zeta functions and their applications. Proceedings of the First European Congress of Mathematics, Paris, July 6–10, 1992, Springer, 497–512.
Manuscript history
- Received: 3 February 2021
- Revised: 25 January 2022
- Accepted: 12 April 2022
- Online First: 18 April 2022
Related papers
Cite this paper
El Haddad, R. (2022). A generalization of multiple zeta values. Part 1: Recurrent sums. Notes on Number Theory and Discrete Mathematics, 28(2), 167-199, DOI: 10.7546/nntdm.2022.28.2.167-199.


