Some equalities and binomial sums about the generalized Fibonacci number un

Yücel Türker Ulutaş and Derya Toy
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 2, Pages 252–260
DOI: 10.7546/nntdm.2022.28.2.252-260
Full paper (PDF, 146 Kb)

Details

Authors and affiliations

Yücel Türker Ulutaş
Department of Mathematics, University of Kocaeli
Kocaeli, Turkey

Derya Toy
Institute of Science and Technology, University of Kocaeli
Kocaeli, Turkey

Abstract

In this study, we take the generalized Fibonacci sequence \{u_{n}\} as u_{0}=0,u_{1}=1 and \ u_{n}=ru_{n-1}+u_{n-2} for n>1, where r is a non-zero integer. Based on Halton’s paper in [4], we derive three interrelated functions involving the terms of generalized Fibonacci sequence \{u_{n}\}. Using these three functions we introduce a simple approach to obtain a lot of identities, binomial sums and alternate binomial sums involving the terms of generalized Fibonacci sequence \{u_{n}\}.

Keywords

  • Generalized Fibonacci numbers
  • Sums of generalized Fibonacci numbers
  • Binomial sums

2020 Mathematics Subject Classification

  • 11B37
  • 11B39
  • 11B65

References

  1. Adegoke, K. (2018). Fibonacci and Lucas identities the golden way. arXiv. https://doi.org/10.48550/arXiv.1810.12115.
  2. Bicknell, M. (1975). A primer on the Pell sequences and related sequences. The Fibonacci Quarterly, 13(4), 345–349.
  3. Filipponi, P., & Horadam, A. F. (1993). Second derivative sequences of the Fibonacci and Lucas polynomials. The Fibonacci Quarterly, 31(3), 194–204.
  4. Halton, J. H. (1965). On a general Fibonacci identity. The Fibonacci Quarterly, 3(1), 31–43.
  5. Horadam, A. F. (1965). Basic properties of a certain generalized sequence of number. The Fibonacci Quarterly, 3(3), 161–176.
  6. Horadam, A. F. (1965). Generating functions for powers of a certain generalized sequence of numbers. Duke Mathematical Journal, 32, 437–446.
  7. Kılıç, E., Ömür, N., & Türker Ulutaş, Y., (2009). Matrix representation of the second order recurrence 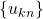\{u_{kn}\}. Ars Combinotaria, 93, 181–190.
  8. Kılıç, E., Ömür, N., & Türker Ulutaş, Y. (2011). Binomial sums whose coefficients are products of terms of binary sequences. Utilitas Mathematica, 84, 45–52.
  9. Kılıç, E., Türker Ulutaş, Y., & Ömür, N. (2012). Formulas for weighted binomial sums with the powers of terms of binary recurrences. Miskolc Mathematical Notes, 13(1), 53–65.
  10. Komatsu, T., & Cook, C. K. (2016). Some identities for sequences of binomial sums of generalized Fibonacci numbers. The Fibonacci Quarterly, 54(2), 105–111.
  11. Koshy, T. (2018). Fibonacci and Lucas Numbers with Applications. A Wiley-Interscience Publication, New York.
  12. Layman, J. W. (1977). Certain general binomial-Fibonacci sums. The Fibonacci Quarterly, 15(4), 362–366.
  13. Seibert, J., & Trojovsky, P. (2006). On sums of certain products of Lucas numbers. The Fibonacci Quarterly, 44(2), 172–180.
  14. Soykan, Y. (2020). Generalized Fibonacci numbers: Sum formulas. Journal of Advances in Mathematics and Computer Science, 35(1), 89–104.

Manuscript history

  • Received: 4 June 2021
  • Revised: 28 April 2022
  • Accepted: 5 May 2022
  • Online First: 6 May 2022

Related papers

Cite this paper

Türker Ulutaş, Y., & Toy, D. (2022). Some equalities and binomial sums about the generalized Fibonacci number un. Notes on Number Theory and Discrete Mathematics, 28(2), 252-260, DOI: 10.7546/nntdm.2022.28.2.252-260.

Comments are closed.