Volume 24 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
Happy φ(164)-th birthday, Prof. Tony Shannon!
Editorial. Pages 1–2
Krassimir T. Atanassov and József Sándor
Editorial (PDF, 250 Kb)
On a new arithmetic function
Original research paper. Pages 3–10
Krassimir T. Atanassov and József Sándor
Full paper (PDF, 177 Kb) | Abstract
A new arithmetic function is introduced and its basic properties are studied. Some inequalities between the new and some other arithmetic functions are formulated and proved.
An identical equation for arithmetic functions of several variables and applications
Original research paper. Pages 11–17
Vichian Laohakosol and Pinthira Tangsupphathawat
Full paper (PDF, 180 Kb) | Abstract
An identical equation for arithmetic functions is proved generalizing the 2-variable case due to Venkataraman. It is then applied to characterize multiplicative functions which are variable-separated, and to deduce interesting properties of generalized Ramanujan sums.
Revisiting some old results on odd perfect numbers
Original research paper. Pages 18–25
Jose Arnaldo Bebita Dris and Doli-Jane Uvales Tejada
Full paper (PDF, 177 Kb) | Abstract
In this note, we revisit and show how some old results on odd perfect numbers follow from assuming some unproven yet reasonable conjectures.
The Redheffer numbers and their applications
Original research paper. Pages 26–37
Ömür Deveci and Anthony G. Shannon
Full paper (PDF, 142 Kb) | Abstract
In this paper, we define the Redheffer numbers and then we obtain their miscellaneous properties. Also, we study the Redheffer numbers modulo m. Furthermore, we define the Redheffer orbits and the basic Redheffer orbits of 2-generator and 3-generator groups, then we examine the lengths of the periods of these orbits. Finally, we obtain the Redheffer lengths and the basic Redheffer lengths of some special finite groups as applications of Redheffer orbits and the basic Redheffer orbits.
Results on generalized negabent functions
Original research paper. Pages 38–44
Rashmeet Kaur and Deepmala Sharma
Full paper (PDF, 166 Kb) | Abstract
In this article, we characterize generalized negabent functions on ℤ2n with values in ℤ8 and ℤ16. Furthermore, we propose several constructions of generalized negabent functions.
A new symmetric endomorphism operator for some generalizations of certain generating functions
Original research paper. Pages 45–58
Ali Boussayoud, Abdelhamid Abderrezzak and Serkan Araci
Full paper (PDF, 207 Kb) | Abstract
In this article, we introduce new symmetric endomorphism operators by making use of appropriate infinite product series. The main results show that after direct calculations, the proposed operators are qualified to obtain generating functions for k-Jacobsthal numbers and Tchebychev polynomials of the first and second kind.
Simple applications of continued fractions and an elementary result on Heron’s algorithm
Original research paper. Pages 59–69
Antonino Leonardis
Full paper (PDF, 904 Kb) | Abstract
The paper is a continuation of the author’s previous works on continued fractions, and has been presented at the AMS special session on Continued Fraction during the Joint Mathematical Meetings 2017, Atlanta GA. The first part is more introductory/educational, explaining the importance of matricial and Diophantine methods in the topic of continued fractions. We will begin this part discussing geometrical illusions which can arise from properties of continued fractions and associated matrices, proving thoroughly the mathematical reasons of this fact. After this, we will deal with the Pythagorean problem of the right-angled isosceles triangles finding all solutions to the simple Diophantine equation l2 + (l + 1)2 = d2, which will give a “Pseudo-Pythagorean” triangle. In the second part, recalling all the methods introduced in the first one, we will prove a theorem (the main result), which relates continued fractions with Heron’s algorithm, giving some examples. This theorem is proved in a complete form, which considers all possibilities and its vice-versa, unlike all other minor results that can be found in the literature (see [2,3]).
Generalized dual Fibonacci quaternions with dual coefficient
Original research paper. Pages 70–85
Fügen Torunbalcı Aydın
Full paper (PDF, 226 Kb) | Abstract
In this paper, we defined the generalized dual Fibonacci quaternions with dual coefficient. Also, we investigated the relations between the generalized dual Fibonacci quaternions with dual coefficient. Furthermore, we gave the Binet’s formulas and Cassini identities for these quaternions.
The structure of prime sums
Original research paper. Pages 86–91
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 114 Kb) | Abstract
The development of prime sequences has allowed the detailed structure of prime sums to be made. Such structures help to explain why some sums yield primes while others give composites. The application of right-end-digit (modulo 10) structure permits analysis independent of the size of the integers being examined.
Some combinatorial identities via Stirling transform
Original research paper. Pages 92–98
Fouad Bounebirat, Diffalah Laissaoui and Mourad Rahmani
Full paper (PDF, 191 Kb) | Abstract
The aim of this paper is to present some results on the use of the generalized Stirling transform. First, we establish a generalization of a recent Guo–Qi’s identity for Bell numbers. Finally, a new explicit formula for Euler numbers are given.
Explicit expression for symmetric identities of w-Catalan–Daehee polynomials
Original research paper. Pages 99–111
Taekyun Kim, Seog-Hoon Rim, Dmitry V. Dolgy and Sung-Soo Pyo
Full paper (PDF, 209 Kb) | Abstract
Recently, Catalan–Daehee numbers are studied by several authors. In this paper, we consider the w-Catalan–Daehee polynomials and investigate some properties for those polynomials. In addition, we give explicit expression for the symmetric identities of the w-Catalan–Daehee polynomials which are derived from p-adic invariant integral on ℤp.
On the Diophantine equation Ln − Lm = 3 • 2a
Original research paper. Pages 112–119
Zafer Şiar and Refik Keskin
Full paper (PDF, 191 Kb) | Abstract
In this paper, we solve Diophantine equation in the tittle in positive integers m, n and a. It is shown that solutions of the equation Ln − Lm = 3 • 2a are given by L11 − L4 = 199 − 7 = 3 • 26, L4 − L3 = 7 − 4 = 3 • 20, L4 − L1 = 7 − 1 = 3 • 2, L3 − L1 = 4 − 1 = 3 • 20. In order to prove our result, we use lower bounds for linear forms in logarithms and a version of the Baker–Davenport reduction method in Diophantine approximation.
On the convergence of second-order recurrence series
Original research paper. Pages 120–127
Bijan Kumar Patel and Prasanta Kumar Ray
Full paper (PDF, 150 Kb) | Abstract
In this article, a generalized second-order linear recurrence sequence is considered and the range of the convergence of this sequence with power series is studied. An estimation for the speed of convergence of the second-order linear recurrence series is also given.
Valuations, arithmetic progressions, and prime numbers
Original research paper. Pages 128–132
Shin-ichiro Seki
Full paper (PDF, 156 Kb) | Abstract
In this short note, we give two proofs of the infinitude of primes via valuation theory and give a new proof of the divergence of the sum of prime reciprocals by Roth’s theorem and Euler–Legendre’s Theorem for arithmetic progressions.
Canonical matrices with entries integers modulo p
Original research paper. Pages 133–143
Krasimir Yordzhev
Full paper (PDF, 173 Kb) | Abstract
The work considers an equivalence relation in the set of all
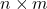
matrices with entries in the set
![Rendered by QuickLaTeX.com [p] = \{0, 1, ..., p-1\}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-3f58bf0c870c8b46dcab1fcdd1bad076_l3.png)
. In each element of the factor-set generated by this relation, we define the concept of canonical matrix, namely the minimal element with respect to the lexicographic order. We have found a necessary and sufficient condition for an arbitrary matrix with entries in the set
![Rendered by QuickLaTeX.com [p]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-84a6b6c7f19b5ab0aa021ddedd1bd2e4_l3.png)
to be canonical. For this purpose, the matrices are uniquely represented by ordered

-tuples of integers.
Extremal chemical trees of the first reverse Zagreb beta index
Original research paper. Pages 144–148
Süleyman Ediz and Mesut Semiz
Full paper (PDF, 133 Kb) | Abstract
The reverse vertex degree of a vertex v of a simple connected graph G defined as cv = Δ − dv + 1, where Δ denotes the largest of all degrees of vertices of G and dv denotes the number of edges incident to v. The first reverse Zagreb beta index of a simple connected graph G defined as CMβ1(G) = Σuv∈E(G)(cu + cv). In this paper, we characterized maximum chemical trees with respect to the first reverse Zagreb beta index.
Editorial note
Pages 149–150
Editorial (PDF, 35 Kb)
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. DNP-06-38/2017.
Volume 24 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


