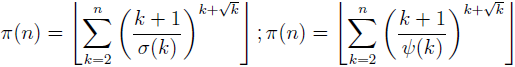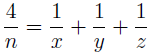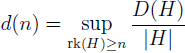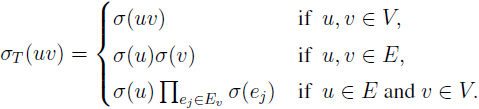Volume 19, 2013, Number 3

Volume 19 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Professor Anthony Shannon at F4 × F5 × F5 years
Editorial. Pages 1–4
Krassimir T. Atanassov
Editorial (PDF, 84 Kb)

The Pascal–Fibonacci numbers
Original research paper. Pages 5–11
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 144 Kb) | Abstract

The Pascal–Fibonacci (PF) numbers for a given Fibonacci number sum to give the values of that Fibonacci number. Individual PF numbers are members of one of the triangular, tetrahedral or pentagonal series or have factors in common with the pyramidal or other geometric series. For composite numbers, partial sums of PF numbers can yield a factor, while prime Fibonacci numbers are detected with sums of squares.

Pulsating Fibonacci sequence
Original research paper. Pages 12–14
Krassimir T. Atanassov
Full paper (PDF, 100 Kb) | Abstract

A new type Fibonacci sequence is introduced and explicit formulas for the form of its members is formulated and proved.

A note on modified Jacobsthal and Jacobsthal–Lucas numbers
Original research paper. Pages 15–20
Julius Fergy T. Rabago
Full paper (PDF, 144 Kb) | Abstract

In this note, some relations between Jacobsthal and Jacobsthal–Lucas numbers and their respective modifications due to K. T. Atanassov {1, 2} and Y. Shang {4} are presented.

Relations on Jacobsthal numbers
Original research paper. Pages 21–23
S. Arunkumar, V. Kannan and R. Srikanth
Full paper (PDF, 120 Kb) | Abstract

Relations between Jacobsthal numbers, prime Jacobsthal numbers and Fibonacci Jacobsthal numbers are found out.

New explicit representations for the prime counting function
Original research paper. Pages 24–27
Mladen Vassilev-Missana
Full paper (PDF, 148 Kb) | Abstract

In the paper the new formulae for the prime counting function π:
\pi(n)= \left\lfloor \sum_{k=2}^n \left(\frac{k+1}{\sigma(k)}\right)^{k+\sqrt{k}} \right\rfloor; \pi(n)= \left\lfloor \sum_{k=2}^n \left( \frac{k+1}{\psi(k)} \right)^{k+\sqrt{k}}\right\rfloor
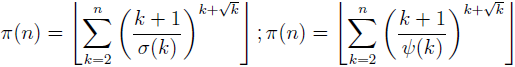
(where σ is the sum-of-divisor function and ψ is the Dedekind’s function) are proposed and proved. Also a general theorem (Theorem 1) is obtained that gives infinitely many explicit formulae for the prime counting function π (depending on arbitrary arithmetic function with strictly positive values, satisfying certain condition).

On the area and volume of a certain regular solid and the Diophantine equation 1/2 = 1/x + 1/y + 1/z
Original research paper. Pages 28–32
Julius Fergy T. Rabago and Richard P. Tagle
Full paper (PDF, 147 Kb) | Abstract

In this paper, we study some elementary problems involving surface area and volume of a certain regular solid. In particular, we find integral dimensions of a rectangular prism in which its surface area and volume are numerically equal. The problem leads us in solving a specific case of the well-known Diophantine problem
\frac{4}{n}=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}

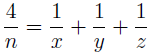
BBP-type formulas, in general bases, for arctangents of real numbers
Original research paper. Pages 33–54
Kunle Adegoke and Olawanle Layeni
Full paper (PDF, 221 Kb) | Abstract

BBP-type formulas are usually discovered experimentally, one at a time and in specific bases, through computer searches using PSLQ or other integer relations finding algorithms. In this paper, however, we give a systematic analytical derivation of numerous new explicit digit extraction BBP-type formulas for the arctangents of real numbers in general bases. Our method has the clear advantage that the proofs of the formulas are contained in the derivations, whereas in the experimental approach, proofs of discovered formulas have to be found separately. The high point of this paper is perhaps the discovery, for the first time, of a BBP-type formula for \pi \sqrt{5}.

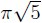
On subsets of finite Abelian groups without non-trivial solutions of x1 + x2 + … + xs – sxs+1 = 0
Original research paper. Pages 55–59
Ran Ji and Craig V. Spencer
Full paper (PDF, 202 Kb) | Abstract

Let D(G) be the maximal cardinality of a set A ⊆ G that contains no non-trivial solution to x1 + … + xs − sxs+1 = 0 with xi ∈ A(1 ≤ i ≤ s + 1). Let
d(n) = \displaystyle\sup_{\rk(H)\geq n} \frac{D(H)}{\vert H \vert}
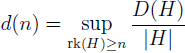
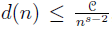
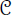
where rk(H) is the rank of H. We prove that for any n ∈ ℕ, d(n) \leq \frac{\Ccc}{n^{s-2}}, where \Ccc is a fixed constant depending only on s.

A note on the modified q-Dedekind sums
Original research paper. Pages 60–65
Serkan Araci, Erdoğan Şen and Mehmet Acikgoz
Full paper (PDF, 184 Kb) | Abstract

In the present paper, the fundamental aim is to consider a p-adic continuous function for an odd prime to inside a p-adic q-analogue of the higher order Extended Dedekind-type sums related to q-Genocchi polynomials with weight α by using fermionic p-adic invariant q-integral on ℤp.

Modular zero divisors of longest exponentiation cycle
Original research paper. Pages 66–69
Amin Witno
Full paper (PDF, 115 Kb) | Abstract

We show that the sequence wk mod n, given that gcd(w, n) > 1, can reach a maximal cycle length of ϕ(n) if and only if n is twice an odd prime power, w is even, and w is a primitive root modulo n=2.

A characterization of canonically consistent total signed graphs
Original research paper. Pages 70–77
Deepa Sinha and Pravin Garg
Full paper (PDF, 164 Kb) | Abstract

The canonical marking on a signed graph (or sigraph, in short) S is defined as: for each vertex v ∈ V (S), μσ(v) = Πej ∈ Ev, where Ev is the set of edges ej incident at v in S. If S is canonically marked, then a cycle Z in S is said to be canonically consistent (C-consistent) if it contains an even number of negative vertices and the given sigraph S is C-consistent if every cycle in it is C-consistent. The total sigraph T(S) of a sigraph S = (V, E, σ) has T(Se) as its underlying graph and for any edge uv of T(Se),
\sigma_T(uv) = \begin{cases} \sigma(uv) & \text{if \ $u,v \in V,$}\\ \sigma(u)\sigma(v) & \text{if \ $u,v \in E,$}\\ \sigma(u)\prod_{e_j \in E_{v}} \sigma(e_j) & \text{if \ $u \in E \ $and$ \ v \in V.$} \end{cases}
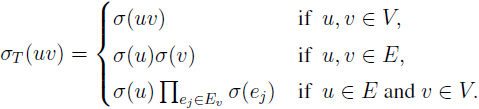
In this paper, we establish a characterization of canonically consistent total sigraphs.

Integer sequences from walks in graphs
Original research paper. Pages 78–84
Ernesto Estrada and José A. de la Peña
Full paper (PDF, 168 Kb) | Abstract

We define numbers of the type Oj(N) = N0 – N1 + N2 – … + N2j and Ej(N) = –N0 + N1 – N2 + … + N2j+1 (j = 0, 1, 2, …) and the corresponding integer sequences. We prove that these integer sequences, e.g., S0(N) = O0(N), O1(N), …, Or(N), … and SE(N) = E0(N), E1(N), …, Er(N), … correspond to the number of odd and even walks in complete graphs KN. We then prove that there is a unique family of graphs which have exactly the same sequence of odd walks between connected nodes and of even walks between pairs of nodes at distance two, respectively. These graphs are the crown graphs: G2n = K2 ⊗ Kn.

Volume 19 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Comments are closed.