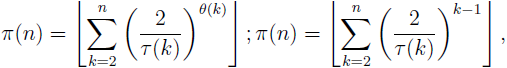Volume 19, 2013, Number 4

We offer an elementary approach to the solution of diophantine equation

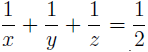
considered recently in Vol. 19, No. 3 of this journal. An extension is provided, too.

The b-parts of real numbers and the generalized division algorithm were considered and discussed in . Also some of their algebraic properties have been studied in . In this paper we continue it and introduce a unique finite representation of real numbers to the base of an arbitrary real number b ≠ 0, ± 1 (namely finite b-representation), by using them. Finally we prove a necessary and sufficient conditions for the finite b-representation to be digital.

An edge uv in a graph G is directionally labeled by an ordered pair ab if the label ℓ(uv) on uv is ab in the direction from u to v; and ℓ(vu) = ba. A (2, d)-sigraph G = (V, E) is a graph in which every edge is directionally labeled by an ordered pair ab ∈ {++, −−, +−, −+}. A (2, d)-sigraph G has a uniform-directional edge labeling (ude-labeling) at a vertex u in G, if for each neighbor v of u, either ℓ(vu) ∈ {++, +−} or ℓ(vu) ∈ {−−, −+}. Further, G is ude-balanced if it has such a labeling at each of its vertex. Two characterizations of ude-balanced (2, d)-sigraphs are obtained. Using a notion of 2-splitting of a (2, d)-sigraphs, we define a 2-balanced (2, d)-sigraph, and obtain a characterization of 2-balanced (2, d)-sigraph which is similar to a characterization of balanced sigraphs. Further, the notion of clusterability of signed graphs is extended to (2, d)-sigraphs, and a characterization of clusterable (2, d)-sigraph is obtained. The notions of ude-balance and clusterability are extended to (n, d)-sigraphs. Some applications of (2, d)-sigraphs are also mentioned.

Rational fractions can often be expressed as the sum of three unit fractions and, generally, such a fraction can be expanded in several ways. An estimate of the maximum number of possible solutions is given. An expression for five possible solutions is given and this is used to obtain several general expansions.

Second type of Pulsated Fibonacci sequence is introduced and explicit formulas for the form of its members are formulated and proved.

In this paper we define T*T multiplicative divisors function. This notion leads us to generalized multiplicative perfect numbers like T*T perfect numbers, k − T*T perfect numbers and T*₀T−super-perfect numbers. We attempt to characterize these numbers.

A commutative semigroup of abstract factorials is defined in the context of the ring of integers. Given a subset X ⊆ ℤ+, or ℤ, we construct a “factorial set” with which one may define a multitude of abstract factorials on X. These factorial sets are then used to show that given any set X of positive integers we can define infinitely many factorial functions on X each having interesting properties. Such factorials are also studied independently of whether or not there is an association to sets of integers. Using an axiomatic approach we study the possible equality of consecutive factorials, the ratios of consecutive factorials and we provide many examples outlining the applications of the ensuing theory; examples dealing with sets of prime numbers, Fibonacci numbers, and highly composite numbers among other sets of integers. One of the advantages in using this setting is that many apparently independent irrationality criteria involving factorials can be assimilated within this scheme.

In the paper the following explicit formulae for the prime counting function π are proposed and proved:

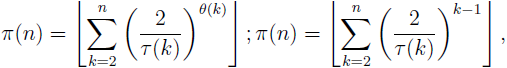
where τ is the number-of-divisors function, θ is either the sum-of-divisors function σ or Dedekind function ψ and ⌊⌋ is the floor function. Also an important general theorem (see Theorem 5) which gives an exact formula (depending on an arbitrary arithmetic function with strictly positive values, satisfying certain condition) for the prime counting function π is formulated and proved. This theorem generalizes all other main results in the paper.

A signed graph (marked graph) is an ordered pair S = (G; σ) (S = (G; μ)), where G = (V, E) is a graph called the underlying graph of S and σ : E → {+, −} (μ : V → {+, −}) is a function. The restricted super line graph of index r of a graph G, denoted by RL_r(G). The vertices of RLr(G) are the r-subsets of E(G) and two vertices P = {p₁, p₂ …, p_r} and Q = {q₁, q₂ …, q_r} are adjacent if there exists exactly one pair of edges, say p_i and q_j , where 1 ≤ i; j ≤ r, that are adjacent edges in G.
Analogously, one can define the restricted super line signed graph of index r of a signed graph S = (G; σ) as a signed graph RLr(S) = (RLr(G); σ′), where RLr(G) is the underlying graph of RLr(S), where for any edge PQ in RLr(S), σ′(PQ) = σ(P)σ(Q). It is shown that for any signed graph S, its RLr(S) is balanced and we offer a structural characterization of restricted super line signed graphs of index r.
Further, we characterize signed graphs S for which RLr(S) ~ Lr(S) and RLr(S) ≅ Lr(S), where ~ and ≅ denote switching equivalence and isomorphism and RLr(S) and Lr(S) are denotes the restricted super line signed graph of index r and super line signed graph of index r of S, respectively.