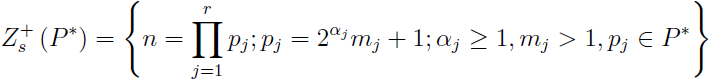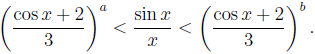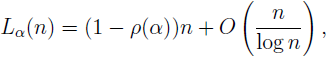Volume 19, 2013, Number 1

Volume 19 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Sum of cubes is square of sum
Original research paper. Pages 1–13
Edward Barbeau and Samer Seraj
Full paper (PDF, 164 Kb) | Abstract

Inspired by the fact that the sum of the cubes of the first n naturals is equal to the square of their sum, we explore, for each n, the Diophantine equation representing all non-trivial sets of n integers with this property. We find definite answers to the standard question of infinitude of the solutions as well as several other surprising results.

On the composition of the functions σ and φ on the set Z_s⁺(P*)
Original research paper. Pages 14–18
Aleksander Grytczuk
Full paper (PDF, 152 Kb) | Abstract

In 1964, A. Mąkowski and A. Schinzel ({8}, Cf.{6}) conjectured that for all positive integers m, we have
$\frac{\sigma \left( \varphi \left( m\right) \right) }{m}\geq \frac{1}{2},$ (*)
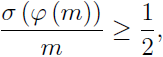
where σ denote the sum of divisors function and φ is the Euler’s totient function.
Let P be the set of all odd primes and
P* = {p ∈ P; p = 2^αk + 1; α ≥ 1; k > 1; (k,2) = 1}.
Moreover, let
$Z_{s}^{+}\left( P^{\ast }\right) =\left\{n=\dprod \limits_{j=1}^{r}p_{j};p_{j}=2^{\alpha _{j}}m_{j}+1;\alpha _{j}\geq 1,m_{j}>1,p_{j}\in P^{\ast }\right\}$
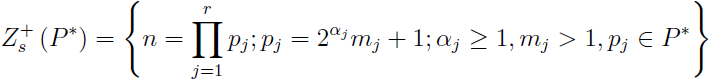
where (m_j, m_k) = 1; for all j ≠ k, j, k = 1, 2, …, r. In this paper we prove that if n ∈ $Z_{s}^{+}\left( P^{\ast }\right)$
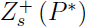
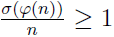
then we have $\frac{\sigma \left( \varphi \left( n\right) \right) }{n}\geq 1$ . From this and Sándor’s result it follows that (*) is true for all positive integers m ≥ 1 such that the squarefree part of m ∈ $Z_{s}^{+}\left( P^{\ast }\right)$ .

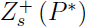
Note on φ and ψ functions
Original research paper. Pages 19–21
V. Kannan and R. Srikanth
Full paper (PDF, 139 Kb) | Abstract

In this paper, we improve the lower bound of the paper {3}.

Note on φ, ψ and σ-functions. Part 6
Original research paper. Pages 22–24
Krassimir T. Atanassov
Full paper (PDF, 118 Kb) | Abstract

The inequality φ(n)ψ(n)σ(n) ≥ n³ + n² − n − 1. connecting φ, ψ and σ-functions is formulated and proved.

Gaussian Jacobsthal and Gaussian Jacobsthal Lucas polynomials
Original research paper. Pages 25–36
Mustafa Asci and Esref Gurel
Full paper (PDF, 164 Kb) | Abstract

In this study we define and study the Gaussian Jacobsthal and Gaussian Jacobsthal Lucas polynomials. We give generating function, Binet formula, explicit formula, Q matrix, determinantal representations and partial derivation of these polynomials. By defining these Gaussian polynomials for special cases GJ_n(1) is the Gaussian Jacobsthal numbers, Gj_n(1) is the Gaussian Jacobsthal Lucas numbers defined in {2}.

On integer solutions of x⁴ + y⁴ – 2z⁴ – 2w⁴ = 0
Original research paper. Pages 37–43
Dustin Moody and Arman Shamsi Zargar
Full paper (PDF, 157 Kb) | Abstract

In this article, we study the quartic Diophantine equation x⁴ + y⁴ – 2z⁴ = 0. We find non-trivial integer solutions. Furthermore, we show that when a solution has been found, a series of other solutions can be derived. We do so using two different techniques. The first is a geometric method due to Richmond, while the second involves elliptic curves.

New explicit formulae for the prime counting function
Original research paper. Pages 44–49
Mladen Vassilev-Missana
Full paper (PDF, 159 Kb) | Abstract

In the paper new explicit formulae for the prime counting function π are proposed and proved. They depend on arbitrary positive arithmetic function which satisfies certain condition. As a particular case a formula for π depending on Euler’s function φ is obtained. To the author’s best knowledge such kind of formulae are proposed for the first time in the mathematical literature.

Sharp Cusa–Huygens and related inequalities
Original research paper. Pages 50–54
József Sándor
Full paper (PDF, 130 Kb) | Abstract

We determine the best positive constants a and b such that
$\left(\ds\f{\cos x+2}{3}\right)^a<\ds\f{\sin x}{x}<\left(\ds\f{\cos x+2}{3}\right)^b.$
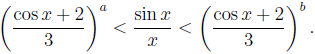
Similar sharp inequalities are also considered.

A note on the density of the Greatest Prime Factor
Original research paper. Pages 55–58
Rafael Jakimczuk
Full paper (PDF, 148 Kb) | Abstract

Let P(n) be the greatest prime factor of a positive integer n ≥ 2. Let L (n) be the number of 2 ≤ k ≤ n such that P(k) > k^α, where 0 < α < 1. We prove the following asymptotic formula
$L_{\alpha}(n)=(1-\rho(\alpha))n+O\left(\frac{n}{\log n}\right),$
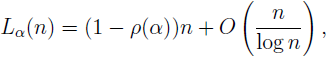
where ρ(α) is the Dickman’s function.

A note on Bernoulli numbers
Original research paper. Pages 59–65
Ramesh Kumar Muthumalai
Full paper (PDF, 139 Kb) | Abstract

Some explicit formulae for Bernoulli numbers and Bernoulli polynomials are derived. Some rational approximations to powers of π are given in terms of Bernoulli numbers.

The structure of the Fibonacci numbers in the modular ring Z₅
Original research paper. Pages 66–72
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 149 Kb) | Abstract

Various Fibonacci number identities are analyzed in terms of their underlying integer structure in the modular ring Z₅.

On new refinements of Kober’s and Jordan’s trigonometric inequalities
Original research paper. Pages 73–83
József Sándor
Full paper (PDF, 174 Kb) | Abstract

This paper deals with some inequalities for trigonometric functions such as the Jordan inequality and Kober’s inequality with refinements. In particular, lower and upper bounds for functions such as (sin x)/x, (1 − cos x)/x and (tan x/2)/x are proved.

Erratum to “Short remark on Jacobsthal numbers”
Erratum. Page 84
Krassimir T. Atanassov
Erratum (PDF, 74 Kb)

Volume 19 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Latest Issue

Journal Contents