Exact formulae for the prime counting function

Mladen Vassilev–Missana
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 4, Pages 77–85
Full paper (PDF, 161 Kb)

Details

Authors and affiliations

Mladen Vassilev–Missana
5 V. Hugo Str, 1124 Sofia, Bulgaria

Abstract

In the paper the following explicit formulae for the prime counting function π are proposed and proved:
\pi(n)=\left \lfloor \sum_{k=2}^n \left(\frac{2}{\tau(k)}\right)^{\theta(k)} \right \rfloor ; \pi(n)=\left \lfloor \sum_{k=2}^n \left(\frac{2}{\tau(k)}\right)^{k-1} \right \rfloor,
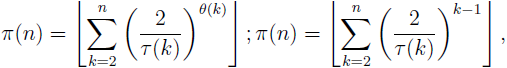
where τ is the number-of-divisors function, θ is either the sum-of-divisors function σ or Dedekind function ψ and ⌊⌋ is the floor function. Also an important general theorem (see Theorem 5) which gives an exact formula (depending on an arbitrary arithmetic function with strictly positive values, satisfying certain condition) for the prime counting function π is formulated and proved. This theorem generalizes all other main results in the paper.

Keywords

  • Prime number
  • Composite number
  • Arithmetic function

AMS Classification

  • 11A25
  • 11A41

References

  1. Sierpiński, W. Elementary Number Theory, 2nd Edition, North Holland, Amsterdam, 1988.
  2. Mitrinović, D., M. Popadić. Inequalities in Number Theory. University of Niš, 1978.

Related papers

Cite this paper

Vassilev–Missana, Mladen (2013). Exact formulae for the prime counting function. Notes on Number Theory and Discrete Mathematics, 19(4), 77-85.

Comments are closed.