New explicit representations for the prime counting function

Mladen Vassilev-Missana
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 3, Pages 24–27
Full paper (PDF, 148 Kb)

Details

Authors and affiliations

Mladen Vassilev-Missana
5 V. Hugo Str., 1124 Sofia, Bulgaria

Abstract

In the paper the new formulae for the prime counting function π:
\pi(n)= \left\lfloor \sum_{k=2}^n \left(\frac{k+1}{\sigma(k)}\right)^{k+\sqrt{k}} \right\rfloor; \pi(n)= \left\lfloor \sum_{k=2}^n \left( \frac{k+1}{\psi(k)} \right)^{k+\sqrt{k}}\right\rfloor
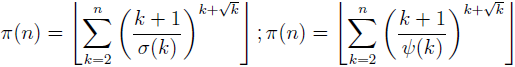
(where σ is the sum-of-divisor function and ψ is the Dedekind’s function) are proposed and proved. Also a general theorem (Theorem 1) is obtained that gives infinitely many explicit formulae for the prime counting function π (depending on arbitrary arithmetic function with strictly positive values, satisfying certain condition).

Keywords

  • Prime number
  • Composite number
  • Arithmetic function

AMS Classification

  • 11A25
  • 11A41

References

  1. Atanassov, K. T. Remark on Jacobsthal numbers, Part 2. Notes on Number Theory and Discrete Mathematics, Vol. 17, 2011, No. 2, 37–39.
  2. Atanassov, K. T. Short remarks on Jacobsthal numbers. Notes on Number Theory and Discrete Mathematics, Vol. 18, 2012, No. 2, 63–64.
  3. Rabago, J. F. T. Circulant Determinant Sequence with Binomial Coefficients, Scientia Magna (on review).
  4. Shang, Y. On the modifications of the Pell–Jacobsthal numbers, Scientia Magna, Vol. 8, 2012, No. 3, 68–70.

Related papers

  1. Shannon, A. G. & Leyendekkers, J. V. (2017). On Legendre’s Conjecture. Notes on Number Theory and Discrete Mathematics, 23(2), 117-125.

Cite this paper

Vassilev-Missana, M. (2013). New explicit representations for the prime counting function. Notes on Number Theory and Discrete Mathematics, 19(3), 24-27.

Comments are closed.