On the area and volume of a certain regular solid and the Diophantine equation 1/2 = 1/x + 1/y + 1/z

Julius Fergy T. Rabago and Richard P. Tagle
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 3, Pages 28–32
Full paper (PDF, 147 Kb)

Details

Authors and affiliations

Julius Fergy T. Rabago
Faculty, Department of Mathematics and Physics
College of Arts and Sciences, Central Luzon State University
Science City of Muñoz 3 120, Nueva Ecija, Philippines

Richard P. Tagle
Faculty, Department of Mathematics and Physics
College of Arts and Sciences, Central Luzon State University
Science City of Muñoz 3 120, Nueva Ecija, Philippines

Abstract

In this paper, we study some elementary problems involving surface area and volume of a certain regular solid. In particular, we find integral dimensions of a rectangular prism in which its surface area and volume are numerically equal. The problem leads us in solving a specific case of the well-known Diophantine problem

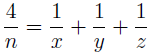
Keywords

• Solids
• Diophantine equation
• Egyptian fraction
• Integral solutions

AMS Classification

• 11D68
• 11A07

References

1. Guy, R. K. Unsolved Problems in Number Theory, 2nd Ed., Springer, Verlag, New York, 1994.
2. Ionascu, E. J., A. Wilson, On the Erdős–Straus Conjecture, Rev. Roumaine Math. Pures Appl., Vol. 56, 2011, No. 1, 21–30.
3. Kishan, H., M. Rani, S. Agarwal, The Diophantine Equations of Second and Higher Degree of the form 3xy = n(x + y) and 3xyz = n(xy + yz + xz) etc, Asian J. of Algebra, Vol. 4, 2011, No. 1, 31–37.
4. Monks, M., A. Velingker. On the Erdős–Straus Conjecture: Properties of Solutions to its Underlying Diophantine Equation (preprint).
5. Zelator, K. An ancient Egyptian problem: The diophantine equation 4/n = 1/x + 1/y + 1/z (preprint).