On subsets of finite Abelian groups without non-trivial solutions of x1 + x2 + … + xs – sxs+1 = 0

Ran Ji and Craig V. Spencer
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 19, 2013, Number 3, Pages 55–59
Full paper (PDF, 202 Kb)

Details

Authors and affiliations

Ran Ji
Department of Mathematics, Wellesley College
106 Central Street, Wellesley, MA 02481, USA

Craig V. Spencer
Department of Mathematics, Kansas State University
138 Cardwell Hall, Manhattan, KS 66506, USA

Abstract

Let D(G) be the maximal cardinality of a set A ⊆ G that contains no non-trivial solution to x1 + … + xs − sxs+1 = 0 with xi ∈ A (1 ≤ i ≤ s + 1). Let
d(n) = \displaystyle\sup_{\rk(H)\geq n} \frac{D(H)}{\vert H \vert}
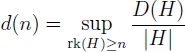
where rk(H) is the rank of H. We prove that for any n ∈ ℕ, d(n) \leq \frac{\Ccc}{n^{s-2}}, where \Ccc is a fixed constant depending only on s.

Keywords

  • Finite Abelian groups
  • Character sums

AMS Classification

  • 11B30
  • 20D60
  • 11T24

References

  1. Lev, V. F. Progression-free sets in finite abelian groups, J. Number Theory Vol. 104, 2004, 162–169.
  2. Liu, Y.-R., C. V. Spencer, A generalization of Meshulam’s Theorem on subsets of finite abelian groups with no 3-term arithmetic progression, Design. Code. Cryptogr., Vol. 52, 2009, 83–91.
  3. Meshulam, R. On subsets of finite abelian groups with no 3-term arithmetic progressions, J. Combin. Theory Ser. A, Vol. 71, 1995, 168–172.
  4. Serre, J.-P. A Course in Arithmetic, Springer-Verlag, New York, 1973.

Related papers

Cite this paper

Ji, R., & Spencer, C. V. (2013). On subsets of finite Abelian groups without non-trivial solutions of x1 + x2 + … + xs – sxs+1 = 0. Notes on Number Theory and Discrete Mathematics, 19(3), 55-59.

Comments are closed.