Volume 24 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4
The system of prime coordinates assigned to the positive integers
Original research paper. Pages 1–5
Silviu Guiasu
Full paper (PDF, 147 Kb) | Abstract
Due to the fundamental theorem of number theory, the positive integers may be represented by vectors whose components are the unique corresponding powers of the prime numbers. Taking the prime numbers as coordinates, to each positive integer we assign a prime vector, whose components are the powers of the prime factors of this integer. The geometry of this system of prime coordinates of the positive integers is discussed. It is shown that the prime components assigned to the sequence of positive integers change in a strictly deterministic way and the parallel generating system is presented. Gödel’s prime vectors assigned to formal logical formulas are analyzed.
The ternary Goldbach problem with prime numbers of a mixed type
Original research paper. Pages 6–20
S. I. Dimitrov
Full paper (PDF, 238 Kb) | Abstract
In the present paper we prove that every sufficiently large odd integer
N can be represented in the form
N =
p1 +
p2 +
p3,
where
p1,
p2,
p3 are primes, such that
p1 =
x2 +
y2 + 1,
p2 =
 nc
nc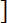
.
Alternative approach to sums of dilates
Original research paper. Pages 21–27
Rafał Bystrzycki and Tomasz Schoen
Full paper (PDF, 186 Kb) | Abstract
We investigate the size of the sets λ1 • A + … + λh • A, where λi are integers. Specifically, we look for upper bounds in terms of the doubling constant K = |A + A|/|A|. We also examine some situations in which those bounds can be significantly strengthened.
A GCD problem and a Hessenberg determinant
Original research paper. Pages 28–31
M. Hariprasad
Full paper (PDF, 151 Kb) | Abstract
In this article we give a proof that, when two integers a and b are coprime ((a, b) = 1, i.e., greatest common divisor (GCD) of a and b is 1), then GCD of a + b and (ap + bp)/(a + b) is either 1 or p for a prime number p. We prove this by linking the problem to a certain type of Hessenberg determinants.
The double Fibonacci sequences in groups and rings
Original research paper. Pages 32–39
Ömür Deveci
Full paper (PDF, 192 Kb) | Abstract
In this paper, we define the double Fibonacci sequence and the basic double Fibonacci sequence in groups and rings. Then we examine these sequences in finite 2-generator groups and rings. Also, we obtain the periods of the double Fibonacci sequences and the basic double Fibonacci sequences in the dihedral group D2m and the ring E for the generating pairs (a, b) and (b, a) as applications of the results obtained.
On the average number of divisors of the sum of digits of squares
Original research paper. Pages 40–46
Teerapat Srichan
Full paper (PDF, 196 Kb) | Abstract
For a positive integer q > 1, we present the estimation of the average number of number of divisors of the sum of digits of squares. Moreover, we extend the result to the sum of digits of the power h, h ≥ 2.
Methods for constructing Collatz numbers
Original research paper. Pages 47–54
Abdullah N. Arslan
Full paper (PDF, 323 Kb) | Abstract
The Collatz conjecture is among the unsolved problems in mathematics. It says that if we take any natural number x; divide it by two if x is even, and multiply it by 3 and add 1 if x is odd; and repeat this rule on the resulting numbers, eventually we obtain 1. For a given positive integer x, we say that x is a Collatz number if the claim of the conjecture is true for x. Computer verification reveals a large range of Collatz numbers. We develop methods by which we construct sets of Collatz numbers.
Quotients of primes in an algebraic number ring
Original research paper. Pages 55–62
Brian D. Sittinger
Full paper (PDF, 191 Kb) | Abstract
It has been established on many occasions that the set of quotients of prime numbers is dense in the set of positive real numbers. More recently, it has been proved that the set of quotients of primes in the Gaussian integers is dense in the complex plane. In this article, we not only extend this result to any imaginary quadratic number ring, but also prove that the set of quotients of primes in any real quadratic number ring is dense in the set of real numbers. To conclude, we show how to extend these results to an arbitrary algebraic number ring.
Structural sequences for primes using right-end-digits
Original research paper. Pages 63–70
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 157 Kb) | Abstract
Integers are expressed in the form nR where R represents the right-end-digits and n represents the digits to the left of R. n can be classified by the sequences {3t}, {3t + 1}, {3t + 2}. When n = 3t + 2, no primes with R = 1 or 7 can be formed with these n; when n = 3t no primes can be formed with R = 3 or 9, but when n = 3t + 1, all REDs can form a prime within the constraints of imbedded sequences.
A note on the Frobenius and the Sylvester numbers
Original research paper. Pages 71–73
Amitabha Tripathi
Full paper (PDF, 138 Kb) | Abstract
Positive integers that cannot be represented by a linear form with relatively prime coefficients and over nonnegative integers are finite in number. We describe a connection between the largest number in this set and the cardinality of this set. We also describe a connection with a subset related to this set.
Global equitable domination in some degree splitting graphs
Original research paper. Pages 74–84
S. K. Vaidya and R. M. Pandit
Full paper (PDF, 250 Kb) | Abstract
A dominating set is called a global dominating set if it is a dominating set of a graph G and its complement G. A subset D of V(G) is called an equitable dominating set if for every v ∈ V(G) − D, there exists a vertex u ∈ D such that uv ∈ E(G) and |dG(u) − dG(v)| ≤ 1. An equitable dominating set D of a graph G is a global equitable dominating set if it is also an equitable dominating set of the complement of G. The minimum cardinality of a global equitable dominating set of G is called the global equitable domination number of G which is denoted by γeg(G). We explore this concept in the context of degree splitting graphs of some graphs.
Relationships between Fibonacci-type sequences and Golden-type ratios
Original research paper. Pages 85–89
R. Patrick Vernon
Full paper (PDF, 158 Kb) | Abstract
The classical Fibonacci sequence is defined so that the first two terms are each equal to 1, and each term after this is the sum of the two terms immediately before it. The golden ratio is the ratio of the longer to shorter side of a rectangle with the property that if we remove a square from the rectangle such that the remainder is also a rectangle, that the old and new rectangles are proportional. Johannes Kepler showed that if we take the sequence of ratios of consecutive Fibonacci numbers, the limit of this sequence is the golden ratio
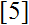
. In this paper, we give a higher dimension extension of Fibonacci sequences and golden ratios and provide a connection between the two.
On two new combined 3-Fibonacci sequences
Original research paper. Pages 90–93
Krassimir T. Atanassov
Full paper (PDF, 118 Kb) | Abstract
Two new combined 3-Fibonacci sequences are introduced and the explicit formulae for their n-th members are given.
Sums of powers of Fibonacci and Lucas numbers: A new bottom-up approach
Original research paper. Pages 94–103
Robert Frontczak
Full paper (PDF, 165 Kb) | Abstract
We derive expressions for sums of first, second, third and fourth powers of Fibonacci and Lucas numbers and their alternating versions. On our way of exploration we rediscover some known results and present new. Focusing on third and fourth order power sums, our findings complete those of Clary and Hemenway, Melham and Adegoke.
On Zudilin-like rational approximations to ζ(5)
Original research paper. Pages 104–116
Anier Soria Lorente
Full paper (PDF, 209 Kb) | Abstract
In this paper we obtain two Zudilin-Like recurrence relations of third order for ζ(5), after applying Zeilberger’s algorithm of creative telescoping to some hypergeometric series. These recurrence relations do not supply diophantine approximations to ζ(5) that prove its irrationality, however it presents an algorithm for fast calculation of this constant. Moreover, we deduce a new continued fraction expansion for ζ(5) as a consequence.
On modular happy numbers
Original research paper. Pages 117–124
Raghib Abusaris and Omar Bayyati
Full paper (PDF, 258 Kb) | Abstract
In this paper, we investigate the asymptotic behavior of the sequences generated by iterating the process of summing the modular powers of the decimal digits of a number. In particular, we identify all modular happy numbers. A number is called modular happy if the sequence obtained by iterating the process of summing the modular powers of the decimal digits of the number ends with 1.
Even dimensional rhotrix
Original research paper. Pages 125–133
A. O. Isere
Full paper (PDF, 207 Kb) | Abstract
A rhotrix is a rhomboidal array of numbers. In many respects, rhotrices are similar to matrices, and matrices, though, are of both even and odd dimensions but only rhotrices of odd dimension are well-known in literature. Even dimensional rhotrix has not been discussed. Therefore, this article introduces rhotrices with even dimension. These rhotrices are a special type of rhotrix where the heart has been extracted. Analysis, examples and some properties of these even-dimensional (heartless) rhotrices are presented and established as algebraic structures, mathematically tractable, and as a contribution to the concept of rhotrix algebra.
On the Iyengar–Madhava Rao–Nanjundiah inequality and its hyperbolic version
Original research paper. Pages 134–139
József Sándor
Full paper (PDF, 155 Kb) | Abstract
We provide a new proof of the trigonometric inequality obtained by K. S. K. Iyengar, B. S. Madhava Rao and T. S. Nanjundiah in 1945, and offer also the hyperbolic version of
this result. Certain related results are pointed out, too.
A symmetric Diophantine equation involving biquadrates
Original research paper. Pages 140–144
Ajai Choudhry
Full paper (PDF, 121 Kb) | Abstract
This paper is concerned with the Diophantine equation
∑i=1n aixi4 = ∑i=1n aiyi4,
where n ≥ 3 and ai, i = 1, 2, …, n, are arbitrary nonzero integers. While a method of obtaining numerical solutions of such an equation has recently been given, it seems that an explicit parametric solution of this Diophantine equation has not yet been published. We obtain a multi-parameter solution of this equation for arbitrary values of ai and for any positive integer n ≥ 3, and deduce specific solutions when n = 3 and n = 4. The numerical solutions thus obtained are much smaller than the integer solutions of such equations obtained earlier.
This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. DNP-06-38/2017.
Volume 24 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4


