Volume 20, 2014, Number 2

Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5

A set of Lucas sequences
Original research paper. Pages 1–5
Krassimir Atanassov
Full paper (PDF, 146 Kb) | Abstract

A new extension of the concept of Fibonacci–like sequences is constructed, related to Lucas sequence. Some of its properties are discussed.

Fibonacci primes
Original research paper. Pages 6–9
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 85 Kb) | Abstract

Fibonacci composites with prime subscripts, Fp, have factors (kp ± 1) in which k is even. The class of p governs the class of k in the modular ring Z5, and the digit sum of p, Fp and a function of Fp provide an approximate check on primality.

Fibonacci primes of special forms
Original research paper. Pages 10–19
Diana Savin
Full paper (PDF, 202 Kb) | Abstract

A study of Fibonacci primes of the form x2 + ry2 (where r = 1; r = prime or r = perfect power) is provided.

(RETRACTED) A Diophantine system about equal sum of cubes
Pages 20–28
Zhi Ren
Retraction Notice
As of 14 April 2016, the paper “A Diophantine system about equal sum of cubes” by Zhi Ren has been retracted and removed from the server!We were notified that an identical version of the paper has been published in the Journal of Integer Sequences, Vol. 16(2013), Article 13.7.8., without the author informing in advance the Editorial Board of the Notes on Number Theory and Discrete Mathematics.The Publisher apologizes for any inconvenience caused!

On two Diophantine equations 2A^6 + B^6 = 2C^6 \pm D^3
Original research paper. Pages 29–34
Susil Kumar Jena
Full paper (PDF, 138 Kb) | Abstract

We give parametric solutions, and thus show that the two Diophantine equations 2A^6 + B^6 = 2C^6 \pm D^3 have infinitely many nontrivial and primitive solutions in positive integers (A, B, C, D).

An explicit estimate for the Barban and Vehov weights
Original research paper. Pages 35–43
Djamel Berkane
Full paper (PDF, 164 Kb) | Abstract

We show that

    \[\sum_{1 \le n \le N} \Bigg ( \sum_{d|n} \lambda_d \Bigg )^2 / n <\!\!< \dfrac{\log N}{\log z},\]

where \lambda_{d} is a real valued arithmetic function called the Barban and Vehov weight and we give an explicit version of a Theorem of Barban and Vehov which has applications to zero-density theorems.

Mean values of the error term with shifted arguments in the circle problem
Original research paper. Pages 44–51
Jun Furuya and Yoshio Tanigawa
Full paper (PDF, 196 Kb) | Abstract

In this paper, we show the relation between the shifted sum of a number-theoretic error term and its continuous mean (integral). We shall obtain a certain expression of the shifted sum as a linear combination of the continuous mean with the Bernoulli polynomials as their coefficients. As an application of our theorem, we give better approximations of the continuous mean by a shifted sum.

On certain inequalities for σ, φ, ψ and related functions
Original research paper. Pages 52–60
József Sándor
Full paper (PDF, 162 Kb) | Abstract

Some new inequalities for the arithmetic functions of the title are considered. Among others we offer a refinement of a recent arithmetic inequality by K. T. Atanassov [1].

On rational fractions not expressible as a sum of three unit fractions
Original research paper. Pages 61–64
Simon Brown
Full paper (PDF, 80 Kb) | Abstract

Of those fractions (a/b < 1) that can not be expressed as a sum of three unit fractions, many can be written in terms of three unit fractions if the smallest denominator is \lfloor b / a \rfloor and the next largest denominator is < 0. General expressions are given for some specific classes of these. Two examples of Yamamoto are reconsidered.

A note on a broken Dirichlet convolution
Original research paper. Pages 65–73
Emil Daniel Schwab and Barnabás Bede
Full paper (PDF, 185 Kb) | Abstract

The paper deals with a broken Dirichlet convolution ⊗ which is based on using the odd divisors of integers. In addition to presenting characterizations of ⊗-multiplicative functions we also show an analogue of Menon’s identity:
\sum\limits_{\stackrel{a\ (mod\ n)}{(a,n)_{\otimes}=1}}{(a-1,n)}=\phi_{\otimes}(n)\left\tau(n)-\frac{1}{2}\tau_{2}(n)\right
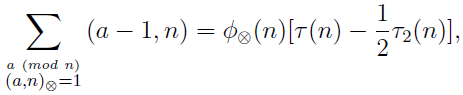
where (a, n)⊗ denotes the greatest common odd divisor of a and n, φ⊗(n) is the number of integers a (mod n) such that (a, n)⊗ = 1, τ(n) is the number of divisors of n, and τ2(n) is the number of even divisors of n.

On a recurrence related to 321–avoiding permutations
Original research paper. Pages 74–78
Toufik Mansour and Mark Shattuck
Full paper (PDF, 166 Kb) | Abstract

Dokos et al. recently conjectured that the distribution polynomial f_n(q) on the set of permutations of size n avoiding the pattern 321 for the number of inversions is given by:

    \[f_n(q) = f_{n-1}(q) + \sum_{k=0}^{n-2} q^{k+1} f_k(q) f_{n-1-k}(q), \quad n \ge 1,\]

with f_0(q) = 1, which was later proven in the affirmative, see [1]. In this note, we provide a new proof of this conjecture, based on the scanning-elements algorithm described in [3], and present an identity obtained by equating two explicit formulas for the generating function \sum_{n \ge 0} a_n(q)x^n.

Nesterenko-like rational function, useful to prove the Apéry’s theorem
Original research paper. Pages 79–91
Anier Soria Lorente
Full paper (PDF, 209 Kb) | Abstract

In this paper, a brief introduction to the Apéry’s result and to the so called phenomenon of Apéry’s is given. Here, a modification of the Nesterenko’s rational function, from which new Diophantine approximations to ζ(3) are deduced, is presented. Moreover, as a consequence we deduce the corresponding Apéry-Like recurrence relation as well as a new continued fraction expansion and a new series expansion for ζ(3).

Some arithmetic properties of an analogue of Möbius function
Original research paper. Pages 92–96
Ramesh Kumar Muthumalai
Full paper (PDF, 141 Kb) | Abstract

Some properties and applications of an analogue of Möbius function are studied in the paper titled, “Some properties and application of a new arithmetic function in analytic number theory”. In this paper, some additional properties of this new arithmetic function connecting with familiar arithmetic functions such as Möbius function, Euler totient function, etc., are given.

Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5

Comments are closed.