József Sándor
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 20, 2014, Number 2, Pages 52–60
Full paper (PDF, 162 Kb)
Details
Authors and affiliations
József Sándor ![]()
Babeș-Bolyai University, Department of Mathematics
Str. Kogălniceanu nr. 1, 400084 Cluj-Napoca, Romania
Abstract
Some new inequalities for the arithmetic functions of the title are considered. Among others we offer a refinement of a recent arithmetic inequality by K. T. Atanassov [1].
Keywords
- Arithmetic functions
- Inequalities for arithmetic functions
- Inequalities of Weierstrass type
AMS Classification
- 11A25
- 26D99
References
- Atanassov, K. T. Note on φ, ψ and σ-functions. Part 6. Notes Numb. Th. Discr. Math., Vol. 19, 2013, No. 1, 22–24.
- Sándor, J., L. Tóth. On certain number-theoretic inequalities. Fib. Quart., Vol. 28, 1990, 255–258.
- Sándor, J., D. S. Mitrinović, B. Crstici, Handbook of number theory I, Springer Verlag, 2006 (first edition by Kluwer, 1995).
- Sándor, J. On certain inequalities for arithmetic functions. Notes Numb. Theor. Discr. Math., Vol. 1, 1995, No. 1, 27–32.
- Sándor, J. On inequalities
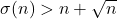 and
and ![Rendered by QuickLaTeX.com \sigma(n) > n + \sqrt{n} + \sqrt[3]{n}](https://nntdm.net/wp-content/ql-cache/quicklatex.com-1ab962d9478666a2ff232c225cceba8c_l3.png) . Octogon Math. Mag., Vol. 16, 2008, No. 1, 276–278.
. Octogon Math. Mag., Vol. 16, 2008, No. 1, 276–278. - Sándor, J. On the inequality
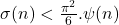 . Octogon Math. Mag., Vol. 16, 2008, No. 1, 295–296.
. Octogon Math. Mag., Vol. 16, 2008, No. 1, 295–296.
Related papers
- Atanassov, K. T. (2013). Note on φ, ψ and σ-functions. Part 6. Notes on Number Theory and Discrete Mathematics, 19(1), 22-24.
- Sándor, J. (2020). On the equation φ(n) + d(n) = n and related inequalities. Notes on Number Theory and Discrete Mathematics, 26(3), 1-4.
- Dimitrov, S. (2023). Lower bounds on expressions dependent on functions φ(n), ψ(n) and σ(n). Notes on Number Theory and Discrete Mathematics, 29(4), 713-716.
- Dimitrov, S. (2024). Lower bounds on expressions dependent on functions φ(n), ψ(n) and σ(n), II. Notes on Number Theory and Discrete Mathematics, 30(3), 547-556.
Cite this paper
Sándor, J. (2014). On certain inequalities for σ, φ, ψ and related functions. Notes on Number Theory and Discrete Mathematics, 20(2), 52-60.


