Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5
Preface
Editorial
Editorial (PDF, 64 Kb)
A note on the Diophantine equations x1k + x2k + x3k + x4k = 2y1k + 2y2k , k = 3, 6
Original research paper. Pages 1–10
Farzali Izadi, Foad Khoshnam and Arman Shamsi Zargar
Full paper (PDF, 178 Kb) | Abstract
It is shown that infinitely many primitive solutions on the Diophantine equations of the title can be found on employing the theory of elliptic curves, which makes it possible to naturally find larger solutions in a matter of minutes.
A note on certain inequalities for bivariate means
Original research paper. Pages 11–13
József Sándor
Full paper (PDF, 123 Kb) | Abstract
We obtain simple proofs of certain results from paper
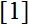
.
The four roots lemma
Original research paper. Pages 14–19
Kristijan Tabak
Full paper (PDF, 172 Kb) | Abstract
Using pairwise abbreviation and simple characterization of zero-sums over
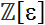
; where ε is root of unity of order 2
n, we manage to prove that a norm of a sum of any four mutually different roots has to be different that 2.
On integer solutions of A5 + B3 = C5 + D3
Original research paper. Pages 20–24
Farzali Izadi and Arman Shamsi Zargar
Full paper (PDF, 154 Kb) | Abstract
In this note, we study the diagonal nonhomogeneous symmetric Diophantine equation of the title, and show that when a solution has been found, a series of other solutions can be derived. This shows that difference of quintics equals difference of cubics for infinitely many integers. We do so using a method involving elliptic curves, which makes it possible to naturally find any solution in a matter of minutes.
On upper Hermite–Hadamard inequalities for geometric-convex and log-convex functions
Original research paper. Pages 25–30
József Sándor
Full paper (PDF, 142 Kb) | Abstract
We offer connections between upper Hermite–Hadarmard type inequalities for geometric convex and logarithmically convex functions.
Extensions to the Zeckendorf Triangle
Original research paper. Pages 31–34
A. G. Shannon and J. V. Leyendekkers
Full paper (PDF, 83 Kb) | Abstract
This note extends some of the characteristics of a Zeckendorf triangle composed of Fibonacci number multiples of the Fibonacci sequence.
A combinatorial proof of multiple angle formulas involving Fibonacci and Lucas numbers
Original research paper. Pages 35–39
Fernando Córes and Diego Marques
Full paper (PDF, 137 Kb) | Abstract
Let
Fn and
Ln be the
n-th Fibonacci and Lucas number, respectively. In this note, we give a combinatorial proof for the following identity
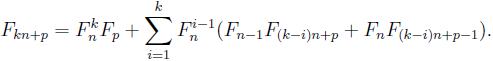
Conjectured polynomial time primality tests for numbers of special forms
Original research paper. Pages 40–43
Predrag Terzić
Full paper (PDF, 145 Kb) | Abstract
Conjectured polynomial time primality tests for numbers of special forms similar to the Riesel primality test for numbers of the form k · 2n − 1 are introduced.
Three identities concerning Fibonacci and Lucas numbers
Original research paper. Pages 44–48
Refik Keskin
Full paper (PDF, 140 Kb) | Abstract
In the literature, there are many identities about Fibonacci and Lucas numbers. In this study, we give three identities concerning Fibonacci and Lucas numbers. Then we present some Diophantine equations such as z2 + x2 + y2 = xyz + 4.
On the local and global principle for system of binary rational cubic forms
Original research paper. Pages 49–57
Lan Nguyen
Full paper (PDF, 141 Kb) | Abstract
It is known that any binary rational cubic form satisfies the Hasse principle. The next natural question to ask is whether this still holds for a system of binary rational cubic forms. However, there seems to be no known result on this topic. In our paper we show, by establishing an explicit equivalence between a rational cubic form and an intersection of quadric surfaces, that any system of finitely many binary rational cubic forms satisfies the Hasse principle.
On some Pascal’s like triangles. Part 7
Original research paper. Pages 58–63
Krassimir T. Atanassov
Full paper (PDF, 159 Kb) | Abstract
A series of Pascal’s like triangles with different forms are described and some of their properties are given.
Identities involving q-Genocchi numbers and polynomials
Original research paper. Pages 64–74
Serkan Aracı, Mehmet Acikgoz, Hassan Jolany and Yuan He
Full paper (PDF, 189 Kb) | Abstract
In this paper, we focus on the q-Genocchi numbers and polynomials. We introduce new identities of the q-Genocchi numbers and polynomials by using the fermionic p-adic integral on ℤp. Also, we give Cauchy-integral formula for the q-Genocchi polynomials and derive the distribution formula q-Genocchi polynomials by using measure theory on p-adic integral. Finally, we get q-Zeta-type function by using Mellin transformation (sometimes known as Laplace transformation) and show that this function interpolates to the q-Genocchi polynomials at negative integers.
Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5