Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5
On two new means of two variables
Original research paper. Pages 1–9
József Sándor
Full paper (PDF, 168 Kb) | Abstract
Let A, G and L denote the arithmetic, geometric resp. logarithmic means of two positive number, and let P denote the Seiffert mean. We study the properties of two new means X resp. Y , defined by X = A · eG / P−1 and Y = G · eL /A − 1.
Calculating terms of associated polynomials of Perrin and Cordonnier numbers
Original research paper. Pages 10–18
Kenan Kaygısız and Adem Şahin
Full paper (PDF, 150 Kb) | Abstract
In this paper, we calculate terms of associated polynomials of Perrin and Cordonnier numbers by using determinants and permanents of various Hessenberg matrices. Since these polynomials are general forms of Perrin and Cordonnier numbers, our results are valid for the Perrin and Cordonnier numbers.
Arithmetical sequences for the exponents of composite Mersenne numbers
Original research paper. Pages 19–26
Simon Davis
Full paper (PDF, 169 Kb) | Abstract
Arithmetical sequences for the exponents of composite Mersenne numbers are obtained from partitions into consecutive integers, and congruence relations for products of two Mersenne numbers suggest the existence of infinitely many composite integers of the form 2p − 1 with p prime. A lower probability for the occurrence of composite Mersenne numbers in arithmetical sequences is given.
The decimal string of the golden ratio
Original research paper. Pages 27–31
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 147 Kb) | Abstract
The decimal expansion of the Golden Ratio is examined through the use of various properties of the Fibonacci numbers and some exponential functions.
n-Pulsated Fibonacci sequence
Original research paper. Pages 32–35
Krassimir Atanassov
Full paper (PDF, 120 Kb) | Abstract
A new type of Fibonacci sequence is introduced and explicit formulas for the form of its members are formulated and proved. It is an extension of the special Fibonacci sequence, introduced in
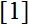
and called a Pulsated Fibonacci sequence.
New modular relations for the Rogers–Ramanujan type functions of order fifteen
Original research paper. Pages 36–48
Chandrashekar Adiga and A. Vanitha
Full paper (PDF, 195 Kb) | Abstract
In this paper, we establish two modular relations for the Rogers–Ramanujan–Slater functions of order fifteen. These relations are analogues to Ramanujan’s famous forty identities for the Rogers–Ramanujan functions.
Furthermore, we give interesting partition theoretic interpretations of these relations.
Balancing sequences of matrices with application to algebra of balancing numbers
Original research paper. Pages 49–58
Prasanta Kumar Ray
Full paper (PDF, 158 Kb) | Abstract
It is well known that, the problem of finding a sequence of real numbers an, n = 0, 1, 2, …, which is both geometric (an + 1 = kan; n = 0, 1, 2, …) and balancing (an + 1 = 6an − an − 1, a0 = 0, a1 = 1) admits an unique solution. In fact, the sequence is 1, λ1, λ12, …, λ1n, … where λ1 = 3 + √8 satisfies the balancing equation λ2 − 6λ + 1. In this paper, we pose an equivalent problem for a sequence of real, nonsingular matrices of order two and show that, this problem admits an infinity of solutions, that is there exist infinitely many such sequences.
The rectangular spiral or the n1 × n2 × … × nk Points Problem
Original research paper. Pages 59–71
Marco Ripà
Full paper (PDF, 589 Kb) | Abstract
A generalization of Ripà’s square spiral solution for the n × n × … × n Points Upper Bound Problem. Additionally, we provide a non-trivial lower bound for the k-dimensional n1 × n2 × … × nk Points Problem. In this way, we can build a range in which, with certainty, all the best possible solutions to the problem we are considering will fall. Finally, we provide a few characteristic numerical examples in order to appreciate the fineness of the result arising from the particular approach we have chosen.
The Fibonacci sequence and the golden ratio in music
Original research paper. Pages 72–77
Robert van Gend
Full paper (PDF, 414 Kb) | Abstract
This paper presents an original composition based on Fibonacci numbers, to explore the inherent aesthetic appeal of the Fibonacci sequence. It also notes the use of the golden ratio in certain musical works by Debussy and in the proportions of violins created by Stradivarius.
Number Theory: A Historical Approach
Book review. Page 78
A. G. Shannon
Book review (PDF, 44 Kb)
Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5


