Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5
On two new means of two variables II
Original research paper. Pages 1–10
József Sándor and Barkat Ali Bhayo
Full paper (PDF, 178 Kb) | Abstract
Here authors establish the inequalities for two means X and Y studied in
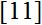
, and give the series expansion of these means.
Frobenius pseudoprimes and a cubic primality test
Original research paper. Pages 11–20
Catherine A. Buell and Eric W. Kimball
Full paper (PDF, 172 Kb) | Abstract
An integer, n, is called a Frobenius probable prime with respect to a polynomial when it passes the Frobenius probable prime test. Composite integers that are Frobenius probable primes are called Frobenius pseudoprimes. Jon Grantham developed and analyzed a Frobenius probable prime test with quadratic polynomials. Using the Chinese Remainder Theorem and Frobenius automorphisms, we were able to extend Grantham’s results to some cubic polynomials. This case is computationally similar but more efficient than the quadratic case.
Generalized Euler–Seidel method for second order recurrence relations
Original research paper. Pages 21–32
M. Cetin Firengiz and A. Dil
Full paper (PDF, 213 Kb) | Abstract
We obtain identities for the generalized second order recurrence relation by using the generalized Euler–Seidel matrix with parameters x, y. As a consequence, we give some properties and generating functions of well-known special integer sequences.
Euler–Euclid’s type proof of the infinitude of primes involving Möbius function
Original research paper. Pages 33–36
Romeo Meštrović
Full paper (PDF, 140 Kb) | Abstract
If we suppose that S = {p1, p2, …, pk} is a set of all primes, then taking x = p1p2…pk + 1 into a formula due to E. Meissel in 1854 gives
(p1 − 1)(p2 − 1)…(pk − 1) = 0.
This obvious contradiction yields the infinitude of primes.
An equation involving Dedekind’s function
Original research paper. Pages 37–39
Cristinel Mortici
Full paper (PDF, 151 Kb) | Abstract
In this note we solve the equation
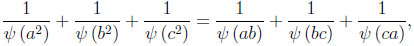
where
ψ is Dedekind’s function.
On some Pascal’s like triangles. Part 6
Original research paper. Pages 40–46
Krassimir T. Atanassov
Full paper (PDF, 125 Kb) | Abstract
A series of Pascal’s like triangles with different forms are described and some of their properties are given.
Fibonacci number sums as prime indicators
Original research paper. Pages 47–52
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 136 Kb) | Abstract
Sums of the first p Fibonacci numbers, Sp, are shown to be related to K in Fp = Kp ± 1, which is itself a useful indicator of primality for Fp. Digit sums of K, Sp, sums of Fp2 and Simson’s identity were compared.
Arithmetic progressions of rectangles on a conic
Original research paper. Pages 53–57
Ajai Choudhry
Full paper (PDF, 113 Kb) | Abstract
In this paper we find infinitely many parabolas on which there exist five points with integer co-ordinates (xj, yj), j = 1, 2, …, 5, such that the products xjyj, j = 1, 2, …, 5, are in arithmetic progression. Similarly, we find infinitely many ellipses and hyperbolas on which there exist six points with integer co-ordinates (xj, yj), j = 1, 2, …, 6, such that the products xjyj, j = 1, 2, …, 6, are in arithmetic progression. Brown had conjectured that there cannot exist four points with integer co-ordinates (xj, yj), j = 1, 2, 3, 4, on a conic such that the four products xjyj, j = 1, 2, 3, 4, are in arithmetic progression. The results of this paper disprove Brown’s conjecture.
Some results about linear recurrence relation homomorphisms
Original research paper. Pages 58–68
Alexandre Laugier and Manjil P. Saikia
Full paper (PDF, 192 Kb) | Abstract
In this paper we propose a definition of a recurrence relation homomorphism and illustrate our definition with a few examples. We then define the period of a k-th order of linear recurrence relation and deduce certain preliminary results associated with them.
Some results on self vertex switching
Original research paper. Pages 69–76
Selvam Avadayappan and M. Bhuvaneshwari
Full paper (PDF, 180 Kb) | Abstract
Let G(V, E) be a graph. A vertex v ∈ V(G) is said to be a self vertex switching of G, if G is isomorphic to Gv, where Gv is the graph obtained from G, by deleting all edges of G incident to v and adding edges between v and the vertices which are not adjacent to v in G. In this paper, we discuss some applications of self vertex switching and list out all trees and unicyclic graphs with unique self vertex switching. We also obtain some more results on self vertex switching.
A note on the greatest common divisor
Original research paper. Pages 77–80
Rafael Jakimczuk
Full paper (PDF, 150 Kb) | Abstract
Let
k ≥ 2 a fixed positive integer. Let
P(
n) be the greatest prime factor of a positive integer
n ≥ 2. Let
Fk(
n) be the number of 2 ≤
s ≤
n such that
P(
s) >
s/k. We prove the following asymptotic formula
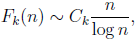
where
Ck is a constant defined in this article.
Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5


