On two Diophantine equations 2A⁶ + B⁶ = 2C⁶ ± D³

Susil Kumar Jena
Notes on Number Theory and Discrete Mathematics, ISSN 1310–5132
Volume 20, 2014, Number 2, Pages 29–34
Full paper (PDF, 138 Kb)

Details

Authors and affiliations

Susil Kumar Jena
Department of Electronics and Telecommunication Engineering
KIIT University
Bhubaneswar 751024, Odisha, India

Abstract

We give parametric solutions, and thus show that the two Diophantine equations 2A⁶ + B⁶ = 2C⁶ ± D³ have infinitely many nontrivial and primitive solutions in positive integers (A, B, C, D).

Keywords

• Diophantine equation
• Diophantine equation 2A⁶ + B⁶ = 2C⁶ + D³
• Diophantine equation 2A⁶ + B⁶ = 2C⁶ − D³
• Equal sums of higher powers

AMS Classification

• 11D41
• 11D72

References

1. Bremner, A. A geometric approach to equal sums of sixth powers, Proc. London Math. Soc., Vol. 43, 1981, 544–581.
2. Brudno, S. On generating infinitely many solutions of the Diophantine equation A⁶ + B⁶ + C⁶ = D⁶ + E⁶ + F⁶, Math. Comp., Vol. 24, 1970, 453–454.
3. Brudno, S. Triples of sixth powers with equal sums, Math. Comp., Vol. 30, 1976, 646–648.
4. Choudhry, A. On equal sums of sixth powers, Indian J. Pure Appl. Math., Vol. 25, 1994, 837–841.
5. Choudhry, A. On equal sums of sixth powers, Rocky Mountain J. Math., Vol. 30, 2000, 843–848.
6. Delorme, J.-J. On the Diophantine equation 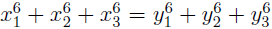, Math. Comput., Vol. 59, 1992, 703–715.