Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5
A set of Lucas sequences
Original research paper. Pages 1–5
Krassimir Atanassov
Full paper (PDF, 146 Kb) | Abstract
Fibonacci primes
Original research paper. Pages 6–9
J. V. Leyendekkers and A. G. Shannon
Full paper (PDF, 85 Kb) | Abstract
Fibonacci primes of special forms
Original research paper. Pages 10–19
Diana Savin
Full paper (PDF, 202 Kb) | Abstract
Pages 20–28
Zhi Ren
Retraction Notice
On two Diophantine equations ![]()
Original research paper. Pages 29–34
Susil Kumar Jena
Full paper (PDF, 138 Kb) | Abstract
An explicit estimate for the Barban and Vehov weights
Original research paper. Pages 35–43
Djamel Berkane
Full paper (PDF, 164 Kb) | Abstract
![Rendered by QuickLaTeX.com \[\sum_{1 \le n \le N} \Bigg ( \sum_{d|n} \lambda_d \Bigg )^2 / n <\!\!< \dfrac{\log N}{\log z},\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-4b89141d611834eb3dd838279bfb3c22_l3.png)
where ![]() is a real valued arithmetic function called the Barban and Vehov weight and we give an explicit version of a Theorem of Barban and Vehov which has applications to zero-density theorems.
is a real valued arithmetic function called the Barban and Vehov weight and we give an explicit version of a Theorem of Barban and Vehov which has applications to zero-density theorems.
Mean values of the error term with shifted arguments in the circle problem
Original research paper. Pages 44–51
Jun Furuya and Yoshio Tanigawa
Full paper (PDF, 196 Kb) | Abstract
On certain inequalities for σ, φ, ψ and related functions
Original research paper. Pages 52–60
József Sándor
Full paper (PDF, 162 Kb) | Abstract
On rational fractions not expressible as a sum of three unit fractions
Original research paper. Pages 61–64
Simon Brown
Full paper (PDF, 80 Kb) | Abstract
A note on a broken Dirichlet convolution
Original research paper. Pages 65–73
Emil Daniel Schwab and Barnabás Bede
Full paper (PDF, 185 Kb) | Abstract
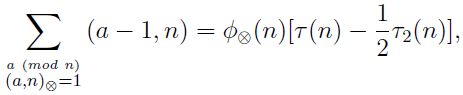
where (a, n)⊗ denotes the greatest common odd divisor of a and n, φ⊗(n) is the number of integers a (mod n) such that (a, n)⊗ = 1, τ(n) is the number of divisors of n, and τ2(n) is the number of even divisors of n.
On a recurrence related to 321–avoiding permutations
Original research paper. Pages 74–78
Toufik Mansour and Mark Shattuck
Full paper (PDF, 166 Kb) | Abstract
![Rendered by QuickLaTeX.com \[f_n(q) = f_{n-1}(q) + \sum_{k=0}^{n-2} q^{k+1} f_k(q) f_{n-1-k}(q), \quad n \ge 1,\]](https://nntdm.net/wp-content/ql-cache/quicklatex.com-a614ec35ad829d72d3c5ef9cb5a0a595_l3.png)
with ![]() , which was later proven in the affirmative, see [1]. In this note, we provide a new proof of this conjecture, based on the scanning-elements algorithm described in [3], and present an identity obtained by equating two explicit formulas for the generating function
, which was later proven in the affirmative, see [1]. In this note, we provide a new proof of this conjecture, based on the scanning-elements algorithm described in [3], and present an identity obtained by equating two explicit formulas for the generating function ![]() .
.
Nesterenko-like rational function, useful to prove the Apéry’s theorem
Original research paper. Pages 79–91
Anier Soria Lorente
Full paper (PDF, 209 Kb) | Abstract
Some arithmetic properties of an analogue of Möbius function
Original research paper. Pages 92–96
Ramesh Kumar Muthumalai
Full paper (PDF, 141 Kb) | Abstract
Volume 20 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4 ▷ Number 5


