Volume 28, 2022, Number 1

Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Character formulas in terms of R_β and R_m functions
Original research paper. Pages 1–8
M. P. Chaudhary, Sangeeta Chaudhary and Kamel Mazhouda
Full paper (PDF, 225 Kb) | Abstract

The authors establish a set of fourteen character formulas in terms of R_β and R_m functions. Folsom [6] studied character formulas and Chaudhary [5] expressed those formulas in terms of continued fraction identities. Andrews et al. [2] introduced multivariate R-functions, which are further classified as R_α; R_β, and R_m (for m = 1, 2, 3, …) functions by Srivastava et al. [10].

On the Vieta–Jacobsthal-like polynomials
Original research paper. Pages 9–19
Wanna Sriprad, Somnuk Srisawat and Kitsana Charoenchaianan
Full paper (PDF, 195 Kb) | Abstract

In this paper, we first introduce the generalization of the Vieta–Jacobsthal polynomial, which is called the Vieta–Jacobsthal-like polynomial. After that, we give the generating function, the Binet formula, and some well-known identities for this polynomial. Finally, we also present the relation between this polynomial and the previously famous Vieta polynomials.

Corrigendum to “On the dimension of an Abelian group” [Notes on Number Theory and Discrete Mathematics, 2022, Volume 27, Number 4, Pages 267–275]
Corrigendum. Page 20
Timo Tossavainen and Pentti Haukkanen
Full paper (PDF, 110 Kb)

Factorials as repdigits in base b
Original research paper. Pages 21–25
Nurettin Irmak and Alain Togbé
Full paper (PDF, 178 Kb) | Abstract

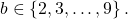
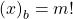
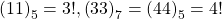
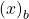
Let $b\in \left\{ 2,3, \ldots,9\right\}.$ In this paper, we show that the solutions of the equation $\left( x\right) _{b}=m!$ are $\left( 11\right) _{5}=3!, \left( 33\right) _{7}=\left( 44\right)_{5}=4!$ , where $\left( x\right) _{b}$ has at least two digits.

Multicomponent hybrid numbers: On algebraic properties and matrix representations of hybrid-hyperbolic numbers
Original research paper. Pages 26–40
Bahar Doğan Yazıcı and Murat Tosun
Full paper (PDF, 222 Kb) | Abstract

In this study, the hybrid-hyperbolic numbers are introduced. This number system is a more general form of the hybrid number system, which is an interesting number system, as well as a number system that includes multicomponent number systems (i.e., complex-hyperbolic, dual-hyperbolic and bihyperbolic numbers). In this paper, we give algebraic properties of hybrid-hyperbolic numbers. In addition, 2 × 2 and 4 × 4 hyperbolic matrix representations of hybrid-hyperbolic numbers are given and some properties of them are examined.

The amplitude of Motzkin paths
Original research paper. Pages 41–47
Helmut Prodinger
Full paper (PDF, 191 Kb) | Abstract

The amplitude of Motzkin paths was recently introduced, which is basically twice the height. We analyze this parameter using generating functions.

Cycles of higher-order Collatz sequences
Original research paper. Pages 48–63
John L. Simons
Full paper (PDF, 326 Kb) | Abstract

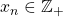
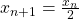
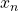
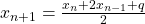
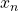
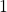
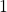
Consider a sequence of numbers $x_n \in \mathbb{Z_+}$ defined by $x_{n+1}= \frac{x_n}{2}$ if $x_n$ is even, and $x_{n+1}= \frac{x_n+2x_{n-1}+q}{2}$ if $x_n$ is odd. A $1$ -cycle is a periodic sequence with one transition from odd to even numbers. We prove theoretical and computational results for the existence of $1$ -cycles, and discuss a generalization to more complex cycles.

Determinantal and permanental representations of companion sequences associated to the r-Fibonacci sequence
Original research paper. Pages 64–74
Hacène Belbachir and Ihab-Eddine Djellas
Full paper (PDF, 181 Kb) | Abstract

Recently companion sequences of r-Fibonacci sequence were defined. The aim of this paper is to give some determinantal and permanental representations of these sequences via Hessenberg matrices. Several representations of classical sequences and polynomials are established. We conclude by using our representations to give n consecutive terms of companion sequences simultaneously.

Two theorems on square numbers
Original research paper. Pages 75–80
Nguyen Xuan Tho
Full paper (PDF, 171 Kb) | Abstract

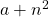
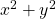
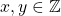
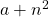
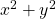
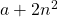
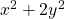
We show that if $a$ is a positive integer such that for each positive integer $n$ , $a+n^2$ can be expressed $x^2+y^2$ , where $x,y\in \mathbb{Z}$ , then $a$ is a square number. A similar theorem also holds if $a+n^2$ and $x^2+y^2$ are replaced by $a+2n^2$ and $x^2+2y^2$ , respectively.

Set partitions with isolated successions
Original research paper. Pages 81–91
Toufik Mansour and Augustine O. Munagi
Full paper (PDF, 232 Kb) | Abstract

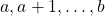
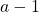
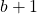
We enumerate partitions of the set $\{1,\dots,n\}$ according to occurrences of isolated successions, that is, integer strings $a,a+1,\dots,b$ in a block when neither $a-1$ nor $b+1$ lies in the same block. Our results include explicit formulas and generating functions for the number of partitions containing isolated successions of a given length.
We also consider a corresponding analog of the associated Stirling numbers of the second kind.

Sums involving generalized harmonic and Daehee numbers
Original research paper. Pages 92–99
Neşe Ömür and Sibel Koparal
Full paper (PDF, 193 Kb) | Abstract

In this paper, we establish some sums involving generalized harmonic and Daehee numbers which are derived from the generating functions. For example, for $n, r\geq 1,$

$\begin{eqnarray*} \sum_{i=0}^{n}H\left( i,r-1,\alpha \right) H_{n-i}^{r}\left( \alpha \right) &=&\sum_{l_{1}+l_{2}+ \cdots +l_{r+1}=n}H_{l_{1}}(\alpha )H_{l_{2}}(\alpha ) \cdots H_{l_{r+1}}(\alpha ). \end{eqnarray*}$

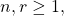
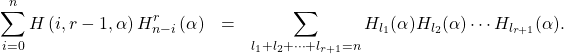
Partitions with k sizes from a set
Original research paper. Pages 100–108
A. David Christopher
Full paper (PDF, 202 Kb) | Abstract

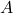
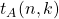
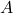
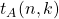
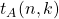
Let $n$ and $k$ be two positive integers and let $A$ be a set of positive integers. We define $t_A(n,k)$ to be the number of partitions of $n$ with exactly $k$ sizes and parts in $A$ . As an implication of a variant of Newton’s product-sum identities we present a generating function for $t_A(n,k)$ . Subsequently, we obtain a recurrence relation for $t_A(n,k)$ and a divisor-sum expression for $t_A(n,2)$ . 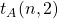Also, we present a bijective proof for the latter expression.

A note on generalized and extended Leonardo sequences
Original research paper. Pages 109–114
Anthony G. Shannon and Ömür Deveci
Full paper (PDF, 605 Kb) | Abstract

This note considers some real and complex extensions and generalizations of the Leonardo sequence, which is embedded within each of these two types of intriguing sequences, intriguing because there are still some unanswered questions. The connections between inhomogeneous and homogeneous forms are used as examples of a possible reason that the Leonardo sequences have been, in a sense, historically neglected.

Leonardo’s bivariate and complex polynomials
Original research paper. Pages 115–123
Milena Carolina dos Santos Mangueira, Renata Passos Machado Vieira, Francisco Regis Vieira Alves and Paula Maria Machado Cruz Catarino
Full paper (PDF, 225 Kb) | Abstract

Given the purpose of mathematical evolution of Leonardo’s sequence, we have the prospect of introducing complex polynomials, bivariate polynomials and bivariate polynomials around these numbers. Thus, this article portrays in detail the insertion of the variable x, y and the imaginary unit i in the sequence of Leonardo. Nevertheless, the mathematical results from this process of complexification of these numbers are studied, correlating the mathematical evolution of that sequence.

On certain inequalities for the prime counting function – Part II
Original research paper. Pages 124–128
József Sándor
Full paper (PDF, 149 Kb) | Abstract

As a continuation of [6], we deduce some inequalities of a new type for the prime counting function π(x).

Linear recurrence sequence associated to rays of negatively extended Pascal triangle
Original research paper. Pages 129–142
Hacène Belbachir, Abdelkader Bouyakoub and Fariza Krim
Full paper (PDF, 247 Kb) | Abstract

We consider the extension of generalized arithmetic triangle to negative values of rows and we describe the recurrence relation associated to the sum of diagonal elements laying along finite rays. We also give the corresponding generating function. We conclude by an application to Fibonacci numbers and Morgan-Voyce polynomials with negative subscripts.

On two new combined 3-Fibonacci sequences. Part 3
Original research paper. Pages 143–146
Krassimir T. Atanassov
Full paper (PDF, 122 Kb) | Abstract

Two new combined 3-Fibonacci sequences are introduced and the explicit formulae for their n-th members are given.

This issue of the International Journal “Notes on Number Theory and Discrete Mathematics” is published with the financial support of the Bulgarian National Science Fund, Grant Ref. No. KP-06-NP3/43/2021.

Volume 28 ▶ Number 1 ▷ Number 2 ▷ Number 3 ▷ Number 4

Latest Issue

Journal Contents