Sums involving generalized harmonic and Daehee numbers

Neşe Ömür and Sibel Koparal
Notes on Number Theory and Discrete Mathematics
Print ISSN 1310–5132, Online ISSN 2367–8275
Volume 28, 2022, Number 1, Pages 92–99
DOI: 10.7546/nntdm.2022.28.1.92-99
Full paper (PDF, 193 Kb)

Details

Authors and affiliations

Neşe Ömür
Department of Mathematics, University of Kocaeli
41380 Izmit, Kocaeli, Turkey

Sibel Koparal
Department of Mathematics, University of Bursa Uludağ
16059 Nilüfer, Bursa, Turkey

Abstract

In this paper, we establish some sums involving generalized harmonic and Daehee numbers which are derived from the generating functions. For example, for n, r\geq 1,

    \begin{eqnarray*} \sum_{i=0}^{n}H\left( i,r-1,\alpha \right) H_{n-i}^{r}\left( \alpha \right) &=&\sum_{l_{1}+l_{2}+ \cdots +l_{r+1}=n}H_{l_{1}}(\alpha )H_{l_{2}}(\alpha ) \cdots H_{l_{r+1}}(\alpha ). \end{eqnarray*}

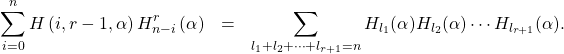
Keywords

  • Sums
  • Generalized harmonic numbers
  • Daehee numbers

2020 Mathematics Subject Classification

  • 05A15
  • 05A19
  • 11B73

References

  1. Benjamin, A. T., Gaebler, D., & Gaebler, R. (2013). A combinatorial approach to
    hyperharmonic numbers. The Electronic Journal of Combinatorial Number Theory, 3, 1–9.
  2. Benjamin, A. T., Preston, G. O., & Quinn, J. J. (2002). A Stirling encounter with harmonic numbers. Mathematics Magazine, 75, 95–103.
  3. Caralambides, C. A. (2002). Enumarative Combinatorics. New York: Chapman and Hall/Crc.
  4. Cheon, G.-S., & El-Mikkawy, M. (2008). Generalized harmonic numbers with Riordan arrays. Journal of Number Theory, 128(2), 413–425.
  5. Comtet, L. (1974). Advanced Combinatorics, D. Reidel Publishing Company,
    Dordrecht-Holland, Boston-U.S.A.
  6. Dattoli, G., Licciardi, S., Sabia, E., & Srivastava, H. M. (2019). Some properties and generating functions of generalized harmonic numbers. Mathematics, 7(7), Article 577.
  7. Dattoli, G., & Srivastava, H. M. (2008). A note on harmonic numbers, umbral calculus and generating functions. Applied Mathematics Letters, 21(7), 686–693.
  8. Duran, O., Ömür , N. & Koparal, S. (2020). On sums with generalized harmonic,
    hyperharmonic and special numbers. Miskolc Mathematical Notes, 21(2), 791–803.
  9. Genčev, M. (2011). Binomial sums involving harmonic numbers. Mathematica Slovaca, 61(2), 215–226.
  10. Jang, L.-C., Kim, W., Kwon, H.-I., & Kim, T. (2020). On degenerate Daehee polynomials and numbers of the third kind. Journal of Computational and Applied Mathematics, 364, Article 112343.
  11. Kim, D. S., & Kim, T. (2013). Identities involving harmonic and hyperharmonic numbers. Advances in Difference Equations, 2013, Article 235.
  12. Kim, T., & Kim, D. S. (2020). Some Relations of Two Type 2 Polynomials and Discrete Harmonic Numbers and Polynomials. Symmetry, 12(6), Article 905.
  13. Kim, T., Kim, D. S., Kim, H. Y., & Kwon, J. (2020). Some results on degenerate Daehee and Bernoulli numbers and polynomials. Advances in Difference Equations, 2020, Article 311.
  14. Kim, T., Kim, D. S., Kwon, J., & Park, S.-H. (2022). Representation by Degenerate Genocchi Polynomials. Journal of Mathematics, 2022, Article 2339851.
  15. Ömür, N., & Bilgin, G. (2018). Some applications of the generalized hyperharmonic numbers of order r, 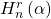H_{n}^{r}\left( \alpha \right). Advances and Applications in Mathematical Sciences, 17(9), 617–627.
  16. Ömür, N., & Koparal, S. (2018). On the matrices with the generalized hyperharmonic numbers of order r. Asian-European Journal of Mathematics, 11(3), Article 1850045.
  17. Rim, S.-H., Kim, T., & Pyo, S.-S. (2018). Identities between harmonic, hyperharmonic and Daehee numbers. Journal of Inequalities and Applications, 2018, Article 168.
  18. Santmyer, J. M. (1997) A Stirling like sequence of rational numbers. Discrete Mathematics, 171(1-3), 229–235.
  19. Simsek, Y. (2014). Special numbers on analytic functions. Applied Mathematics, 5(7), 1091–1098.
  20. Sofo, A., & Srivastava, H. M. (2011). Identities for the harmonic numbers and binomial coefficients. The Ramanujan Journal, 25(1), 93–113.

Manuscript history

  • Received: 24 January 2021
  • Revised: 11 February 2021
  • Accepted: 16 February 2022
  • Online First: 17 February 2022

Related papers

Cite this paper

Ömür, N., & Koparal, S. (2022). Sums involving generalized harmonic and Daehee numbers. Notes on Number Theory and Discrete Mathematics, 28(1), 92-99, DOI: 10.7546/nntdm.2022.28.1.92-99.

Comments are closed.